Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 3
Travailler ensemble
Message de Léonard de Vinci
9 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les parties de cet exercice sont indépendantes et chacune d'entre elles peut être réalisée seul(e) ou en groupe. Les élèves mettent leurs résultats en commun pour résoudre le problème.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Léonard de Vinci a laissé plusieurs citations célèbres et l'une d'elles semble tout particulièrement destinée aux élèves du cours de mathématiques. Elle a été cryptée avec un code de César.
L'objectif de cet exercice est de trouver la clé de codage puis de déchiffrer cette phrase. Cette clé sera trouvée grâce à un trinôme dont il faut obtenir les trois coefficients.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Partie 1
1. Vérifier que \dfrac{-1}{2} est une racine de \text{P}.
2. On admet que \text{P} est factorisable par \left(x+\dfrac{1}{2}\right).
Déterminer trois réels a , b et c tels que \mathrm{P}(x)=\left(x+\dfrac{1}{2}\right)\left(a x^{2}+b x+c\right) pour tout x réel.
2. On admet que \text{P} est factorisable par \left(x+\dfrac{1}{2}\right).
Déterminer trois réels a , b et c tels que \mathrm{P}(x)=\left(x+\dfrac{1}{2}\right)\left(a x^{2}+b x+c\right) pour tout x réel.
3. Déterminer toutes les racines de \text{P}.
4. En déduire le coefficient demandé.
4. En déduire le coefficient demandé.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Partie 2
Soit f le trinôme défini sur \R par f(x)=3 x^{2}+5 x-2.
Soit g le trinôme défini sur \R par g(x)=2 x^{2}-x-10.
Un des coefficients du trinôme qui donnera la clé de codage est le plus petit entier naturel d'un intervalle sur lequel f et g sont positives toutes les deux.
Retrouver ce nombre en étudiant le signe de ces fonctions.
Retrouver ce nombre en étudiant le signe de ces fonctions.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Partie 3
f est une fonction trinôme vérifiant :
f(1)=18 \: ;
f(-1)=2 \: ;
\Delta=160.
Un des coefficients du trinôme qui donnera la clé de codage est l'ordonnée du sommet de la parabole \mathcal { P } représentant la fonction f. Cette ordonnée est un nombre entier.
Déterminer f à l'aide des indications ci-dessus et d'un système, puis déterminer le coefficient demandé.
\Delta=160.
Un des coefficients du trinôme qui donnera la clé de codage est l'ordonnée du sommet de la parabole \mathcal { P } représentant la fonction f. Cette ordonnée est un nombre entier.
Déterminer f à l'aide des indications ci-dessus et d'un système, puis déterminer le coefficient demandé.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Mise en commun
Le trinôme recherché est de la forme a x^{2}+b x+c où c est la solution de la partie 1, a est la solution de la partie 2 et b est la solution de la partie 3.
1. Écrire l'expression du trinôme recherché.2. La différence entre la somme et le produit des racines de ce trinôme est la clé permettant de décoder le message de Léonard de Vinci. Décoder le message.
Le zoom est accessible dans la version Premium.
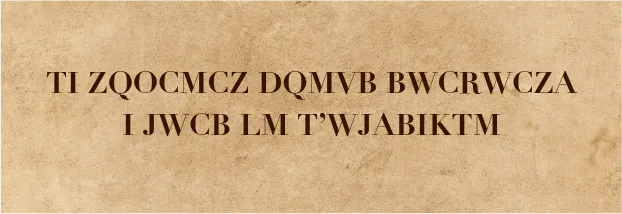
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
À l'aide de Python, effectuer un programme permettant de déchiffrer un message avec un code de César lorsque la clé est connue.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah