Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 2
Cours 1
Fonction valeur absolue
16 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
En seconde, la valeur absolue d'un nombre réel et la distance entre deux réels ont été
étudiées.
Ces notions permettent de définir une nouvelle fonction.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ADéfinition et courbe représentative
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
La fonction valeur absolue est définie sur \mathbb { R } par f ( x ) = | x | .
On a f ( x ) = \left\{ \begin{array} { l l l } { - x } \hspace*{0.2cm} { \text { si } } \hspace*{0.2cm} { x \lt 0 } \\ { x } \hspace*{0.5cm} { \text { si } } \hspace*{0.2cm} { x \geqslant 0 } \end{array} \right.
Sa courbe représentative est donnée dans le graphique suivant.
On a f ( x ) = \left\{ \begin{array} { l l l } { - x } \hspace*{0.2cm} { \text { si } } \hspace*{0.2cm} { x \lt 0 } \\ { x } \hspace*{0.5cm} { \text { si } } \hspace*{0.2cm} { x \geqslant 0 } \end{array} \right.
Sa courbe représentative est donnée dans le graphique suivant.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour tout réel x , on a \sqrt { x ^ { 2 } } = | x | et pour tout réel x \geqslant 0, ( \sqrt { x } ) ^ { 2 } = x.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La fonction valeur absolue est une fonction affine par morceaux.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
La fonction valeur absolue est paire.
Sa représentation graphique est symétrique par rapport à l'axe des ordonnées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une fonction f est paire lorsque son ensemble de définition \mathcal { D } est symétrique par rapport à 0 et que, pour tout réel x \in \mathcal { D }, f(-x) = f(x).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
Pour tout réel x , on a : f ( - x ) = | - x | = | x | = f ( x ). f est donc bien une fonction paire et sa représentation graphique est symétrique par rapport à l'axe des ordonnées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
En utilisant la représentation graphique de la fonction valeur absolue, résoudre l'équation et les inéquations suivantes.
1. | x | = 3
2. | x | \lt 3
3. | x | \gt 3
1. | x | = 3
2. | x | \lt 3
3. | x | \gt 3
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On trace la courbe représentative \text{C} de la fonction valeur absolue et on trace la droite d d'équation y = 3 .
1. Il suffit de lire les deux antécédents du nombre 3.
2. On lit les abscisses des points de \text{C} situés strictement en dessous de d .
3. On lit les abscisses des points de \text{C} situés strictement au-dessus de d .
1. Il suffit de lire les deux antécédents du nombre 3.
2. On lit les abscisses des points de \text{C} situés strictement en dessous de d .
3. On lit les abscisses des points de \text{C} situés strictement au-dessus de d .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
1. Par lecture graphique, on obtient : x = -3 ou x = 3 .
2. Par lecture graphique, on obtient -3 \lt x \lt 3 donc l'ensemble des solutions est ] - 3 \: ; 3[ .
3. Par lecture graphique, on obtient : x \lt -3 ou x \gt 3 .
L'ensemble des solutions est donc ] - \infty \: ; - 3 [ \cup ] 3 \: ; + \infty [.
2. Par lecture graphique, on obtient -3 \lt x \lt 3 donc l'ensemble des solutions est ] - 3 \: ; 3[ .
3. Par lecture graphique, on obtient : x \lt -3 ou x \gt 3 .
L'ensemble des solutions est donc ] - \infty \: ; - 3 [ \cup ] 3 \: ; + \infty [.
Pour s'entraîner
Exercices et p. 59
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BSens de variation et extremum
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
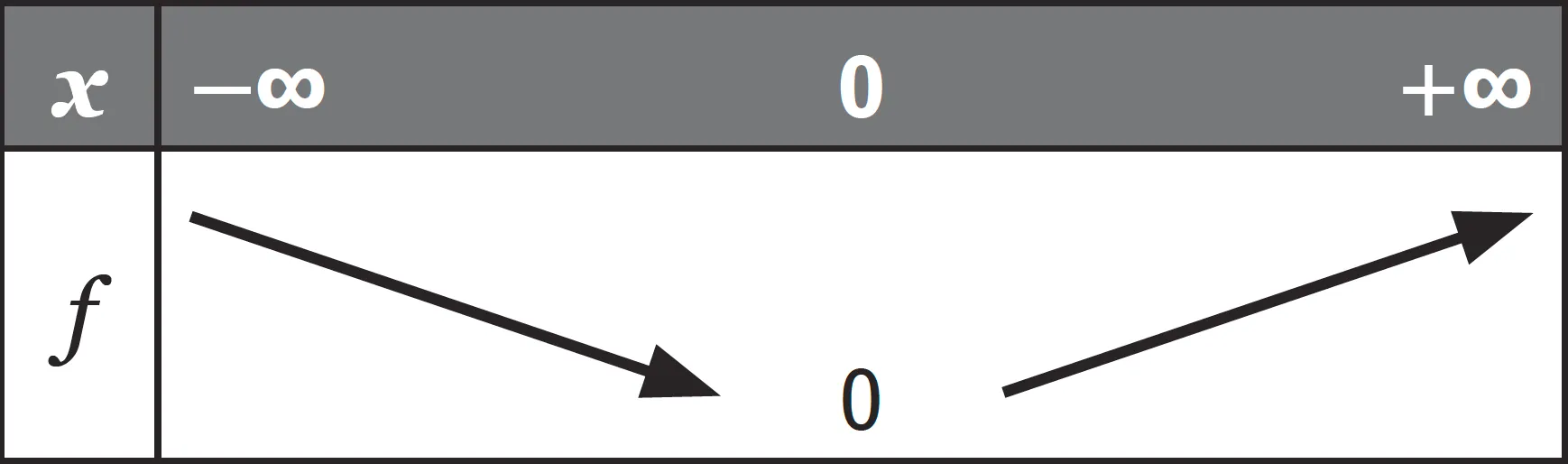
Propriété
La fonction valeur absolue f est strictement décroissante sur ] - \infty \: ; 0 ] et strictement croissante sur [ 0 \: ; + \infty [.
Son minimum sur \mathbb { R } est 0 et il est atteint pour x = 0 .
Son minimum sur \mathbb { R } est 0 et il est atteint pour x = 0 .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
- Sur ] - \infty \: ; 0 ], f est définie par f(x) = -x . f est décroissante sur ] - \infty \: ; 0 ], puisque son coefficient directeur m = -1 est négatif.
- Sur [ 0 \: ; + \infty [, f est définie par f(x) = x donc f est croissante sur [ 0 \: ; + \infty [.
- Pour tout réel x , on a f ( x ) = | x | et | x | \geqslant 0. De plus, f(0) = 0 .
f admet 0 pour minimum sur \mathbb{R}, atteint au point d'abscisse 0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On peut également déduire les variations de f sur [ 0 \: ; + \infty [ en utilisant la symétrie de f par rapport à l'axe des ordonnées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
1. On considère un réel x tel que 2 \leqslant x \lt 5. Déterminer un encadrement de 2 - 3 | x |.
2. On considère un réel x tel que -2 \leqslant x \lt 1. Déterminer un encadrement de 5 | x |-3.
2. On considère un réel x tel que -2 \leqslant x \lt 1. Déterminer un encadrement de 5 | x |-3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
1. On a : 2 \leqslant x \lt 5.
La fonction valeur absolue est croissante sur [ 0 \: ; + \infty [ donc :
\begin{array} { l } { 2 \leqslant | x | \lt 5 } \\ { \Leftrightarrow - 6 \geqslant - 3 | x | \gt - 15 } \\ { \Leftrightarrow - 4 \geqslant 2 - 3 | x | \gt - 13. } \end{array}
On obtient donc l'encadrement - 4 \geqslant 2 - 3 | x | \gt - 13.
2. On a : -2 \leqslant x \lt 1.
La fonction valeur absolue n'étant pas monotone sur [ - 2 \: ; 1 ], on dresse son tableau de variations sur [ - 2 \: ; 1 ].
La fonction valeur absolue est croissante sur [ 0 \: ; + \infty [ donc :
\begin{array} { l } { 2 \leqslant | x | \lt 5 } \\ { \Leftrightarrow - 6 \geqslant - 3 | x | \gt - 15 } \\ { \Leftrightarrow - 4 \geqslant 2 - 3 | x | \gt - 13. } \end{array}
On obtient donc l'encadrement - 4 \geqslant 2 - 3 | x | \gt - 13.
2. On a : -2 \leqslant x \lt 1.
La fonction valeur absolue n'étant pas monotone sur [ - 2 \: ; 1 ], on dresse son tableau de variations sur [ - 2 \: ; 1 ].
Le zoom est accessible dans la version Premium.
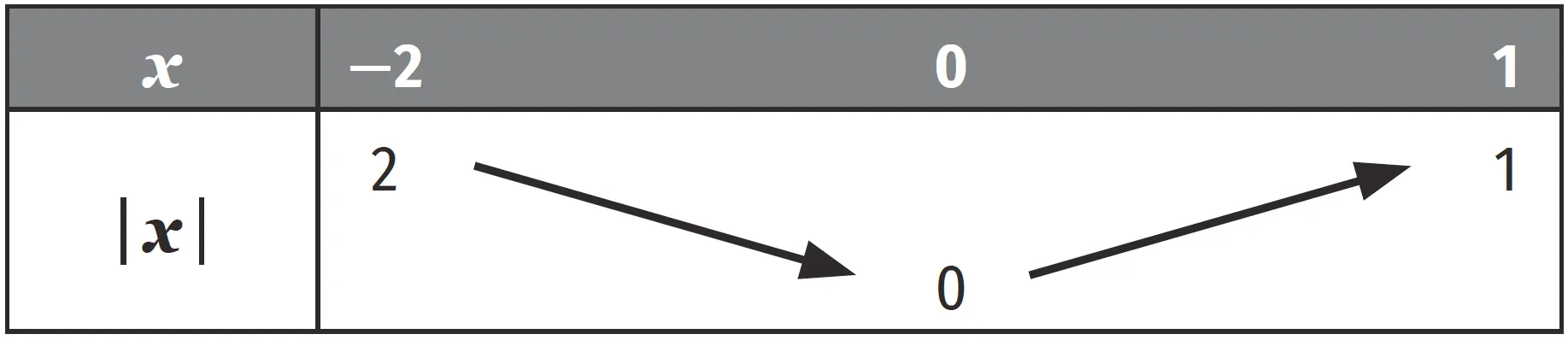
D'où :
\begin{array} { l } { 0 \leqslant | x | \leqslant 2 } \\ { \Leftrightarrow 0 \leqslant 5 | x | \leqslant 10 } \\ { \Leftrightarrow - 3 \leqslant 5 | x | - 3 \leqslant 7 } \end{array}
On obtient donc l'encadrement - 3 \leqslant 5 | x | - 3 \leqslant 7.
Pour s'entraîner
Exercices et p. 61.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- On encadre ce qu'il y a dans la valeur absolue.
- On utilise les variations de la fonction valeur absolue. Attention, il pourra être nécessaire de dresser son tableau de variations (lorsque celle-ci n'est pas monotone sur l'intervalle étudié).
- On termine avec les propriétés opératoires sur les inégalités.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah