1. Transformer une expression en utilisant les propriétés algébriques de la fonction exponentielle.
2. Étudier le comportement de fonctions faisant intervenir la fonction exponentielle.
3. Résoudre des équations et inéquations faisant intervenir la fonction exponentielle.
4. Modéliser une situation à l'aide de la fonction exponentielle.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

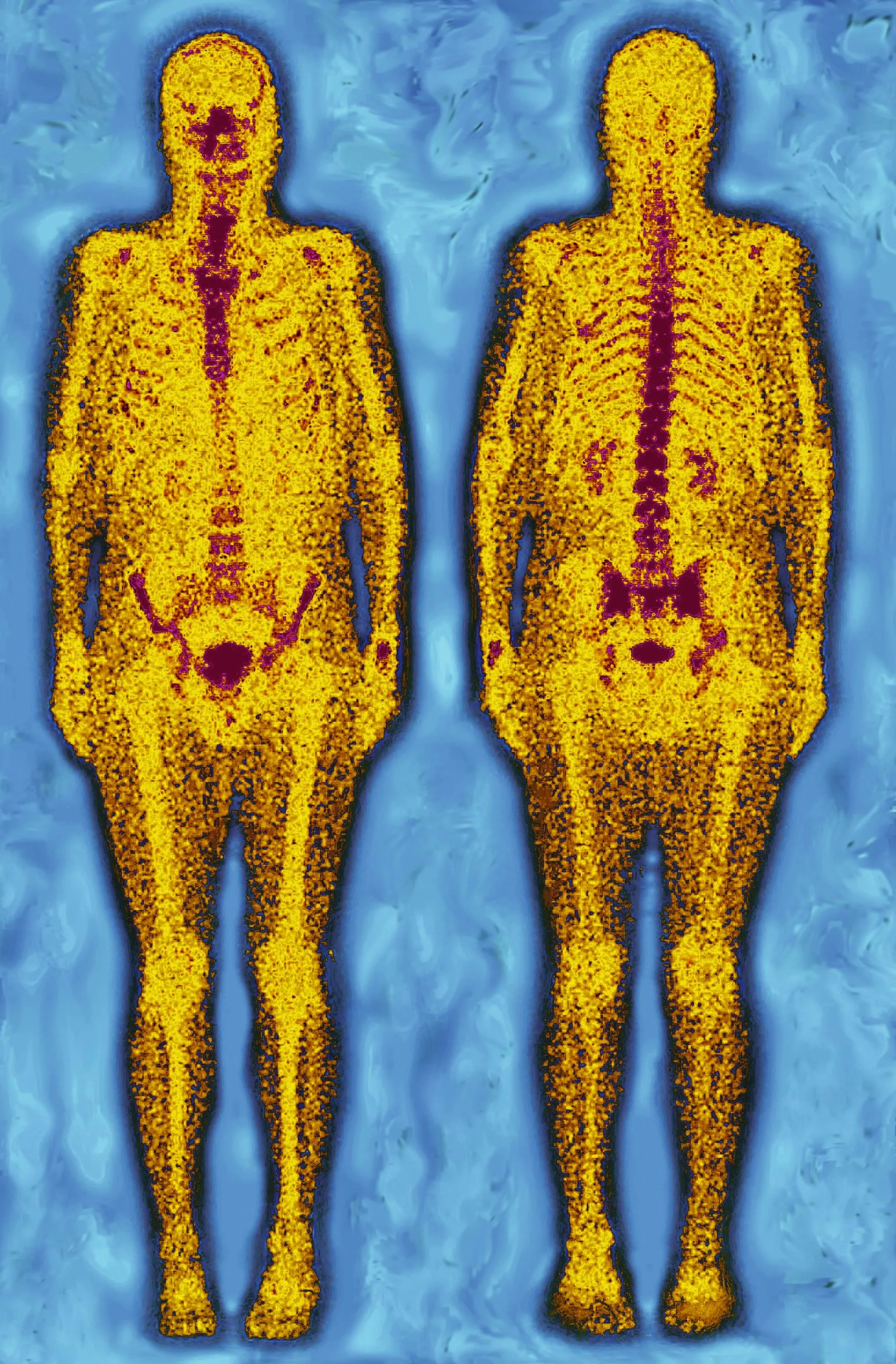
La scintigraphie est une technique d'imagerie médicale qui utilise des substances radioactives. Des isotopes radioactifs sont injectés et vont se fixer sur l'organe ou sur les tissus à explorer en émettant des rayonnements qui seront vus par une caméra spéciale. Grâce à la fonction exponentielle, les médecins connaissent la durée de vie des isotopes radioactifs injectés.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Avant de commencer

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Prérequis

1. Effectuer des calculs numériques simples impliquant des puissances.
2. Établir le tableau de signes d'une expression littérale.
3. Calculer une fonction dérivée en utilisant les opérations usuelles.
4. Utiliser la dérivation pour étudier les variations d'une fonction.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Anecdote

Si vous possédez 1 centime d'euro et que vous doublez votre capital chaque jour, il vous faudra 27 jours pour devenir millionnaire et 37 jours pour devenir milliardaire.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1
Utiliser les puissances

Écrire les expressions suivantes à l'aide d'une seule puissance. 1. 2^{4} \times 2^{7} \times 2^{3}

2. 6^{4} \times 6^{-9}

3. 3^{2} \times 9^{4}

4. 2^{5} \times 3^{5}

5. \dfrac{2^{8} \times 2^{-4}}{2^{-1} \times 2^{3}}

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

2
Utiliser les tangentes à une courbe

On considère une fonction f , définie et dérivable sur \mathbb{R} dont une portion de la courbe représentative est donnée ici. La tangente à la courbe en x = 1 est horizontale. On a, de plus, tracé en vert la tangente à la courbe en x = 0 .

1. Lire graphiquement f'(0).

2. Déterminer la valeur de f'(1) grâce aux données de l'énoncé.

3. Déterminer le signe de f'(-3), f'(-1) et f'(2).

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

3
Déterminer les variations d'une fonction

On considère une fonction g définie et dérivable sur \mathbb{R} dont la dérivée g' est définie par g^{\prime}(x)=(-2 x+6)(3 x+12). Construire le tableau de variations de la fonction g sur \mathbb{R}.

Cliquez pour accéder à une zone de dessin

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

4
Dériver un produit

Soit h la fonction définie par h(x)=x \sqrt{x}.

1. Donner le domaine de définition de h .

2. Sur quel ensemble h est-elle dérivable ?

3. Calculer la fonction dérivée h' de h et déterminer son tableau de signes sur son ensemble de définition.

4. En déduire le tableau de variations de la fonction h .

Cliquez pour accéder à une zone de dessin

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

5
Démontrer avec les dérivées

On considère deux fonctions f et g définies sur le même intervalle \mathrm{I} tel que, pour tout x \in \mathrm{I}, f^{\prime}(x)=g^{\prime}(x) On note h, la fonction définie sur \mathrm{I} par h(x) = f(x) - g(x). 1. Justifier que h est dérivable et déterminer sa fonction dérivée h' .

2. Que peut-on en déduire sur h ?

3. a. Quelle relation algébrique existe-t-il alors entre les fonctions f et g ?

b. En donner une interprétation graphique.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

6
Problème

Une entreprise produit des pièces destinées à l'industrie automobile. On appelle x le nombre de pièces produites en un jour. Pour des raisons matérielles, x \in[0 ; 30]. Le bénéfice journalier de l'entreprise, en euro, peut être modélisé par une fonction \mathrm{B} définie sur [0 ; 30] par \mathrm{B}(x)=-2 x^{2}+60 x-400. 1. Déterminer, pour tout x dans [60\,; 30], l'expression de \mathrm{B}'(x).

2. En déduire la production de l'entreprise permettant de réaliser un bénéfice maximal. Que vaut alors ce bénéfice ?

3. Montrer que \mathrm{B}(x) peut s'écrire sous forme factorisée \mathrm{B}(x)=-2(x-10)(x-20).

4. En déduire les productions pour lesquelles l'entreprise est bénéficiaire.

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Nous préparons votre pageNous vous offrons 5 essais

Yolène

Émilie

Jean-Paul

Fatima

Sarah

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Fonction exponentielle

Avant de commencer

Anecdote

1 Utiliser les puissances

2 Utiliser les tangentes à une courbe

3 Déterminer les variations d'une fonction

4 Dériver un produit

5 Démontrer avec les dérivées

6 Problème

Une erreur sur la page ? Une idée à proposer ?

Nous préparons votre pageNous vous offrons 5 essais

1
Utiliser les puissances

2
Utiliser les tangentes à une courbe

3
Déterminer les variations d'une fonction

4
Dériver un produit

5
Démontrer avec les dérivées

6
Problème