1. a. Tracer, à l'aide de la calculatrice, la parabole d'équation y = 4x^2 + 4x + 5 . En déduire que f est définie sur \R .

b. Vérifier que, pour tout x \in \mathbb { R }, f ^ { \prime } ( x ) = \dfrac { - 2 ( 2 x + 3 ) ( 2 x - 1 ) } { \left( 4 x ^ { 2 } + 4 x + 5 \right) ^ { 2 } }.

c. Étudier le signe de f ^ { \prime } ( x ) sur \R puis dresser le tableau de variations de f .



d. À l'aide de la calculatrice, tracer la courbe \mathcal{C}_f.

2. \text{F} est une fonction définie sur \R ayant pour dérivée la fonction f . On sait, de plus, que \mathrm { F } \left( \dfrac { - 3 } { 2 } \right) = 0.
a. Déterminer une équation de la tangente d à la courbe représentative de \text{F} au point d'abscisse \dfrac { - 3 } { 2 }.

b. Des trois courbes ci-dessous, quelle est celle qui est la représentation de \text{F} ? Justifier.

1. Montrer que, pour tout x \in \mathcal { D } _ { f } , f ( x ) = - x + 3 - \dfrac { 4 } { x - 1 }.

2. \Delta est la droite d'équation y = -x + 3 . Étudier la position relative de \mathcal { C } _ { f } et \Delta.

3. f ^ { \prime } est la fonction dérivée de f sur \mathcal { D } _ { f }. Montrer que, pour tout x \in \mathcal { D } _ { f } , f ^ { \prime } ( x ) = \dfrac { - ( x + 1 ) ( x - 3 ) } { ( x - 1 ) ^ { 2 } }.

4. Étudier le signe de f ^ { \prime } ( x ) en fonction de x \in \mathcal { D } _ { f } puis dresser le tableau de variations de f sur \mathcal { D } _ { f }.

5. Déterminer une équation de la tangente à \mathcal { C } _ { f } au point d'abscisse 2.

6. Peut-on trouver une tangente à \mathcal { C } _ { f } de coefficient directeur égal à -1 \:? Justifier.

7. Dans un repère orthogonal, tracer la courbe \mathcal { C } _ { f } ainsi que la droite \Delta .

8. Dans un repère, tracer la courbe représentative de la fonction h définie sur \mathcal { D } _ { f } par h(x) = | f ( x ) |.

Une entreprise fabrique des rétroviseurs pour voitures. La fonction « coût total » est définie sur \text{I} = [0 \: ; 11] par \text{C}(x) = 0\text{,}3x^3 - 3x^2 + 9x + 6 .
\text{C}(x) est exprimée en millier d'euros et x est le nombre de milliers d'articles fabriqués. Le prix de vente de 1\:000 articles est 8\:025 \:€.
On suppose que chaque article fabriqué est vendu.
La courbe représentative de la fonction \text{C} est représentée ci-dessous dans un repère orthogonal.


1. On note \text{R} la fonction recette, exprimée en millier d'euros, relative à la vente de x milliers d'articles.
a. Expliquer pourquoi \text{R}(x) = 8\text{,}025x .

b. Dans le repère ci-dessus, tracer la courbe représentative de \text{R.}
c. Déterminer graphiquement l'intervalle de production qui permet de réaliser un bénéfice.

d. Déterminer graphiquement la quantité x_0 que l'entreprise doit fabriquer pour réaliser un bénéfice maximal.

2. Le bénéfice réalisé par cette entreprise est donné, en millier d'euros, par la fonction \text{B} définie et dérivable sur \text{I.} On note \text {B}^{\prime} la fonction dérivée de \text{B.}
a. Montrer que, pour tout x \in \mathrm { I }, \mathrm { B } ^ { \prime } ( x ) = - 0\text{,}075 ( 6 x - 1 ) ( 2 x - 13 ).

b. Étudier le signe de \text {B}^{\prime}(x) puis dresser le tableau de variations de \text{B.}



c. Retrouver, à partir du tableau de variations, la valeur de x_0. Justifier.

d. Quel est le montant, en euro, du bénéfice maximal ?

1. Justifier que le coût de production total \text{C}(x) pour x kg de truffes est \text{C}(x) = x^3 - 60x^2 + 975x .

2. Exprimer le bénéfice \text{B}(x) réalisé par le producteur pour x kg de truffes conditionnés et vendus.

3. Déterminer la fonction dérivée \text {B} ^ {\prime} de la fonction \text{B} et montrer que, pour tout x \in ] 0 \:; 45 ], \text {B} ^ {\prime} ( x ) = (-3x + 15)(x - 35).

4. Étudier le signe de \text {B} ^ {\prime} ( x ) puis dresser le tableau de variations de \text{B.}

5. Compléter le tableau de valeurs suivant :


6. Représenter graphiquement la fonction \text{B} dans un repère orthogonal ( \text {O} ; \vec { i } , \vec { j } ).

7. À l'aide du graphique, déterminer pour quelles productions de truffes l'exploitation est bénéficiaire.

8. Pour quelle quantité de truffes le bénéfice du producteur est-il maximal ? Quel est alors ce bénéfice maximal ?

Les deux parties de cet exercice sont indépendantes.
Soit f une fonction définie et dérivable sur \R et f ^ { \prime } sa fonction dérivée. On note \mathcal{C} sa courbe représentative.

Partie A : lecture graphique
1. Déterminer graphiquement en justifiant :
a. f(-3) et f ^ { \prime }(-3) puis f(-1) et f ^ { \prime }(-1) \: ;

b. le signe de f ^ { \prime }(x) sur l'intervalle [-6 \: ; 5].

2. Résoudre graphiquement f(x) \gt 0 puis (f(x) - 2)^2 = 4 sur l'intervalle [-6 \: ; 5].

Partie B : calcul littéral
Soit a et b deux réels. On admet que la fonction f est définie par f ( x ) = \dfrac { 2 \left( x ^ { 2 } + a x + b \right) } { x ^ { 2 } + 2 x + 5 }.

1. Montrer que, pour tout x \in \mathbb { R }, x ^ { 2 } + 2 x + 5 = ( x + 1 ) ^ { 2 } + 4 et justifier alors l'ensemble de définition de f .

2. On sait que la courbe \mathcal{C} passe par le point \text {A} \left( 0 \: ; \dfrac { 2 } { 5 } \right). Montrer que b = 1 .

3. Démontrer que, pour tout x \in \mathbb { R }, f ^ { \prime } ( x ) = \dfrac { ( 4 - 2 a ) x ^ { 2 } + 16 x + 10 a - 4 } { \left( x ^ { 2 } + 2 x + 5 \right) ^ { 2 } }.

4. On sait que la courbe \mathcal{C} admet au point d'abscisse -3 une tangente horizontale. Démontrer que a = -2 .

5. Démontrer que, pour tout x \in \mathbb { R }, f ^ { \prime } ( x ) = \dfrac { 8 ( x + 3 ) ( x - 1 ) } { \left( x ^ { 2 } + 2 x + 5 \right) ^ { 2 } }.

6. En déduire alors le signe de f ^ { \prime } ( x ) puis dresser le tableau de variations de la fonction f .

Une citerne d'eau doit être fabriquée à partir d'une bande d'étain de 8 m de long et de 6 m de large et cela en pliant, de chaque côté, une bande de 2 m de large en faisant un angle \alpha avec l'horizontale.

Le but de l'exercice est de répondre à la question suivante :
« Quel angle a permet de maximiser l'aire de la section transversale et, par conséquent, le volume de la citerne ? »
La section transversale est assimilée à un trapèze isocèle \text{ABCD} tel que \text{AB} = \text{BC} = \text{CD} = 2 m et \text{(AD)} est parallèle à \text{(BC).}
\text{H} est le projeté orthogonale de \text{B} sur \text{(AD).}

1. Expliquer pourquoi \widehat{ \mathrm { BAH }} = \alpha.

2. Montrer que h = 2 \sin ( \alpha ) et que \mathrm { AD } = 2 + 4 \cos ( \alpha ).

3. Montrer que l'aire du trapèze \text{ABCD} est \mathrm { S } ( \alpha ) = 4 \sin ( \alpha ) + 4 \sin ( \alpha ) \cos ( \alpha ).

4. On considère la fonction f définie sur \left[ 0 \: ; \dfrac { \pi } { 2 } \right] par f ( \alpha ) = 4 \sin ( \alpha ) + 4 \sin ( \alpha ) \cos ( \alpha ).
a. Sur GeoGebra et à l'aide de l'instruction Fonction (4 sin(x) + 4 sin(x) cos(x),0 , pi/2), tracer la courbe représentative de la fonction f .

b. La fonction f semble avoir un maximum. Quelle est la valeur de ce maximum ? Pour quelle valeur de x semble-t-il être atteint ?

c. f ^ { \prime } ( x ) est la fonction dérivée de f . Avec GeoGebra, vérifier que f ^ { \prime } ( x ) = 4 \left( 2 \cos ^ { 2 } ( x ) + \cos ( x ) - 1 \right) puis que f ^ { \prime } ( x ) = 8 ( \cos ( x ) + 1 ) ( \cos ( x ) - 0\text{,}5 ).

1. Étudier les variations de f sur \R .

2. Vérifier que f(2) = 0 .

3. Étudier, suivant les valeurs de x , le signe de f(x).

4. \mathcal{C} est la courbe d'équation y = x^3. \Delta est la droite d'équation y = 3x + 2. Étudier la position relative de \mathcal{C} et \Delta.

Une boîte sans couvercle a la forme d'un parallélépipède rectangle. Sa base est un carré de côté x (exprimé en mètre) avec x \gt 0 . Le volume de la boîte est égal à 10\text{ m}^3.
La base est fabriquée à l'aide d'un matériau qui coûte 5 € par mètre carré, tandis que les faces latérales sont construites à l'aide d'un matériau qui coûte 2 € par mètre carré.
On note h la hauteur de la boîte et \text{C} le coût de fabrication d'une boîte.

1. Exprimer h en fonction de x .

2. Montrer que, pour tout x \gt 0 , \text{C} ( x ) = \dfrac { 5 \left( x ^ { 3 } + 16 \right) } { x }.

3. On note \mathrm { C } ^ { \prime } la fonction dérivée de \text{C.} Montrer que, pour tout x \gt 0 , \text{C} ^ { \prime } ( x ) = \dfrac { 10 \left( x ^ { 3 } - 8 \right) } { x ^ { 2 } }.

4. Étudier les variations de la fonction \text{C} puis trouver les dimensions de la boîte pour lesquelles le coût de fabrication est minimal.

Soit h la fonction définie sur \R par h(x) = -9x^4 + x^3 . Maël a représenté cette fonction à la calculatrice pour dresser son tableau de variations.


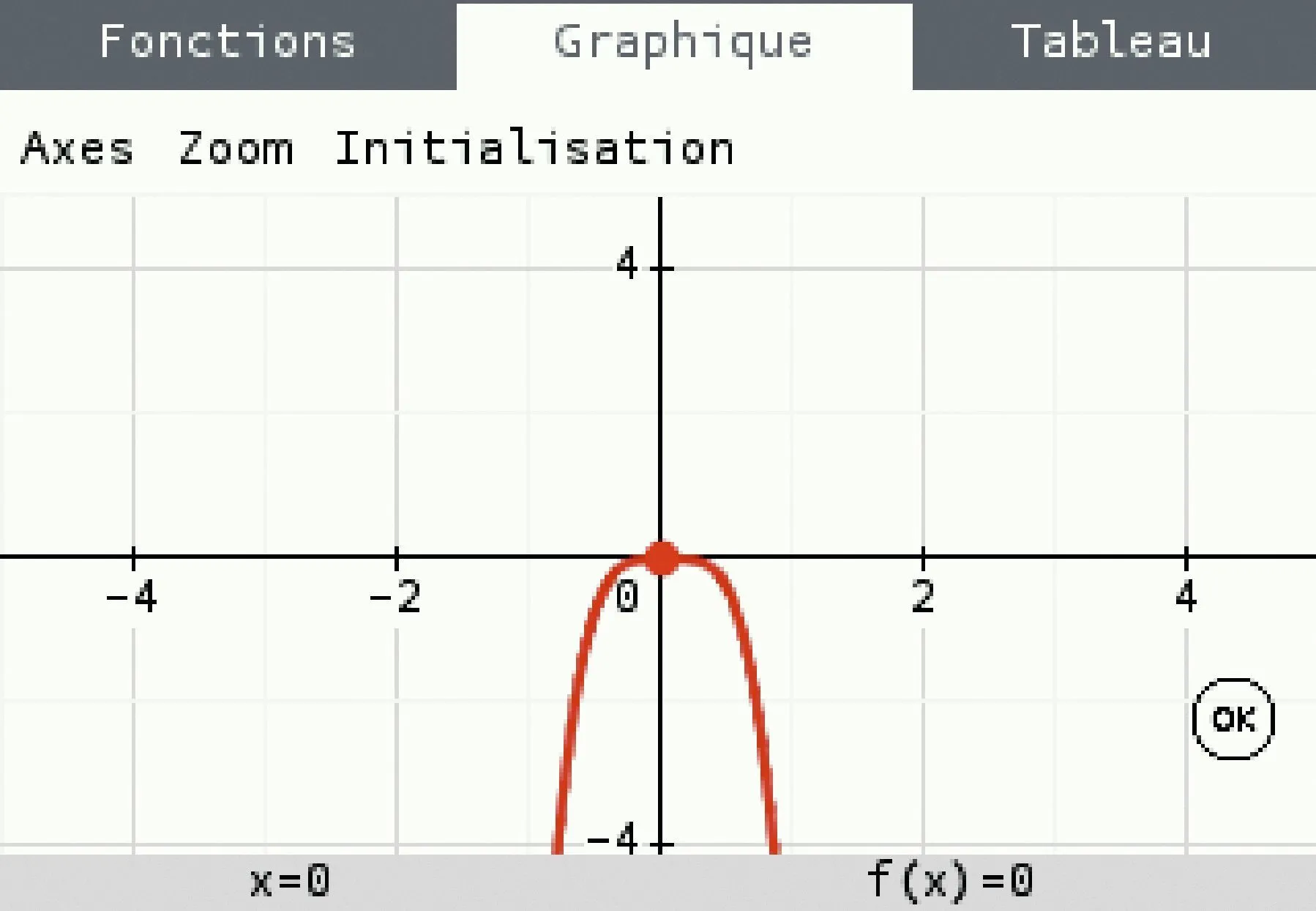
1. À partir de cette représentation, comment dresser le tableau de variations de h \:? h admet-elle un maximum ?

2. On note h ^ { \prime } la fonction dérivée de h sur \R.
a. Déterminer l'expression de h ^ { \prime }(x).

b. En déduire le tableau de variations de h sur \R ainsi que le maximum de h .

3. Proposer à Maël une fenêtre d'affichage permettant de voir les résultats obtenus à la question 2..

Partie A :
g est la fonction définie sur \R par g(x) = x^3 + 3x - 4 .

1. Montrer que la fonction g est strictement croissante sur \R puis dresser son tableau de variations.

2. Calculer g(1) puis conjecturer le signe de g(x) sur \R .

Partie B :
f est la fonction définie sur \R par f ( x ) = \dfrac { - 2 x ^ { 3 } + 4 x ^ { 2 } } { x ^ { 2 } + 1 }.
\mathcal{C}_f est la courbe représentative de f dans un repère orthonormé.

1. Justifier que f est dérivable et montrer que, pour tout x \in \mathbb { R }, f ^ { \prime } ( x ) = \dfrac { - 2 x \times g ( x ) } { \left( x ^ { 2 } + 1 \right) ^ { 2 } }.

2. Étudier le signe de f ^ { \prime } ( x ) puis dresser le tableau de variations de f sur \R .

2. Peut-on trouver des points de \mathcal{C}_f en lesquels la tangente est parallèle à la droite \Delta d'équation y = -2x \: ? Si oui, préciser leurs abscisses respectives.

Fonctions à deux variables :
f est une fonction à deux variables x et y telle que f(x \:; y) = xy(x - y) où x et y sont des entiers qui appartiennent à l'intervalle [0\: ; 10] . On admet que f a un maximum pour des valeurs entières de x et y . Le but de l'algorithme ci-dessous est de trouver le maximum de la fonction f .

\boxed{ \begin{array} { l } { x \leftarrow 0 } \\ y \leftarrow 0 \\ f \leftarrow 0 \\ \text {Pour } x \text { allant de } 0 \text{ à } 10 : \\ \quad \text {Pour } y \text { allant de } 0 \text{ à } 10 : \\ \quad \quad g \leftarrow xy(x-y) \\ \quad \quad \text {Si } g \gt f: \\ \quad \quad \quad f \leftarrow g \\ \quad \quad \text {Fin Si}\\ \quad \text {Fin Pour} \\ \text {Fin Pour} \end{array} }

1. Comparer f(2\: ; 3) et f(3\: ; 2).

2. Quelle est la valeur calculée à la fin de cet algorithme ?

3. Modifier cet algorithme afin qu'il affiche les valeurs de x et y pour lesquelles f atteint son maximum.