Mathématiques 1re Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 5
Applications directes
Exercices d'applications directes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
À l'oral
Envie de réaliser ces exercices à l'oral ? Enregistrez‑vous !
Enregistreur audio
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
14
f est la fonction définie sur ]0\: ; +\infty[ par f( x ) = x ^ { 5 } + 2 \sqrt { x }.
Étudier les variations de f sur ]0\: ; +\infty[.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15
On donne ci-dessous le tableau de signes de
la dérivée g^ { \prime } d'une fonction g définie et dérivable sur \R .
Déterminer les plus grands intervalles sur lesquels g est strictement décroissante.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16
On donne ci-dessous la courbe représentative
d'une fonction h définie et dérivable sur \R.h ^ { \prime } est la fonction dérivée de h .
1. Quel est le signe de h ^ { \prime } ( x ) sur l'intervalle ] - \infty \: ; - 2 ] \: ?
2. Pour quelles valeurs de x , h ^ { \prime } ( x ) s'annule-t-elle?
3. Peut-on dire que h(1) est un extremum local de h \:?
2. Pour quelles valeurs de x , h ^ { \prime } ( x ) s'annule-t-elle?
3. Peut-on dire que h(1) est un extremum local de h \:?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17
On donne ci-dessous le tableau de variations
d'une fonction f définie et dérivable sur [-2\: ; 4].
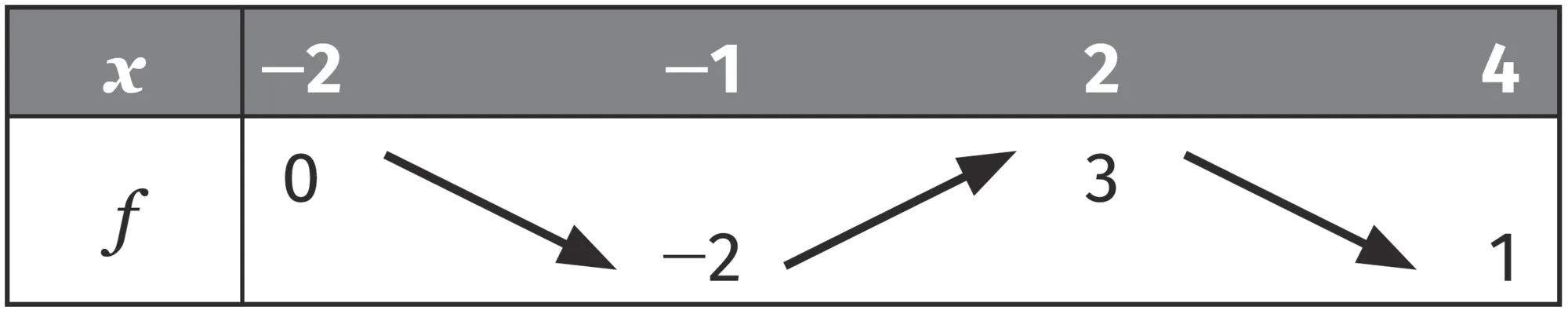
1. Donner, suivant les valeurs de x , le signe de f ^ { \prime } ( x ) sur [-2\: ; 4].
2. Déterminer les extremums locaux de f sur [-2\: ; 4].
2. Déterminer les extremums locaux de f sur [-2\: ; 4].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18
g est une fonction définie et dérivable sur [ - 8\: ; 8 ]. On donne ci-dessous le tableau de variations
de g . g ^ {\prime} est la fonction dérivée de g .
1. Quel est le signe de g ^ {\prime} sur [-8\: ; 0]\: ? sur [0\: ; 1]\: ?
2. Donner un intervalle de nombres positifs sur lequel g ^ {\prime} est positive.
2. Donner un intervalle de nombres positifs sur lequel g ^ {\prime} est positive.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19
f est une fonction définie et dérivable sur \R telle que f ^ { \prime } ( x ) est positif sur \R et f(-1) = 0 .1. Dresser le tableau de variations de f .
Cliquez pour accéder à une zone de dessin
2. Donner, suivant les valeurs de x , le signe de f(x) sur \R .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20
g est une fonction définie et dérivable sur \R telle que g ^ { \prime } ( x ) est positif sur ] - \infty \:; 5 ] et négatif sur [ 5\: ; + \infty [ et g(5) = -1 .1. Dresser le tableau de variations de g .
Cliquez pour accéder à une zone de dessin
2. Quel est le maximum de g sur \R \: ? Quel est le signe de g(x) sur \R \: ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21
h est une fonction définie et dérivable sur [ - 3\: ; 4 ].
h ^ { \prime } est la fonction dérivée de h .La courbe ci-dessous est la courbe représentative de la fonction h ^ { \prime }.
Sachant que h(-1) = 2 et que h(3) = -1 , dresser le tableau de variations de h sur [-3\: ; 4].
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22
f est une fonction définie et dérivable sur [-2\: ; 6]. f ^ { \prime } est la fonction dérivée de f.On donne ci-dessous le tableau de signes de f ^ { \prime }(x).
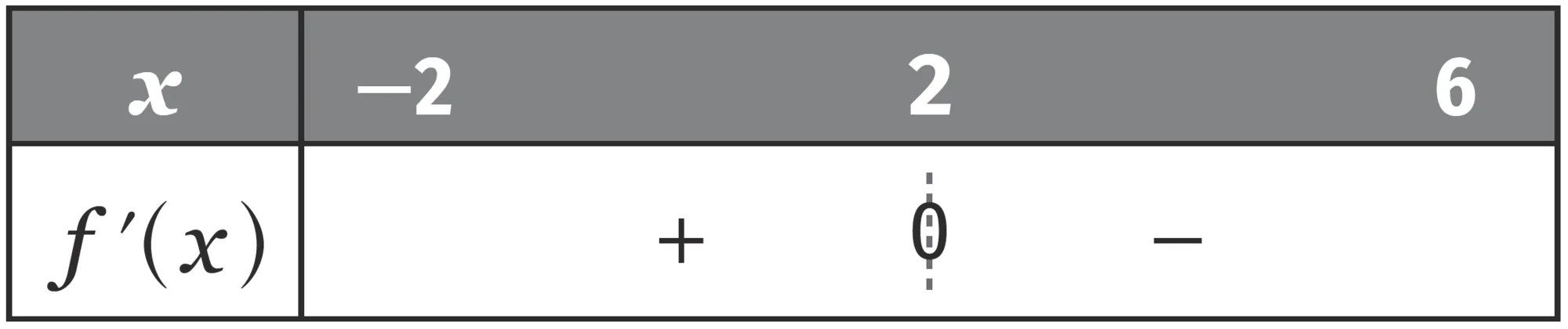
On sait que f(1) = 0 et f(6) = 1 . Dresser le tableau de signes de f(x).
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
g est la fonction définie et dérivable sur \R par g(x) = -x^3 + x^2 + x + 2 .
g ^ { \prime } est la fonction dérivée de g .
À l'aide du logiciel Xcas, on a déterminé g ^ { \prime }(x) ainsi que
sa forme factorisée.
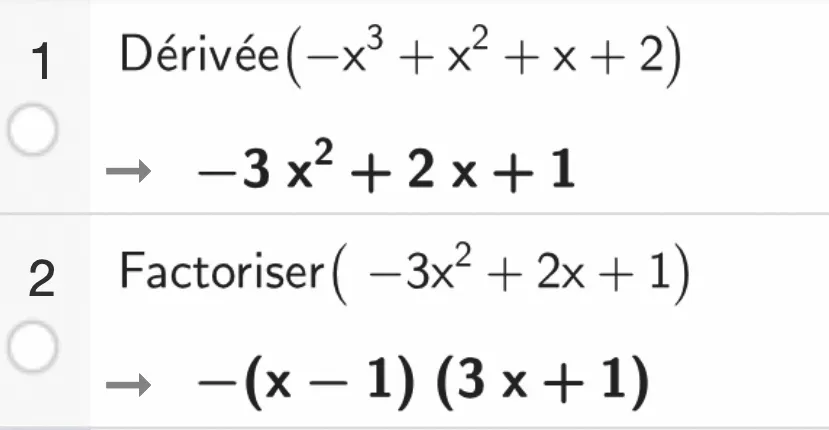
1. Étudier le signe de g ^ { \prime } ( x ) puis dresser le tableau de variations de g .
Cliquez pour accéder à une zone de dessin
2. Calculer g(2) puis dresser le tableau de signes de g(x).
Cliquez pour accéder à une zone de dessin
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
