Chapitre 5
TP / TICE 1
Un ensemble de points
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Le schéma suivant représente une ville, on souhaite relier deux tours \text{T}_1 et \text{T}_2 à la fibre. Les distances sont données en centaine de mètres. On prévoit que
les câbles suivent une structure rectiligne.
Pour différentes raisons, les câbles doivent partir d'un point \text{A} situé le long
de la route entre les points \text{R}_1 et \text{R}_2.
Questions préliminaires :
On note x la distance \text{AR}_1 .
1. À quel intervalle appartient x \: ?
2. Exprimer les longueurs \text{AT}_1 et \text{AT}_2 en fonction de x .
Questions préliminaires :
On note x la distance \text{AR}_1 .
1. À quel intervalle appartient x \: ?
2. Exprimer les longueurs \text{AT}_1 et \text{AT}_2 en fonction de x .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Déterminer la position du point \text{A} et
calculer la longueur totale des deux
structures rectilignes de telle sorte que
cette longueur soit minimale.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1GeoGebra
1. À l'aide d'une fenêtre Calcul formel de GeoGebra,
définir les fonctions f et g puis définir la fonction h par h(x) = f(x) + g(x).

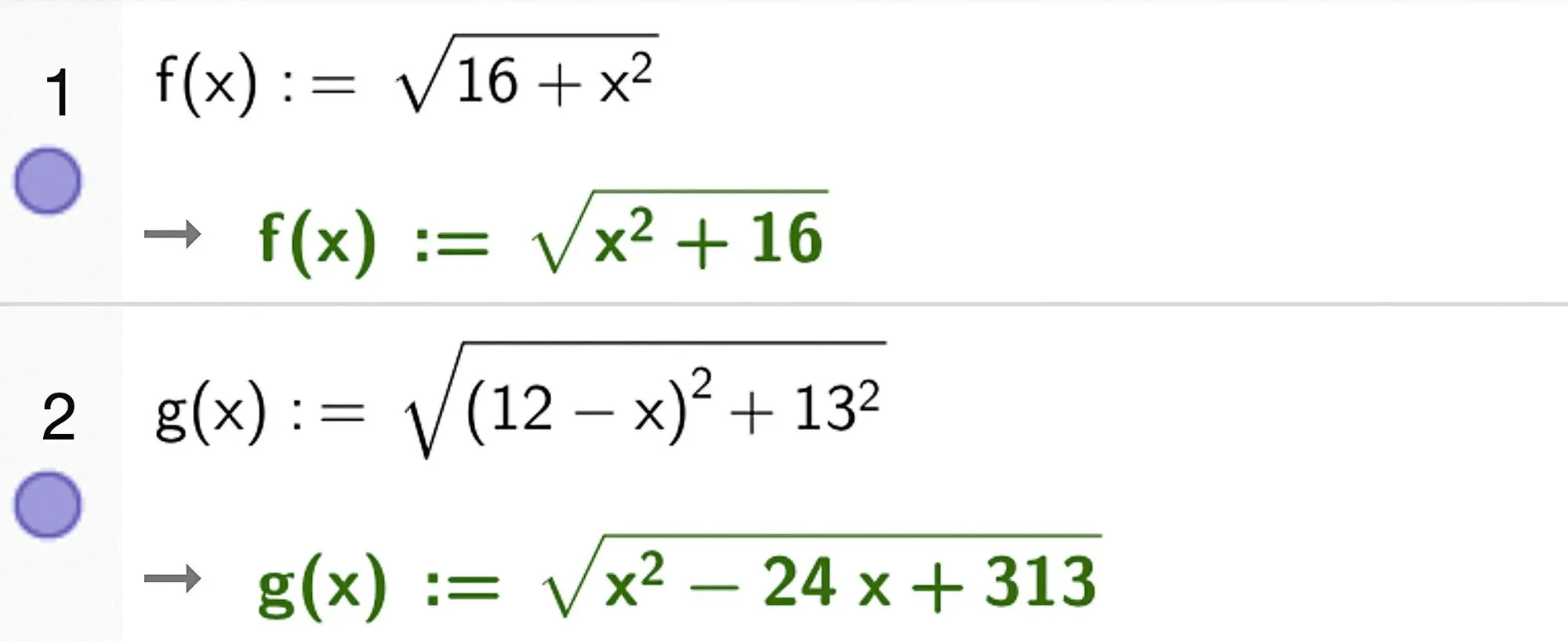
2. Quel est le lien entre l'objectif du TP et la fonction h \: ?
3. Quelle équation faut-il résoudre pour obtenir la valeur de x pour laquelle la fonction h atteint son minimum ?
4. Faire calculer par le logiciel la dérivée de la fonction h et, à l'aide de GeoGebra, résoudre l'équation de la question précédente.

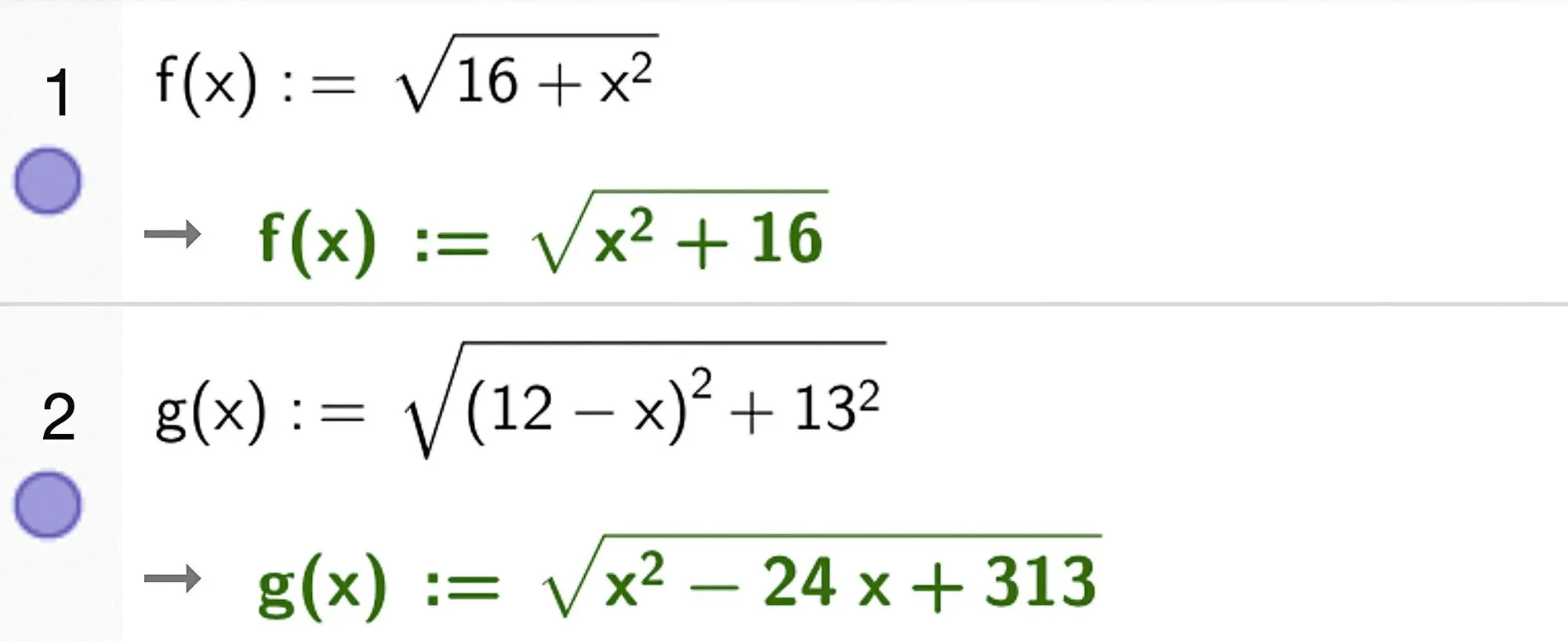
Remarque : La racine carrée peut s'obtenir avec la commande sqrt.
2. Quel est le lien entre l'objectif du TP et la fonction h \: ?
3. Quelle équation faut-il résoudre pour obtenir la valeur de x pour laquelle la fonction h atteint son minimum ?
4. Faire calculer par le logiciel la dérivée de la fonction h et, à l'aide de GeoGebra, résoudre l'équation de la question précédente.
5. Répondre alors au problème en donnant des
valeurs approchées au mètre près.
Vérifier graphiquement les résultats obtenus.
Vérifier graphiquement les résultats obtenus.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Python
1. Définir ces deux fonctions à l'aide de Python.

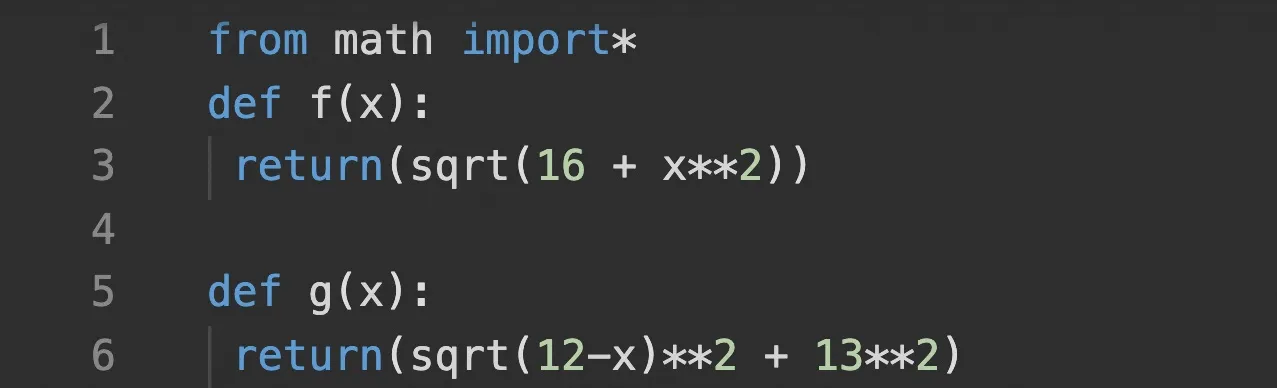
2. On note h la fonction définie sur [0\: ; 12] par h(x) = f(x) + g(x). Quel est le lien entre l'objectif du TP et la fonction h \:?
3. Programmer un algorithme de balayage avec un pas de 0\text{,}1 permettant d'obtenir la valeur de h la plus petite possible.
4. Reprendre la question précédente avec un pas de 0\text{,}01 et répondre à l'objectif posé.


2. On note h la fonction définie sur [0\: ; 12] par h(x) = f(x) + g(x). Quel est le lien entre l'objectif du TP et la fonction h \:?
3. Programmer un algorithme de balayage avec un pas de 0\text{,}1 permettant d'obtenir la valeur de h la plus petite possible.
4. Reprendre la question précédente avec un pas de 0\text{,}01 et répondre à l'objectif posé.
Cliquez pour accéder à la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Une troisième tour \text{T}_3 est positionnée au milieu du segment [\text{T}_1\text{T}_2]. On souhaite également relier cette tour. Où doit alors se situer le point \text{A} pour
que la distance totale des trois structures rectilignes soit minimale ?
2. Lorsque u est une fonction définie et strictement positive sur un intervalle \text{I} à valeurs dans \text{J,} alors la fonction \sqrt { u } est définie et dérivable sur \text{J}
et ( \sqrt { u } ) ^ { \prime } = \dfrac { u ^ { \prime } } { 2 \sqrt { u } }.
En utilisant cette formule, calculer la dérivée de la fonction h définie dans les méthodes de résolution.
En utilisant cette formule, calculer la dérivée de la fonction h définie dans les méthodes de résolution.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

