Nos classiques
Sommaire
Mes pages
N° Page
Algèbre
Analyse
Géométrie
Probabilités et statistiques
Annexes
/ 353
Page précédente
Chapitre 5
Entraînement 2

Extremums d'une fonction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Différenciation
Parcours 1 : exercices
29
;
31
 ;
40
 ;
42
 ;
57
 ;
59
 ;
75
 et
82
Parcours 2 : exercices
33
 ;
39
 ;
47
 ;
63
 ;
68
 ;
77
 ;
79
 ;
85
 et
95
Parcours 3 : exercices
37
 ;
49
 ;
56
 ;
71
 et
89
 ;
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
57
 [Chercher.]

La courbe ci-dessous représente une fonction h définie sur [ - 8 \: ; 6 ].

Extremums d'une fonction


1. Quel est le maximum local de h sur [-8 \: ; - 4] \:?

2. Quel est le minimum local de h sur [-8 \: ; 0] \:?

3. Quel est le maximum h sur [-8 \: ; 6] \:?

4. Quel est le minimum de h au voisinage de 3 \: ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
58
 [Chercher.]
Le tableau de variations ci-dessous est celui d'une fonction f définie et dérivable sur [-3 \:; 5].

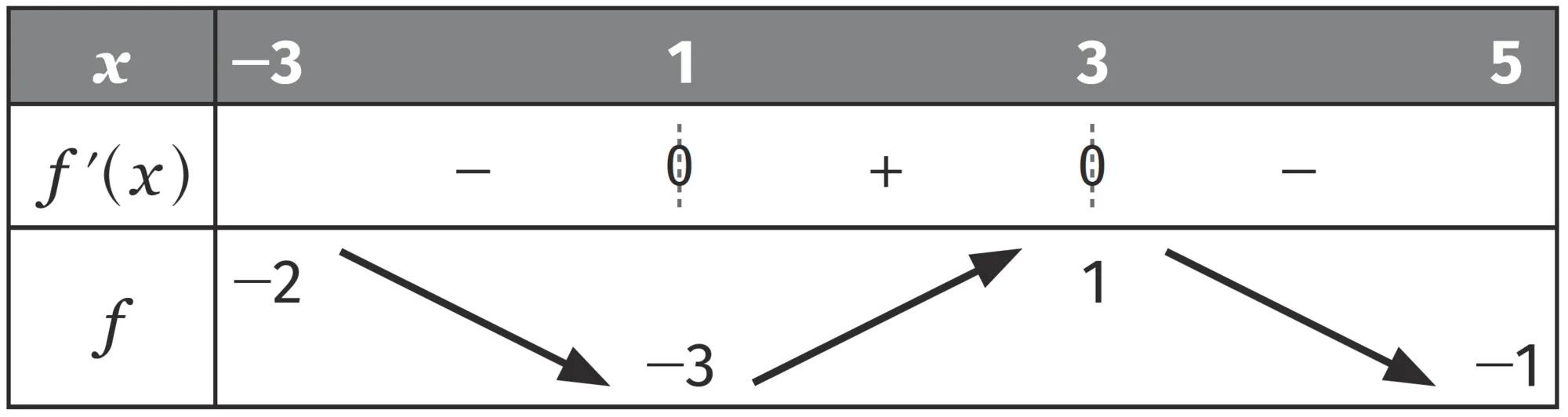
Placeholder pour Tableau variations fonction : valeurs x (-3, 1, 3, 5), signes dérivée f'(x) et valeurs f(x) (-2, -3, 1, -1).Tableau variations fonction : valeurs x (-3, 1, 3, 5), signes dérivée f'(x) et valeurs f(x) (-2, -3, 1, -1).

Déterminer les extremums locaux de f sur [-3 \:; 5].
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Pour les exercices
59
à
63

On suppose que f est une fonction définie et dérivable sur un intervalle donné. Déterminer les éventuels extremums locaux de la fonction f sur cet intervalle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
59
 [Calculer.]

f ( x ) = x ^ { 2 } + 4 x + 3 sur \R.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
60
 [Calculer.]
f ( x ) = \dfrac { 1 } { 4 } x \left( x ^ { 2 } - 12 \right) sur \R.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
61
 [Calculer.]
f ( x ) = 2 x - 3 + \dfrac { 2 } { x - 1 } sur ] 1\: ; + \infty [.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
62
 [Calculer.]
f ( x ) = - x ^ { 3 } + 2 x ^ { 2 } - 2 x + 1 sur \R.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
63
 [Calculer.]

f ( x ) = \dfrac { 3 - x } { x - 2 } sur ] - \infty\: ; 2 [.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Pour les exercices
64
à
66

1. Construire le tableau de variations de f sur son ensemble de définition.
2. Donner, suivant les valeurs de x , le signe de f(x).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
64
 [Chercher.]
f est une fonction définie et dérivable sur \R telle que, pour tout x \in \mathbb { R } , f ^ { \prime } ( x ) > 0 et f ( - 2 ) = 0.

1.
Cliquez pour accéder à une zone de dessin


2.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
65
 [Chercher.]
f est une fonction définie et dérivable sur \R telle que, pour tout x \in ] - \infty \:; 2 [ , f ^ { \prime } ( x ) \gt 0 et, pour tout x \in ] 2\: ; + \infty[ , f ^ { \prime } ( x ) \lt 0 . On sait de plus que f ^ { \prime } ( 2 ) = 0 et f ( 2 ) = - 1.

1.
Cliquez pour accéder à une zone de dessin


2.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
66
 [Chercher.]
f est une fonction définie et dérivable sur \R telle que, pour tout x \in ] - \infty\: ; - 1[, f ^ { \prime } ( x ) \lt 0 et, pour tout x \in ] - 1\: ; + \infty [ , f ^ { \prime } ( x ) \gt 0 .
On sait de plus que f ( - 1 ) = f ^ { \prime } ( - 1 ) = 0.

1.
Cliquez pour accéder à une zone de dessin


2.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
67
 [Chercher.]
f est la fonction définie sur \R par f(x) = x^3 + 5x - 6 .

1. Démontrer que f est strictement croissante sur \R .

2. Vérifier que f(1) = 0 , puis donner le signe de f(x) en fonction des valeurs de x .
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
68
 [Calculer.]

g est la fonction définie sur \R par : g ( x ) = \dfrac { 1 } { 3 } x ^ { 3 } - 2 x ^ { 2 } + 3 x + 1.
1. Vérifier que la dérivée de g sur \R s'annule uniquement pour x = 1 et x = 3.

2. Étudier alors les variations de g sur \R puis dresser son tableau de variations.


Cliquez pour accéder à une zone de dessin


3. Déterminer un encadrement de g(x) sur chacun des intervalles suivants.
a. [0 \: ; 1]

b. [0 \: ; 3]

c. [-1 \: ; 1]

d. [2 \: ; 4]

4. Résoudre, en utilisant le tableau de variations de g , l'inéquation g ( x ) \leqslant g ( 0 ).
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
69
 [Calculer.]
g est la fonction définie sur \R par : g ( x ) = \dfrac { x ^ { 2 } - 3 } { x ^ { 2 } + 1 }.
1. Étudier les variations de g sur \R puis dresser son tableau de variations.


Cliquez pour accéder à une zone de dessin


2. Déterminer un encadrement de g(x) sur chacun des intervalles suivants.
a. [0 \: ; 1]

b. [-1 \: ; 3]

c. [-1 \: ; 1]

d. [ - \sqrt { 3 } \: ; 0 ]

3. Calculer g ( \sqrt { 3 } ) puis résoudre, en utilisant le tableau de variations de g , l'inéquation g ( x ) \leqslant 0.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
70
 [Représenter.]
On donne ci-dessous le tableau de variations d'une fonction f définie sur \mathcal { D } = [ - 3 \:; 0 [ \cup ] 0 \:; 5 ].

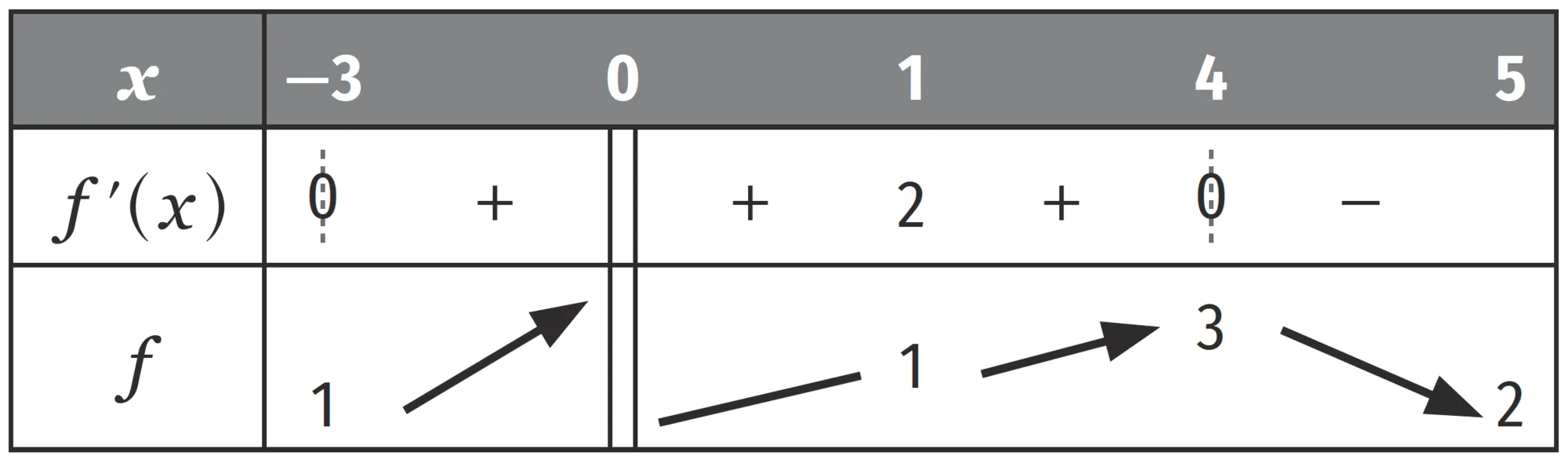
Placeholder pour Tableau variations fonction : valeurs x, f'(x), f. Flèches indiquent variations de f.Tableau variations fonction : valeurs x, f'(x), f. Flèches indiquent variations de f.

1. Écrire une équation pour chacune des tangentes à la courbe représentative de f que le tableau de variations permet de connaître.

2. Donner une courbe compatible avec le tableau de variations de f .

Cliquez pour accéder à une zone de dessin
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
71
 [Chercher.]

f est la fonction définie sur \text{I} = [1 \:; 6] par f ( x ) = a x + b + \dfrac { 8 } { x } où a et b sont des nombres réels.
On admet que f est dérivable sur l'intervalle \text{I} et on note f ^ { \prime } la fonction dérivée de f sur cet intervalle.
La courbe \mathcal{C} ci-dessous représente la fonction f sur \text{I.}

Extremums d'une fonction
1. Déterminer graphiquement f(1), f(2), f(4) et f ^ { \prime } ( 2 ).

2. En déduire les valeurs des réels a et b .

3. On admet que f est définie sur [1 \:; 6] par f ( x ) = 2 x - 10 + \dfrac { 8 } { x }.
a. Justifier la dérivabilité de f sur [1 \: ; 6].

b. Déterminer f ^ { \prime } ( x ) puis étudier les variations de f sur [1 \: ; 6].

c. Dresser le tableau de variations de f en précisant les valeurs de f(1), f(2), f(4) et f(6).

Cliquez pour accéder à une zone de dessin


d. En déduire le signe de f(x) sur [1 \: ; 6].
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
72
 [Calculer.]
f est la fonction définie sur \R par f(x) = 3x^4 - 4x^3 + 6x^2 - 12x + 12 .
On note f ^ { \prime } la fonction dérivée de f et on note f ^ { \prime \prime } la fonction dérivée de f ^ { \prime } sur \R.
1. a. Justifier que f puis que f ^ { \prime } sont dérivables sur \R.

b. Déterminer f ^ { \prime \prime } ( x ) puis étudier son signe.

2. Déduire le sens de variation de f ^ { \prime } et dresser son tableau de variations sur \R.


Cliquez pour accéder à une zone de dessin


3. Calculer f ^ { \prime }(1) puis donner le signe de f ^ { \prime }(x) en fonction de x .

4. Dresser le tableau de variations de f .

Cliquez pour accéder à une zone de dessin
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
73
 [Représenter.]
Tracer une courbe \mathcal{C} représentant une fonction f définie et dérivable sur l'intervalle [0 \: ; 5] ayant les propriétés suivantes :
  • f ( 0 ) = 1 \: ;
  • f ( 3 ) = f ( 5 ) = - 1 \: ;
  • f ( 4 ) = \dfrac { - 1 } { 2 } \: ;
  • f est décroissante sur [0 \:; 2] \: ;
  • f ^ { \prime } ( 2 ) = 0, \: f ^ { \prime } (3) = 1 et f ^ { \prime } (5) = -1 \:;
  • f admet en 2 un minimum égal à -3 \: ;
  • pour tout x \in [ 2\: ; 5 ], f(x) \lt 0 \: ;
  • f est croissante sur [2\: ; 4].


Cliquez pour accéder à une zone de dessin

Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
74
 [Calculer.]
1. Soient la fonction f définie sur \R par f ( x ) = 2 x ^ { 2 } - 5 x + 1 et l'inéquation f ( x ) \geqslant 1.
a. Trouver son ensemble de dérivation.

b. Calculer f ^ { \prime } ( x ).


c. Dresser le tableau de variations de f .

Cliquez pour accéder à une zone de dessin


d. Trouver les solutions de l'inéquation proposée.

2. Soient la fonction f définie sur \R par f ( x ) = x ^ { 3 } + 2 x - 1 et l'inéquation f ( x ) \gt - 1.
a. Trouver son ensemble de définition.

b. Calculer f ^ { \prime } ( x ).


c. Dresser le tableau de variations de f .

Cliquez pour accéder à une zone de dessin


d. Trouver les solutions de l'inéquation proposée.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
75
Démo
 [Raisonner.]

f est une fonction définie et dérivable sur \R . On considère l'énoncé suivant :
« Si f admet un extremum local pour x = -1 , alors f ^ { \prime } ( - 1 ) = 0 ».

1. Cet énoncé est-il vrai ? Justifier.

2. Écrire l'énoncé réciproque. Est-il vrai ? Justifier.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
76
 [Raisonner.]
f est une fonction dérivable sur \R et a est un réel. Compléter par « nécessaire » ou « suffisante ».

1. Une condition
pour que f admette un maximum local en un réel a est que f ^ { \prime } ( a ) = 0.
2. Une condition
pour que f ^ { \prime } ( a ) = 0 est que f admette un extremum local en a .
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
77
 [Raisonner.]

f est une fonction définie et dérivable sur un intervalle \text{I.} f ^ { \prime } est la fonction dérivée de f sur \text{I.}
On considère les deux propositions suivantes :
Proposition \text{P :} « \: f(x) = x^2 + 3x \:».
Proposition \text{Q :} « \: f ^ { \prime } ( x ) = 2 x + 3 \:».
Les deux propositions \text{P} et \text{Q} sont-elles équivalentes ? Expliquer.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
78
 [Raisonner.]
g est la fonction définie sur \R par : g(x) = -2x^3 + 3x^2 - 2x + 8 . On note g ^ { \prime } la fonction dérivée de g sur \R . Pour chacune des affirmations ci-dessous, indiquer si elle est vraie ou fausse en justifiant la réponse.
1. g ^ { \prime } ( x ) = - 6 \left( x - \dfrac { 1 } { 2 } \right) ^ { 2 } - \dfrac { 1 } { 2 } \:;

2. g est décroissante sur \R\: ;

3. g(x) est négatif sur \R\: ;

4. g(x) est négatif sur [ 2 \: ; + \infty [\: ;

5. g ( \sqrt { 2 } ) = 14 - 6 \sqrt { 2 }.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
79
 [Raisonner.]

On donne ci-dessous le tableau de variations d'une fonction f définie et dérivable sur \mathcal { D } = [ - 3\: ; 0 [ \cup ] 0\: ; 5 ].

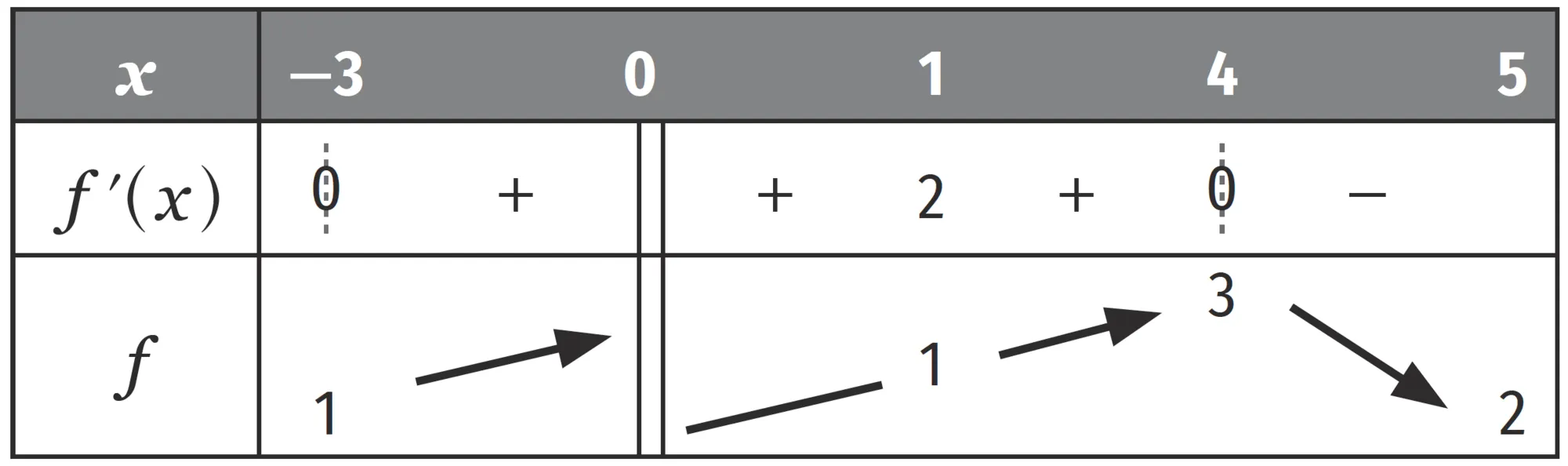
Placeholder pour Tableau variations fonction : valeurs x, f'(x), f. Représentation graphique des variations de f.Tableau variations fonction : valeurs x, f'(x), f. Représentation graphique des variations de f.

Pour chacune des affirmations ci-dessous, indiquer si elle est vraie ou fausse en justifiant la réponse.

1. pour tout x \in ] 0\: ; 5 ] , f(x) \gt 0\: ;

2. f est strictement croissante sur [ - 3\: ; 0 [ \cup ] 0\: ; 1 ]\: ;

3. si f ( x ) \in [ 1\: ; 3 ] alors x \in [ 1 \:; 4 ]\: ;

4. \text{T} est la tangente à la courbe représentative de f au point d'abscisse 1.
Une équation de \text{T} est : 2x - y - 1 = 0 .
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
80
 [Raisonner.]
On donne ci-dessous le tableau de variations d'une fonction f définie et dérivable sur \mathcal { D } = [ - 6\: ; 4 ].

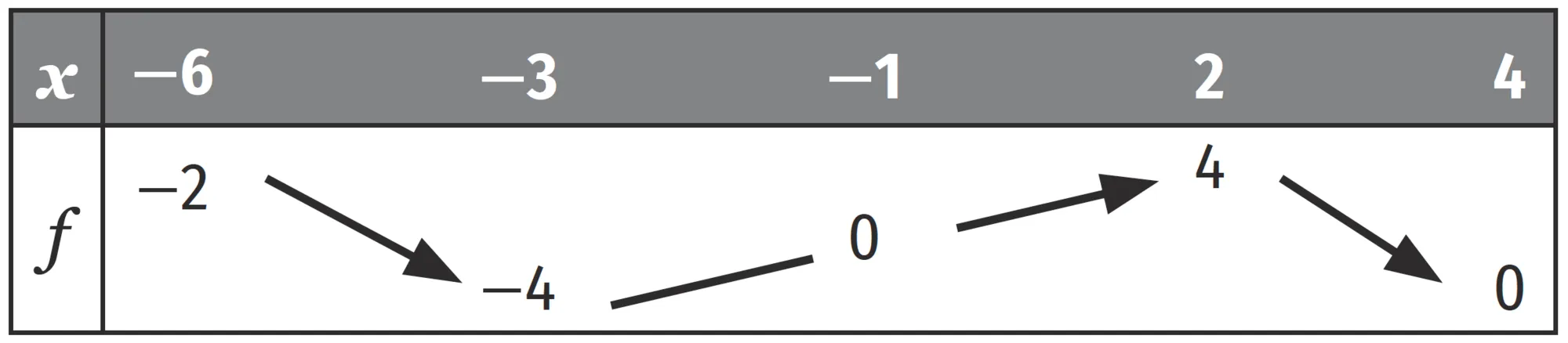
Placeholder pour Diagramme: extrémums d'une fonction mathématique. Valeurs de x et f(x) représentées graphiquement par des flèches.Diagramme: extrémums d'une fonction mathématique. Valeurs de x et f(x) représentées graphiquement par des flèches.

Pour chacune des affirmations ci-dessous, indiquer si elle est vraie ou fausse en justifiant la réponse.

1. le minimum de f sur \mathcal{D} est 0\: ;

2. f ( f ( 2 ) ) = 0\: ;

3. f ^ { \prime } ( - 3 ) = 0\: ;

4. ( f ( - 5 ) ) ^ { 2 } \gt ( f ( 5 ) ) ^ { 2 } \:;

5. f ^ { \prime } ( 3 ) \gt 0.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
81
QCM
[Raisonner.]
f et g sont les fonctions définies sur \R par f ( x ) = \dfrac { - 2 x } { x ^ { 2 } + 1 } et g ( x ) = \dfrac { ( x - 1 ) ^ { 2 } } { x ^ { 2 } + 1 }.
Parmi les réponses proposées, choisir celles qui sont correctes en justifiant.
1. pour tout x \in \mathbb { R }, f(x) = g(x)\: ;

2. pour tout x \in \mathbb { R }, f ^ { \prime } ( x ) = g ^ { \prime } ( x )\: ;

3. f est strictement décroissante sur [-1 \: ; 1] \: ;

4. pour tout x \in \mathbb { R }, f ( x ) \leqslant 2.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
82
QCM
[Raisonner.]

g est la fonction définie sur \R par g(x) = x^4 - 4x^3 .
Parmi les réponses proposées, choisir celles qui sont correctes en justifiant.

1. g est croissante sur [ 3 \:; + \infty [ \: ;

2. g est positive sur [ 3 \:; 4 ] \: ;

3. g admet un extremum en 0\: ;

4. g admet un extremum en 3\: ;

5. g ^ { \prime } est négative sur [2 \: ; 3] \:;

6. g ^ { \prime } est décroissante sur [0 \: ; 2].
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
83
QCM
[Raisonner.]
h est la fonction définie sur ] 0 \: ; + \infty [ par h ( x ) = x + \dfrac { 1 } { x }.
Parmi les réponses proposées, choisir celles qui sont correctes en justifiant.

1. h est croissante sur ] 0 \: ; + \infty [ \: ;

2. h est croissante sur ] 1 \: ; + \infty [ \: ;

3. 10\text{,}1 est le maximum de h sur ]0 \:; 10]\: ;

4. 2 est le minimum de h sur ] 0 \: ; + \infty [ \: ;

5. 1 est le minimum de h sur ] 0 \: ; + \infty [ \: ;

6. h n'admet pas de maximum sur ] 0 \: ; + \infty [.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
84
Python
 [Calculer.]
Dans une usine, le coût de fabrication unitaire d'un article est donné par la fonction f définie sur [0\text{,}5\: ; 3] par f ( x ) = \dfrac { x ^ { 2 } - 2 x + 2 } { x } où x est le nombre de milliers d'articles fabriqués.
f(x) est exprimé en millier d'euros.
1. Quel est le coût unitaire de fabrication de 500 articles ? 501 articles ?

2. Démontrer que la fonction f admet un minimum sur [0\text{,}5\: ; 3].

3. Compléter le programme ci-dessous afin qu'il retrouve la valeur de x pour laquelle le coût unitaire est minimal. 

def Fabrication(f1, f2, x):
while f1 > f2: 
	x = x + 0.001
  f1 = f2
  f2 = ...
return ...

print(Fabrication(2.5, 2.493, 0.501))
Cliquez pour accéder à la correction


Afficher la correction
Page suivante
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.