Mathématiques 1re Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 5
Applications de la dérivation
Ressource affich ée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Capacités attendues
1. Faire le lien entre signe de la dérivée et sens de variation d'une fonction.
2. Déterminer les extremums d'une fonction à partir de sa dérivée.
3. Résoudre un problème d'optimisation.
4. Exploiter les variations d'une fonction pour établir une inégalité.
2. Déterminer les extremums d'une fonction à partir de sa dérivée.
3. Résoudre un problème d'optimisation.
4. Exploiter les variations d'une fonction pour établir une inégalité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le barrage de Vouglans dans le Jura est la troisième plus grande retenue artificielle d'eau de France. La forme de sa voûte est calculée pour minimiser les forces de pression de l'eau qui s'exercent sur la paroi. Le calcul de fonctions dérivées est nécessaire pour obtenir cette forme.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Avant de commencer
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Prérequis
1. Déterminer le sens de variation d'une fonction.
2. Déterminer les extremums d'une fonction.
3. Dresser, à partir d'une lecture graphique, le tableau de variations d'une fonction.
4. Calculer des fonctions dérivées.
2. Déterminer les extremums d'une fonction.
3. Dresser, à partir d'une lecture graphique, le tableau de variations d'une fonction.
4. Calculer des fonctions dérivées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
En 2015, un manuscrit ayant appartenu à Alan Turing s'est vendu aux enchères pour un million de dollars.
Dans ce manuscrit, Turing avait par exemple écrit qu'il trouvait la notation de Gottfried W. Leibniz \dfrac { \text{d} x } { \text{d} y } extrêmement difficile à comprendre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Utiliser un tableau de variations
On donne ci-dessous le tableau de variations d'une fonction k .
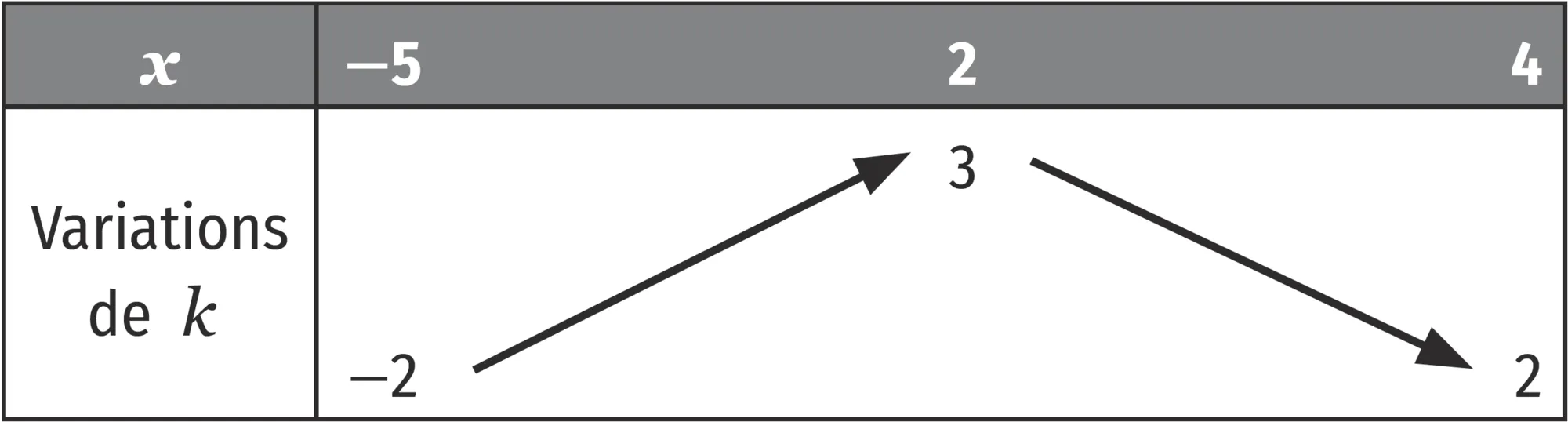
a. k(-4) et k(0) \: ?
b. k(3) et k(3\text{,}9) \: ?
c. k(1) et k(3) \: ?
d. k(-5) et k(3) \: ?
2. Déterminer les extremums de k sur l'intervalle [-5\: ; 4].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Utiliser une lecture graphique
On donne ci-dessous la courbe \mathcal{C}_g représentative d'une fonction g .
\text{T}_{-2} , \text{T}_{1} et \text{T}_{4} sont les tangentes à \mathcal{C}_g aux points d'abscisses respectifs -2\: ; 1 et 4 . 1. Donner, par lecture graphique :
a. les valeurs de g(4) et g ^ { \prime } (4) \: ;
b. les valeurs de g(1) et g ^ { \prime } ( 1 ) \: ;
c. le signe de g ^ { \prime } ( - 2 ) et le sens de variation de g sur [-3\: ; - 1] \: ;
d. le minimum de g sur [-2\: ; 7].
2. Soit x \in [ - 1 \:; 9 ]. Donner un encadrement de g(x).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Calculer des fonctions dérivées
Calculer la dérivée des fonctions définies par :
1. f ( x ) = x ^ { 3 } - 6 x - 4 , sur \mathbb { R }\: ;
2. g ( x ) = - x ( 2 x - 3 ), sur \mathbb { R }\: ;
2. g ( x ) = - x ( 2 x - 3 ), sur \mathbb { R }\: ;
3. h ( x ) = \dfrac { x ^ { 2 } + 3 } { x + 1 }, sur ]-1\: ; + \infty[ \: ;
4. k ( x ) = \dfrac { 2 } { x } + \sqrt { x } + 2 x sur ]0\: ; + \infty[ .
4. k ( x ) = \dfrac { 2 } { x } + \sqrt { x } + 2 x sur ]0\: ; + \infty[ .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Problème
Une ligne électrique rectiligne doit relier les deux
stations \text{A} et \text{B} tout en passant par la ville \text{M.}
On souhaite construire les deux stations \text{A} et \text{B} afin que la longueur de la ligne électrique soit minimale.
On suppose que le plan est assimilé à un repère orthonormal et que la ville \text{M} correspond au point de coordonnées (10\: ; 10).
1. On suppose que l'abscisse de \text{A} est a , avec a \gt 10 . Montrer que l'ordonnée de \text{B} est \dfrac { 10 a } { a - 10 }.
On souhaite construire les deux stations \text{A} et \text{B} afin que la longueur de la ligne électrique soit minimale.
On suppose que le plan est assimilé à un repère orthonormal et que la ville \text{M} correspond au point de coordonnées (10\: ; 10).
2. Justifier que \mathrm { AB } ^ { 2 } = a ^ { 2 } + \dfrac { 100 a ^ { 2 } } { ( a - 10 ) ^ { 2 } }.
3. a. Tracer à la calculatrice la courbe représentative de la fonction f définie sur ]10\: ; + \infty[ par f ( x ) = x ^ { 2 } + \dfrac { 100 x ^ { 2 } } { ( x - 10 ) ^ { 2 } } puis déterminer graphiquement son minimum.
b. En déduire les coordonnées des points \text{A} et \text{B.}
3. a. Tracer à la calculatrice la courbe représentative de la fonction f définie sur ]10\: ; + \infty[ par f ( x ) = x ^ { 2 } + \dfrac { 100 x ^ { 2 } } { ( x - 10 ) ^ { 2 } } puis déterminer graphiquement son minimum.
b. En déduire les coordonnées des points \text{A} et \text{B.}
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
