Chapitre 5
Cours 1
Dérivée et sens de variation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ADu signe de la dérivée au sens de variation d'une fonction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Théorème
Soient f une fonction dérivable sur un intervalle \text{I} et f ^ { \prime } la fonction dérivée de f .
- Si f ^ { \prime } est strictement positive sur \text{I,} sauf pour un nombre fini de réels où elle s'annule, alors f est strictement croissante sur \text{I.}
- Si f ^ { \prime } est strictement négative sur \text{I,} sauf pour un nombre fini de réels où elle s'annule, alors f est strictement décroissante sur \text{I.}
- Si f ^ { \prime }est nulle sur \text{I,} alors f est constante sur \text{I.}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Avec ce théorème, on peut démontrer que les fonctions f et -f sont de variations contraires sur un intervalle \text{I} où elles sont dérivables.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour les deux premiers points, f ^ { \prime } ne doit pas s'annuler sur un intervalle \text {J} \subset \mathrm {I} pour que le théorème
soit valide.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
Démontrons le premier point. On admet le résultat suivant : « pour tous réels a
et b de \text{I,} il existe un réel c \in ] a\: ; b [ tel que f ^ { \prime } ( c ) = \dfrac { f ( b ) - f ( a ) } { b - a } ».
Soient a et b deux réels de \text{I} tels que a \lt b ( donc b - a \gt 0 ).
Il existe c \in \text{I} tel que f ^ { \prime } ( c ) = \dfrac { f ( b ) - f ( a ) } { b - a }.
Puisque f ^ { \prime } est positive alors f ^ { \prime } ( c ) = \dfrac { f ( b ) - f ( a ) } { b - a } \gt 0, donc f ( b ) - f ( a ) \gt 0 et ainsi f ( a ) \lt f ( b ) : la fonction f est bien strictement croissante.
On raisonne de façon analogue pour les deux autres points.
Soient a et b deux réels de \text{I} tels que a \lt b ( donc b - a \gt 0 ).
Il existe c \in \text{I} tel que f ^ { \prime } ( c ) = \dfrac { f ( b ) - f ( a ) } { b - a }.
Puisque f ^ { \prime } est positive alors f ^ { \prime } ( c ) = \dfrac { f ( b ) - f ( a ) } { b - a } \gt 0, donc f ( b ) - f ( a ) \gt 0 et ainsi f ( a ) \lt f ( b ) : la fonction f est bien strictement croissante.
On raisonne de façon analogue pour les deux autres points.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le résultat admis est le théorème des accroissements finis, non étudié en première.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
f est la fonction définie sur \R par f(x) = x^3.
f est dérivable sur \R et f ^ { \prime } ( x ) = 3 x ^ { 2 }.
f ^ { \prime } s'annule uniquement en 0 et est strictement positive pour tout x \neq 0, donc f est strictement croissante sur \R.
f est dérivable sur \R et f ^ { \prime } ( x ) = 3 x ^ { 2 }.
f ^ { \prime } s'annule uniquement en 0 et est strictement positive pour tout x \neq 0, donc f est strictement croissante sur \R.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Étudier le sens de variation de la fonction f : x \mapsto - x ^ { 3 } - 2 x + 5, puis dresser son tableau de variations.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
f est une fonction polynôme du troisième degré, donc f est définie et
dérivable sur \R.
f ^ { \prime } ( x ) = - 3 x ^ { 2 } - 2.
Pour tout x \in \mathbb { R } , - 3 x ^ { 2 } \leqslant 0 et - 2 \lt 0, donc f ^ { \prime } ( x ) \lt 0 et ainsi f est strictement décroissante sur \R.

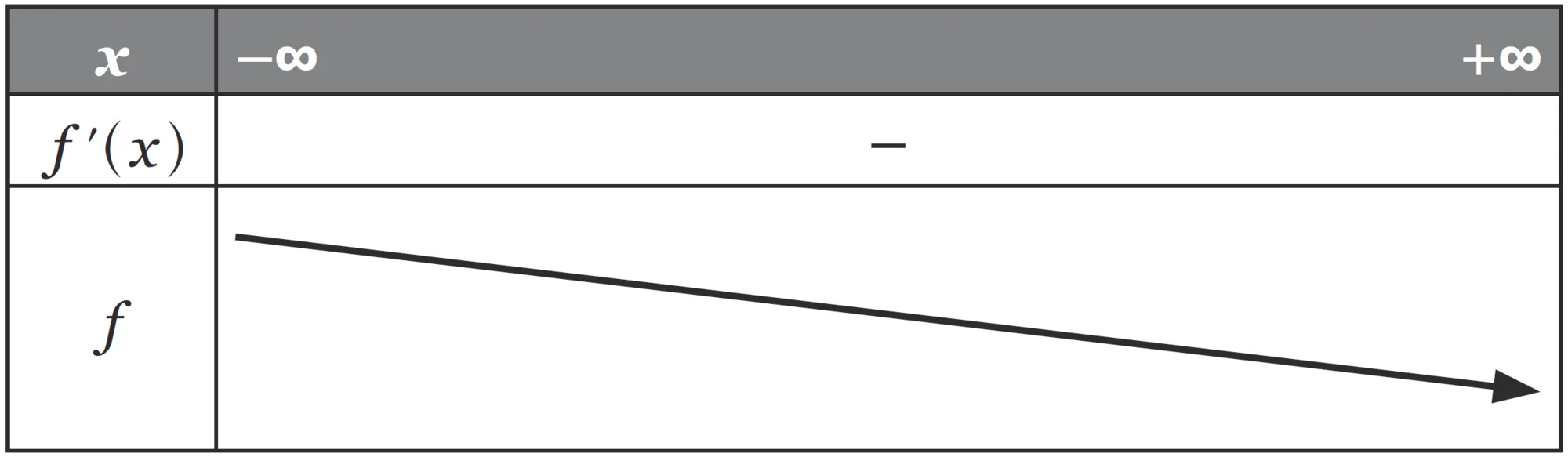
f ^ { \prime } ( x ) = - 3 x ^ { 2 } - 2.
Pour tout x \in \mathbb { R } , - 3 x ^ { 2 } \leqslant 0 et - 2 \lt 0, donc f ^ { \prime } ( x ) \lt 0 et ainsi f est strictement décroissante sur \R.


Pour s'entraîner
exercices ; et p. 143
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour étudier les variations d'une fonction sur son ensemble de définition :
1. on justifie qu'elle est dérivable ;
2. on détermine sa dérivée ;
3. on étudie le signe de la dérivée ;
4. on en déduit le sens de variation de la fonction.
1. on justifie qu'elle est dérivable ;
2. on détermine sa dérivée ;
3. on étudie le signe de la dérivée ;
4. on en déduit le sens de variation de la fonction.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BDu sens de variation au signe de la dérivée
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Théorème
Soient f une fonction dérivable sur un intervalle \text{I} et f ^ { \prime } la fonction dérivée de f .
- Si f est croissante sur \text{I,} alors f ^ { \prime } est positive sur \text{I.}
- Si f est décroissante sur \text{I,} alors f ^ { \prime } est négative sur \text{I.}
- Si f est constante sur \text{I,} alors f ^ { \prime } est nulle sur \text{I.}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ce théorème et le précédent peuvent être regroupés en un seul théorème écrit sous forme d'une équivalence.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
Soit h > 0 tel que x + h \in \mathrm { I }.
Pour tout x \in \mathrm { I } , f ^ { \prime } ( x ) =\mathop{\lim}\limits_{h \rightarrow 0} \dfrac { f ( x + h ) - f ( x ) } { h }.
On remarque que, pour tout x \in \mathrm { I}, x + h \gt x.
Pour tout x \in \mathrm { I } , f ^ { \prime } ( x ) =\mathop{\lim}\limits_{h \rightarrow 0} \dfrac { f ( x + h ) - f ( x ) } { h }.
On remarque que, pour tout x \in \mathrm { I}, x + h \gt x.
Si f est croissante sur \text{I} alors, pour tout x \in \mathrm {I} , f ( x + h ) \geqslant f ( x ) donc f ( x + h ) - f ( x ) \geqslant 0 donc f ^ { \prime } ( x ) \geqslant 0.
Si f est décroissante sur \text{I} alors, pour tout x \in \mathrm {I} , f ( x + h ) \leqslant f ( x ) donc f ( x + h ) - f ( x ) \leqslant 0 donc f ^ { \prime } ( x ) \leqslant 0.
Si f est constante sur \text{I} alors, pour tout x \in \mathrm {I} , f ( x + h ) = f( x ) donc f ( x + h ) - f ( x ) = 0 donc f ^ { \prime } ( x ) = 0.
Si f est décroissante sur \text{I} alors, pour tout x \in \mathrm {I} , f ( x + h ) \leqslant f ( x ) donc f ( x + h ) - f ( x ) \leqslant 0 donc f ^ { \prime } ( x ) \leqslant 0.
Si f est constante sur \text{I} alors, pour tout x \in \mathrm {I} , f ( x + h ) = f( x ) donc f ( x + h ) - f ( x ) = 0 donc f ^ { \prime } ( x ) = 0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
C _ { f } et C _ { g } représentent respectivement une fonction f et g , chacune définie et dérivable sur l'intervalle \text{I} = [ 1 \: ; 5 ].
Toutes les tangentes à C _ { f } sur \text{I} ont un coefficient directeur positif car f est croissante : on en déduit que f ^ { \prime } est positive sur \text{I.}
Celles à C _ { g } ont un coefficient directeur négatif car g est décroissante : on en déduit que g ^ { \prime } est négative sur \text{I.}
Toutes les tangentes à C _ { f } sur \text{I} ont un coefficient directeur positif car f est croissante : on en déduit que f ^ { \prime } est positive sur \text{I.}
Celles à C _ { g } ont un coefficient directeur négatif car g est décroissante : on en déduit que g ^ { \prime } est négative sur \text{I.}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
\mathcal{C}_g est la courbe représentative d'une fonction g définie et dérivable sur [-3 \: ; 4].
Donner graphiquement, suivant les valeurs de x , le signe de g ^ { \prime } ( x ).

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour déterminer le signe de la dérivée à partir du sens de variation :
1. on détermine les intervalles sur lesquels la fonction est croissante et les intervalles sur lesquels elle est décroissante ;
2. Si la fonction est croissante (respectivement décroissante) alors la dérivée est positive (respectivement négative).
1. on détermine les intervalles sur lesquels la fonction est croissante et les intervalles sur lesquels elle est décroissante ;
2. Si la fonction est croissante (respectivement décroissante) alors la dérivée est positive (respectivement négative).
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

