Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 5
TP / TICE 2
Résolution d'une équation du troisième degré
11 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions préliminaires
1. Démontrer que \mathcal { P } et \mathcal { H } ont un seul point d'intersection si et seulement si l'équation \text { (E) } x ^ { 3 } + 4 x - 8 = 0 admet une unique solution.
2. f est la fonction définie sur \R par f(x) = x^3 + 4x - 8 . Étudier les variations de f sur \R puis dresser son tableau de variations. Conjecturer le nombre de solutions à l'équation f(x) = 0 sur [1\: ; 2].
2. f est la fonction définie sur \R par f(x) = x^3 + 4x - 8 . Étudier les variations de f sur \R puis dresser son tableau de variations. Conjecturer le nombre de solutions à l'équation f(x) = 0 sur [1\: ; 2].
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Utiliser des algorithmes déjà vus en seconde pour
déterminer une valeur approchée de la solution de
l'équation \text{(E)} à l'aide d'une des trois méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Calculatrice
Par balayage : on note a la solution de \text{(E)}.
1. Tracer, à la calculatrice, la courbe représentative
de la fonction f.
2. Par lecture graphique, retrouver un encadrement à l'unité de la solution a. Justifier.
2. Par lecture graphique, retrouver un encadrement à l'unité de la solution a. Justifier.
3. À l'aide du tableau de valeurs de la calculatrice,
donner un encadrement de a d'amplitude 10^{-1} puis un encadrement d'amplitude 10^{-2}.
4. Poursuivre le même procédé, donner un encadrement de a d'amplitude 10^{-3}.
4. Poursuivre le même procédé, donner un encadrement de a d'amplitude 10^{-3}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Tableur
Par balayage : on note a la solution de (\text{E}).
1. On commence par chercher un encadrement
de a d'amplitude 10^{-1}.
a. Reproduire la feuille de calcul ci-dessous.
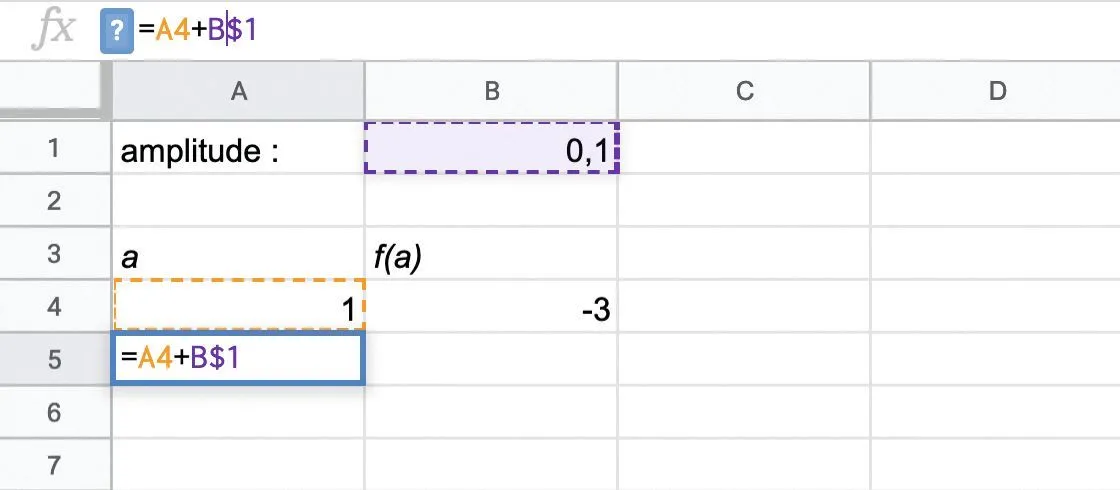
b. Quelle formule faut-il entrer dans la cellule B4 ?
c. Justifier la formule entrée dans la cellule A5, notamment l'utilisation du symbole $.
a. Reproduire la feuille de calcul ci-dessous.
Le zoom est accessible dans la version Premium.
b. Quelle formule faut-il entrer dans la cellule B4 ?
c. Justifier la formule entrée dans la cellule A5, notamment l'utilisation du symbole $.
d. Compléter la feuille de calcul pour obtenir toutes
les valeurs de a avec un pas de 0\text{,}1.
e. En se rappelant que f(a) = 0, en déduire un encadrement de a d'amplitude 10^{-1}.
2. Modifier la feuille de calcul pour obtenir un encadrement de a d'amplitude 10^{-2}.
3. Faire une nouvelle modification pour obtenir cette fois un encadrement de a d'amplitude 10^{-3}.
e. En se rappelant que f(a) = 0, en déduire un encadrement de a d'amplitude 10^{-1}.
2. Modifier la feuille de calcul pour obtenir un encadrement de a d'amplitude 10^{-2}.
3. Faire une nouvelle modification pour obtenir cette fois un encadrement de a d'amplitude 10^{-3}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 3Python
Dans cette partie, on cherche à trouver, avec la méthode de dichotomie, un encadrement de la
solution notée a de l'équation \text{(E).} On note respectivement u et v les bornes d'un intervalle dans lequel se trouve a. Au début de l'algorithme, on admet alors que u = 1 et v = 2 .
1. Sans faire de calcul, justifier, à l'aide de la question préliminaire 2. , que f(u) \times f(v) \lt 0 .
2. On pose m = \dfrac { u + v } { 2 }.
a. Que représente m pour u et v \: ? Pour l'intervalle [u \: ; v] \: ?
b. Justifier que, si \alpha \in ] u \: ; m [, alors f(u) \times f(m) \lt 0 .
c. Quel est le signe de f(u) \times f(m) lorsque \alpha \in ] m \: ; v [ \: ? Justifier.
2. On pose m = \dfrac { u + v } { 2 }.
a. Que représente m pour u et v \: ? Pour l'intervalle [u \: ; v] \: ?
b. Justifier que, si \alpha \in ] u \: ; m [, alors f(u) \times f(m) \lt 0 .
c. Quel est le signe de f(u) \times f(m) lorsque \alpha \in ] m \: ; v [ \: ? Justifier.
3. Recopier et compléter l'algorithme ci-dessous afin qu'il donne un encadrement de a d'amplitude 10^{-1}.
4. Expliquer le fonctionnement de cet algorithme.
5. Sur Python, programmer l'algorithme ci-dessus et donner un encadrement de a d'amplitude 10^{-2} puis d'amplitude 10^{-3}.
\boxed{
\begin{array} { l } { u \leftarrow 1 } \\
v \leftarrow 2 \\
\text{Tant que } v - u > \text { ... } \\
\quad \text {Si } f ( u ) \times f ( ( u + v ) / 2 ) \lt 0 : \\
\quad \quad v \leftarrow ( u + v ) / 2 \\
\quad \text {Sinon :} \\
\quad \quad u \leftarrow \text { ... } \\
\quad \text {Fin Si}\\
\text {Fin Tant que}\\
\end{array}
}
4. Expliquer le fonctionnement de cet algorithme.
5. Sur Python, programmer l'algorithme ci-dessus et donner un encadrement de a d'amplitude 10^{-2} puis d'amplitude 10^{-3}.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah