Chapitre 6
Cours 2
Étude de la fonction exponentielle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ASigne de la fonction exponentielle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Pour tout nombre réel x, \mathrm{e}^{x} > 0 .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
\mathrm{e}^{3}>0 et \mathrm{e^{-5}}>0
L'équation \mathrm{e}^{x} = -4 n'admet pas de solution car -4 est négatif alors que pour tout x, \mathrm{e}^{x} > 0 . Autrement dit, -4 n'admet pas d'antécédent par la fonction exponentielle.
L'équation \mathrm{e}^{x} = -4 n'admet pas de solution car -4 est négatif alors que pour tout x, \mathrm{e}^{x} > 0 . Autrement dit, -4 n'admet pas d'antécédent par la fonction exponentielle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
Pour tout nombre réel x, on a \mathrm{e}^{x}=\mathrm{e}^{\normalsize{\frac{x}{2}+\frac{x}{2}}}=\mathrm{e}^{\normalsize{\frac{x}{2}}} \times \mathrm{e}^{\normalsize{\frac{x}{2}}}=\left(\mathrm{e}^{\normalsize{\frac{x}{2}}}\right)^{2}.
Dans \mathbb{R} , un carré est
toujours positif ou nul. Or, la fonction exponentielle ne s'annule jamais sur \mathbb{R} , donc, pour tout nombre réel x, \left(\mathrm{e}^{\frac{x}{2}}\right)^{2}>0 d'où \mathrm{e}^{x}>0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Donner le signe des expressions suivantes :
\mathrm{e}^{-x} et \mathrm{-e}^{-3 x-1}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On utilise le fait que la fonction exponentielle est
strictement positive sur \mathbb{R}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BVariations de la fonction exponentielle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
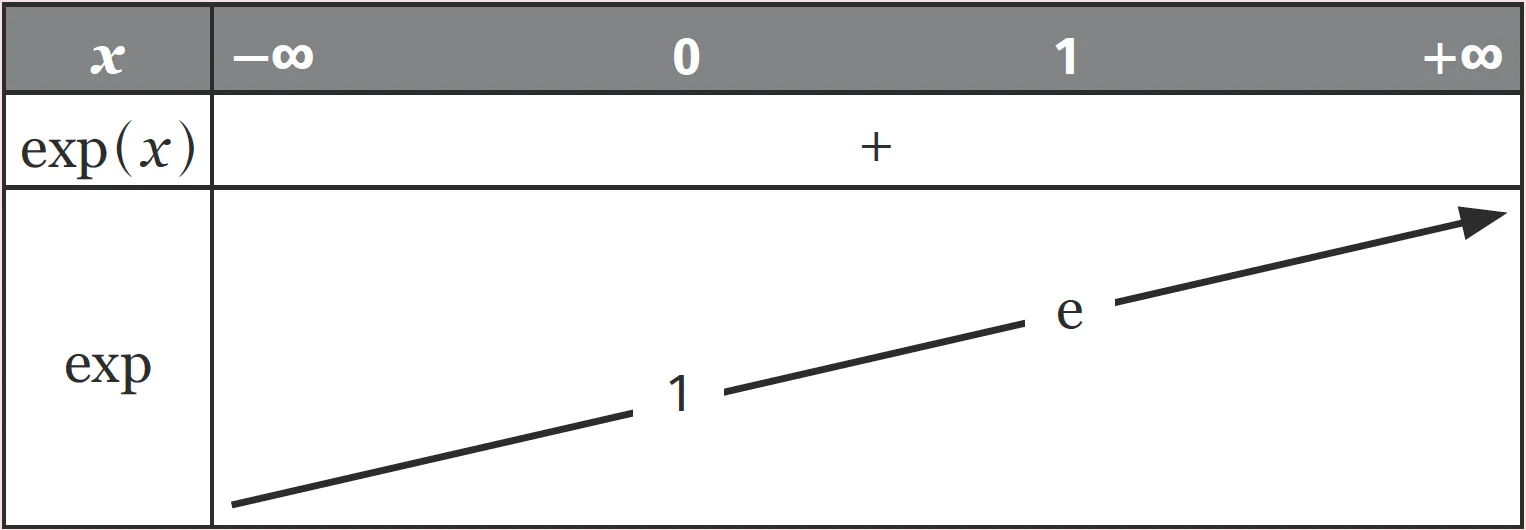
La fonction exponentielle est strictement croissante sur \mathbb{R} .





Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
Pour tout nombre réel x , \exp ^{\prime}(x)=\exp (x)>0.
La fonction dérivée de la fonction exponentielle est strictement positive sur \mathbb{R} donc la fonction exponentielle est strictement croissante sur \mathbb{R}.
La fonction dérivée de la fonction exponentielle est strictement positive sur \mathbb{R} donc la fonction exponentielle est strictement croissante sur \mathbb{R}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Pour tous réels a et b fixés, la fonction f définie sur \mathbb{R} par f(x) = \mathrm{e}^{ax+b} est
dérivable sur \mathbb{R} et, pour tout réel x , f^{\prime}(x)=a \mathrm{e}^{a x+b}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On
calcule ici la dérivée
de la composée de la
fonction exponentielle
avec une
fonction affine.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
On applique directement la formule pour obtenir le
résultat souhaité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
La fonction h définie sur \mathbb{R} par h(x)=-3 \, e^{2 x-5}+1 est dérivable sur \mathbb{R} et, pour
tout réel x, h^{\prime}(x)=2 \times\left(-3\, \mathrm{e}^{2 x-5}\right)=-6 \, \mathrm{e}^{2 x-5}. Pour tout réel x , \mathrm{e}^{2 x-5}>0 , donc on en
déduit que h^{\prime}(x) \lt 0. Par conséquent, h est strictement décroissante sur \mathbb{R}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Étudier les variations des fonctions f et g définies sur \mathbb{R} par :
1. f(x)=\mathrm{e}^{x}+x
2. g(x)=\mathrm{e}^{-2 x+6}
2. g(x)=\mathrm{e}^{-2 x+6}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. On calcule la fonction dérivée de f
puis on étudie le signe de f'(x).
2. x \mapsto f(a x+b) a pour fonction dérivée x \mapsto a \times f^{\prime}(a x+b).
2. x \mapsto f(a x+b) a pour fonction dérivée x \mapsto a \times f^{\prime}(a x+b).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
1. f est dérivable sur \mathbb{R} et, pour tout réel x , f^{\prime}(x)=\mathrm{e}^{x}+1.
Or, \mathrm{e}^{x}+1 \geqslant 0 \Leftrightarrow \mathrm{e}^{x} \geqslant-1, ce qui est vrai pour tout nombre réel x .
L'équation f^{\prime}(x)=0 n'admet pas de solution. Donc f^{\prime}(x)>0 sur \mathbb{R} et f
est strictement croissante sur \mathbb{R}.
2. g est dérivable sur \mathbb{R} et, pour tout réel x, g^{\prime}(x)=-2 \times \mathrm{e}^{-2 x+6}. Or, pour tout réel x, \mathrm{e}^{-2 x+6}>0 donc g^{\prime}(x)\lt 0 sur \mathbb{R}. Par conséquent, g est strictement décroissante sur \mathbb{R}.
2. g est dérivable sur \mathbb{R} et, pour tout réel x, g^{\prime}(x)=-2 \times \mathrm{e}^{-2 x+6}. Or, pour tout réel x, \mathrm{e}^{-2 x+6}>0 donc g^{\prime}(x)\lt 0 sur \mathbb{R}. Par conséquent, g est strictement décroissante sur \mathbb{R}.
Pour s'entraîner
Exercices et p. 171
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CRésolution d'équations et d'inéquations
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Pour tous nombres réels a et b :
\mathrm{e}^{a}=\mathrm{e}^{b} \Leftrightarrow a=b
\mathrm{e}^{a} \lt \mathrm{e}^{b} \Leftrightarrow a \lt b
\mathrm{e}^{a}>\mathrm{e}^{b} \Leftrightarrow a>b
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Il est
bon de connaître
par cœur :
\mathrm{e}^{x} \geqslant 1 \Leftrightarrow x \geqslant 0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
La fonction exponentielle est strictement croissante sur \mathbb{R} donc :
deux images égales ont nécessairement le même antécédent ;
deux nombres et leur image sont classés dans le même ordre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
\mathrm{e}^{x}=\mathrm{e}^{7} \Leftrightarrow x=7 et \mathrm{e}^{x} \lt \mathrm{e}^{-2} \Leftrightarrow x \lt -2
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ÉnoncéRésoudre des équations et des inéquations
Résoudre dans \mathbb{R} l'équation \mathrm{e}^{2 x}=\dfrac{1}{\mathrm{e}} puis
\mathrm{e}^{-3 x+4}+1 \geqslant 2.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On utilise les propriétés algébriques de la fonction
exponentielle pour se ramener à des équations du
type \mathrm{e}^{a}=\mathrm{e}^{b} ou \mathrm{e}^{a} \leqslant \mathrm{e}^{b}.
On se sert ensuite des propriétés \mathrm{e}^a = \mathrm{e}^{b} \Leftrightarrow a = b et \mathrm{e}^a \leqslant \mathrm{e}^b \Leftrightarrow a \leqslant b .
On se sert ensuite des propriétés \mathrm{e}^a = \mathrm{e}^{b} \Leftrightarrow a = b et \mathrm{e}^a \leqslant \mathrm{e}^b \Leftrightarrow a \leqslant b .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
\Leftrightarrow \mathrm{e}^{2 x}=\mathrm{e}^{-1}
\Leftrightarrow 2 x=-1
\Leftrightarrow x=-\dfrac{1}{2}
L'équation \mathrm{e}^{2 x}=\dfrac{1}{\mathrm{e}} a pour unique solution -\dfrac{1}{2}.
\Leftrightarrow \mathrm{e}^{-3 x+4} \geqslant 1
\Leftrightarrow \mathrm{e}^{-3 x+4} \geqslant \mathrm{e}^{0}
\Leftrightarrow-3 x+4 \geqslant 0
\Leftrightarrow x \leqslant \dfrac{4}{3}
L'ensemble des solutions de l'inéquation \mathrm{e}^{-3 x+4}+1 \geqslant 2 est l'intervalle ]-\infty\, ; \dfrac{4}{3} ].
Pour s'entraîner
Exercices à
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ÉnoncéUtiliser les variations de la fonction exponentielle
On considère la fonction f définie et dérivable sur [-2\, ; 2] par f(x)=\dfrac{-b}{8}\left(\exp \left(\dfrac{x}{b}\right)+\exp \left(\dfrac{-x}{b}\right)\right) où b est un réel fixé strictement positif.
Déterminer les variations de la fonction f sur son ensemble de définition.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Pour étudier cette fonction, on utilise les
propriétés de la fonction exponentielle :
La fonction dérivée de x \mapsto \exp (a x+b) est x \mapsto a \exp (a x+b).
\begin{aligned} \exp (a)-\exp (b)=0 & \Leftrightarrow \exp (a)=\exp (b) \\ & \Leftrightarrow a=b \end{aligned}
car la fonction exponentielle est strictement monotone sur \mathbb{R} .
\begin{aligned} \exp (a)-\exp (b)>0 & \Leftrightarrow \exp (a)>\exp (b) \\ & \Leftrightarrow a>b \end{aligned}
car la fonction exponentielle est strictement croissante sur \mathbb{R} .
2. Il faut également penser à simplifier au
maximum l'expression de la dérivée pour
permettre l'utilisation des propriétés de la
fonction exponentielle.
3. Le lien entre les variations d'une fonction et le signe de sa dérivée doit évidemment être connu et utilisé.
car la fonction exponentielle est strictement croissante sur \mathbb{R} .
3. Le lien entre les variations d'une fonction et le signe de sa dérivée doit évidemment être connu et utilisé.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
D'après l'énoncé, la fonction f est dérivable sur [-2\, ; 2].
La dérivée de x \mapsto \dfrac{x}{b} est \dfrac{1}{b}, donc la dérivée de x \mapsto \exp \left(\dfrac{x}{b}\right) est \dfrac{1}{b} \times \exp \left(\dfrac{x}{b}\right).
La dérivée de x \mapsto \dfrac{-x}{b} est \dfrac{-1}{b}, donc la dérivée de x \mapsto \exp \left(\dfrac{-x}{b}\right) est \dfrac{-1}{b} \times \exp \left(\dfrac{-x}{b}\right).
Ainsi, pour tout x \in[-2\, ; 2], f^{\prime}(x)=\dfrac{-b}{8}\left(\dfrac{1}{b} \times \exp \left(\dfrac{x}{b}\right)-\dfrac{1}{b} \times \exp \left(\dfrac{-x}{b}\right)\right).
En simplifiant par b , on obtient f^{\prime}(x)=\dfrac{-1}{8}\left(\exp \left(\dfrac{x}{b}\right)-\exp \left(\dfrac{-x}{b}\right)\right).
Puisque \dfrac{-1}{8} \lt 0, le signe de f' est du signe contraire de \exp \left(\dfrac{x}{b}\right)-\exp \left(\dfrac{-x}{b}\right).
D'une part, \exp \left(\dfrac{x}{b}\right)-\exp \left(\dfrac{-x}{b}\right)=0
\Leftrightarrow \exp \left(\dfrac{x}{b}\right)=\exp \left(\dfrac{-x}{b}\right)
\Leftrightarrow \dfrac{x}{b}=\dfrac{-x}{b} \Leftrightarrow x=0.
D'autre part, \exp \left(\dfrac{x}{b}\right)-\exp \left(\dfrac{-x}{b}\right)>0
\Leftrightarrow \exp \left(\dfrac{x}{b}\right)>\exp \left(\dfrac{-x}{b}\right)
\Leftrightarrow \dfrac{x}{b}>\dfrac{-x}{b}
\Leftrightarrow x>0.
On en déduit alors que f^{\prime}(x)=0 \Leftrightarrow x=0 \text { et } f^{\prime}(x)>0 \Leftrightarrow x \lt 0.
La fonction f est donc croissante sur [-2 ; 0] et décroissante sur [0 ;2].
La dérivée de x \mapsto \dfrac{x}{b} est \dfrac{1}{b}, donc la dérivée de x \mapsto \exp \left(\dfrac{x}{b}\right) est \dfrac{1}{b} \times \exp \left(\dfrac{x}{b}\right).
La dérivée de x \mapsto \dfrac{-x}{b} est \dfrac{-1}{b}, donc la dérivée de x \mapsto \exp \left(\dfrac{-x}{b}\right) est \dfrac{-1}{b} \times \exp \left(\dfrac{-x}{b}\right).
Ainsi, pour tout x \in[-2\, ; 2], f^{\prime}(x)=\dfrac{-b}{8}\left(\dfrac{1}{b} \times \exp \left(\dfrac{x}{b}\right)-\dfrac{1}{b} \times \exp \left(\dfrac{-x}{b}\right)\right).
En simplifiant par b , on obtient f^{\prime}(x)=\dfrac{-1}{8}\left(\exp \left(\dfrac{x}{b}\right)-\exp \left(\dfrac{-x}{b}\right)\right).
Puisque \dfrac{-1}{8} \lt 0, le signe de f' est du signe contraire de \exp \left(\dfrac{x}{b}\right)-\exp \left(\dfrac{-x}{b}\right).
D'une part, \exp \left(\dfrac{x}{b}\right)-\exp \left(\dfrac{-x}{b}\right)=0
\Leftrightarrow \exp \left(\dfrac{x}{b}\right)=\exp \left(\dfrac{-x}{b}\right)
\Leftrightarrow \dfrac{x}{b}=\dfrac{-x}{b} \Leftrightarrow x=0.
D'autre part, \exp \left(\dfrac{x}{b}\right)-\exp \left(\dfrac{-x}{b}\right)>0
\Leftrightarrow \exp \left(\dfrac{x}{b}\right)>\exp \left(\dfrac{-x}{b}\right)
\Leftrightarrow \dfrac{x}{b}>\dfrac{-x}{b}
\Leftrightarrow x>0.
On en déduit alors que f^{\prime}(x)=0 \Leftrightarrow x=0 \text { et } f^{\prime}(x)>0 \Leftrightarrow x \lt 0.
La fonction f est donc croissante sur [-2 ; 0] et décroissante sur [0 ;2].
Pour s'entraîner
Exercices et p. 175
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

