Mathématiques 1re Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 6
TP / TICE 1
La méthode d'Euler pour tracer la courbe représentative de la fonction exponentielle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
On souhaite tracer la courbe représentative de la fonction exponentielle
en utilisant seulement sa définition : c'est l'unique fonction f
définie et dérivable sur \mathbb{R} telle que f' = f et f(0) = 1.
Question préliminaire :
1. Soit h > 0. Rappeler la définition du nombre dérivé de la fonction f en x = a .
2. Expliquer alors pourquoi on peut écrire que « très près de a » (on dit au voisinage de a ) : f(a+h) \approx f(a)+h f^{\prime}(a).
Question préliminaire :
1. Soit h > 0. Rappeler la définition du nombre dérivé de la fonction f en x = a .
2. Expliquer alors pourquoi on peut écrire que « très près de a » (on dit au voisinage de a ) : f(a+h) \approx f(a)+h f^{\prime}(a).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Construire point par point la courbe représentative
de la fonction exponentielle sur
l'intervalle [0 ; 1] à l'aide des segments
représentant des fonctions affines en
utilisant une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le segment [\text{AB}] représente une fonction affine sur l'intervalle [0 ; 0\text{,}4] et est
proche de la courbe représentant la fonction f telle que f(0)=1 et f'(0) = 1 avec h = 0{,}4.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1GeoGebra
On choisit de partager l'intervalle [0 ; 1] en dix intervalles
réguliers (appelés subdivision régulière).
1. a. Quel sera le pas h de la subdivision ?
b. En utilisant la définition de la fonction exponentielle et la question préliminaire 2. , donner une approximation affine de f(0{,}1).
c. Quelle est la valeur approximative de f'(0\text{,}1) ?
d. En déduire une approximation affine de f(0{,}2) .
b. En utilisant la définition de la fonction exponentielle et la question préliminaire 2. , donner une approximation affine de f(0{,}1).
c. Quelle est la valeur approximative de f'(0\text{,}1) ?
d. En déduire une approximation affine de f(0{,}2) .
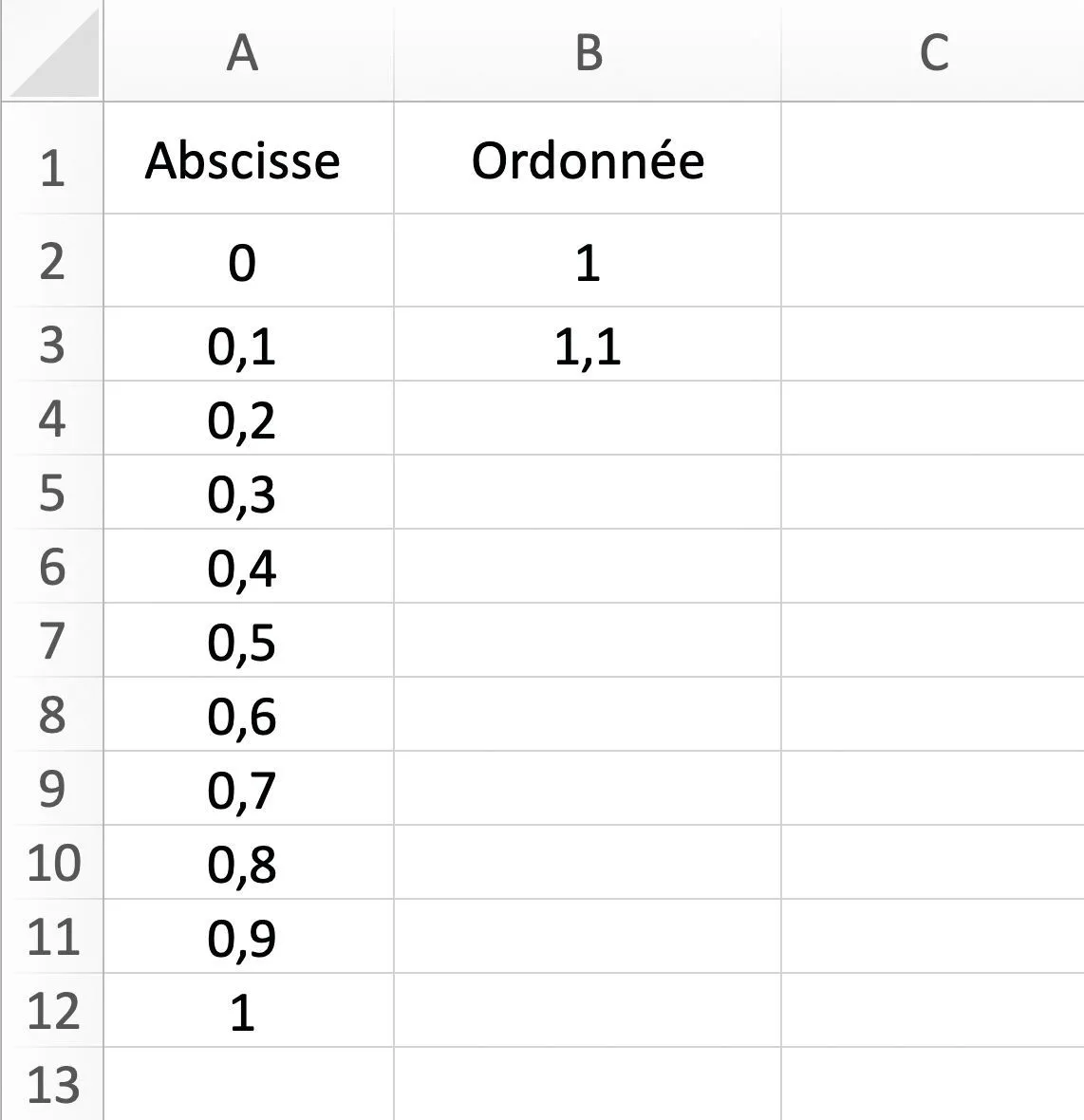
2. Construire une
feuille de tableur sur GeoGebra comme ci-dessus.
3. Représenter le nuage de points associé à cette feuille de calculs et tracer une courbe approximative de la fonction exponentielle sur l'intervalle [0 ; 1].
4. Comment obtenir une courbe plus précise ? Faire des essais.
GeoGebra
3. Représenter le nuage de points associé à cette feuille de calculs et tracer une courbe approximative de la fonction exponentielle sur l'intervalle [0 ; 1].
Cliquez ici pour avoir accès à un espace de dessin
4. Comment obtenir une courbe plus précise ? Faire des essais.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Python
On choisit de partager l'intervalle [0\, ; 1] en dix
intervalles réguliers (appelés subdivision régulière).
1. a. Quel sera le pas h de la subdivision ?
b. En utilisant la définition de la fonction exponentielle et la question préliminaire 2., donner une approximation affine de f(0\text{,}1) .
c. Quelle est la valeur approximative de f'(0{,}1) ?
d. En déduire une approximation affine de f(0{,}2) .
b. En utilisant la définition de la fonction exponentielle et la question préliminaire 2., donner une approximation affine de f(0\text{,}1) .
c. Quelle est la valeur approximative de f'(0{,}1) ?
d. En déduire une approximation affine de f(0{,}2) .
2. Le programme ci-dessous donne une courbe
approchant la représentation graphique de la
fonction exponentielle sur l'intervalle [0 ; 1]. Où
apparaît le nombre de subdivisions régulières ?
3. Expliquer le code des lignes 9 à 13.
4. Exécuter ce programme avec dix puis cent subdivisions et comparer le résultat avec la courbe de la fonction exponentielle.
from matplotlib import pyplot as plt n = 10 x = [] #liste des abscisses y = [] #liste des ordonnées x = x + [0] y = y + [1] for k in range(1, n + 1): a = float(x[k - 1]) + 1/n x = x + [a] b = (1 + 1/n)*float(y[k - 1]) y = y + [b] # Affichage des points dans le repère plt.clf() plt.plot(x, y, marker='o', linestyle='-') plt.show()
3. Expliquer le code des lignes 9 à 13.
4. Exécuter ce programme avec dix puis cent subdivisions et comparer le résultat avec la courbe de la fonction exponentielle.
Cliquez ici pour avoir accès à un espace de dessin
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
