Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 9
Activité
Produit scalaire
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AProjection orthogonale
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On considère une droite d du plan et un point \text{A} n'appartenant pas à cette droite. On rappelle que le projeté orthogonal du point \text{A} sur la droite d est le point \text{A}^ { \prime } appartenant à d tel que les droites d et \left( \mathrm { AA } ^ { \prime } \right) sont perpendiculaires.
a) Reproduire le quadrilatère et tracer les projetés orthogonaux des sommets \text{B} et \text{D} sur la droite \text{(AC)} ainsi que les projetés orthogonaux des sommets \text{A} et \text{C} sur la droite \text{(BD).}
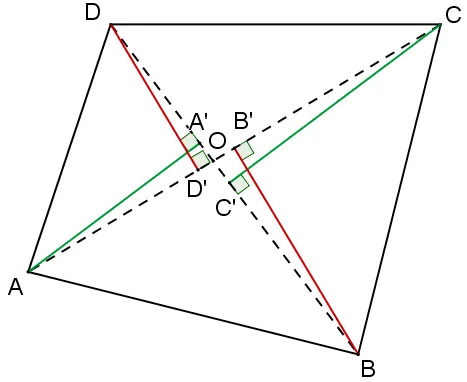
b) Donner deux exemples de quadrilatères où les quatre projetés orthogonaux obtenus de cette manière sont confondus. Justifier la réponse.
a) Construire l'ensemble des points \text{M} du plan tel que le projeté orthogonal de \text{M} sur la droite \text{(AC)} soit le point \text{O.}
b) Construire l'ensemble des points \text{N} du plan tel que le projeté orthogonal de \text{N} sur la droite \text{(BD)} soit le point \text{O.}
Dans chacun des cas suivants :
a) Les droites \text{(AB)} et d sont parallèles.
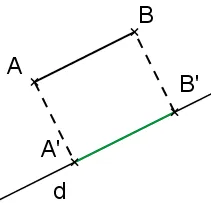
b) Les droites \text{(AB)} et d sont perpendiculaires.
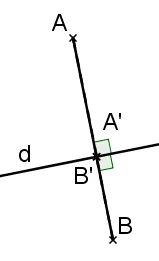
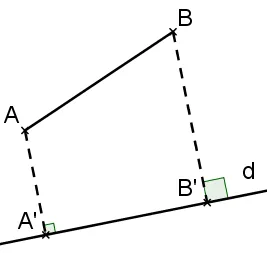
c) Les droites \text{(AB)} et d ne sont ni parallèles, ni perpendiculaires : dans ce cas, trouver et tracer les deux configurations possibles en fonction des positions des points \text{A} et \text{B} relativement à la droite d .
1
On considère ci-dessous le quadrilatère \text{ABCD} de centre \text{O.}
Le zoom est accessible dans la version Premium.
a) Reproduire le quadrilatère et tracer les projetés orthogonaux des sommets \text{B} et \text{D} sur la droite \text{(AC)} ainsi que les projetés orthogonaux des sommets \text{A} et \text{C} sur la droite \text{(BD).}
GeoGebra
Cliquez ici pour avoir accès à une correction
Le zoom est accessible dans la version Premium.
b) Donner deux exemples de quadrilatères où les quatre projetés orthogonaux obtenus de cette manière sont confondus. Justifier la réponse.
2
On considère maintenant des points distincts des quatre sommets du quadrilatère.
a) Construire l'ensemble des points \text{M} du plan tel que le projeté orthogonal de \text{M} sur la droite \text{(AC)} soit le point \text{O.}
b) Construire l'ensemble des points \text{N} du plan tel que le projeté orthogonal de \text{N} sur la droite \text{(BD)} soit le point \text{O.}
Aide
Si \text{O} est le projeté orthogonal de \text{M} sur la droite \text{(AC)}, quel lien existe-t-il entre les droites \text{(MO)} et \text{(AC)} ?
3
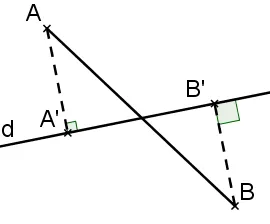
On change de configuration et on considère à présent une droite d et deux points distincts \text{A} et \text{B} n'appartenant pas à d. On note \mathrm { A } ^ { \prime } et \mathrm { B } ^ { \prime } les projetés orthogonaux respectifs des points \text{A} et \text{B} sur la droite d .
Le segment \left[ \mathrm { A } ^ { \prime } \mathrm { B } ^ { \prime } \right] est alors le projeté orthogonal du segment \text{[AB]} sur la droite d .Dans chacun des cas suivants :
- faire une figure ;
- tracer le segment \left[ \mathrm { A } ^ { \prime } \mathrm { B } ^ { \prime } \right] ;
- comparer les longueurs de \text{AB} et \text{A'B'.}
a) Les droites \text{(AB)} et d sont parallèles.
GeoGebra
Cliquez ici pour avoir accès à une correction
Le zoom est accessible dans la version Premium.
b) Les droites \text{(AB)} et d sont perpendiculaires.
GeoGebra
Cliquez ici pour avoir accès à une correction
Le zoom est accessible dans la version Premium.
c) Les droites \text{(AB)} et d ne sont ni parallèles, ni perpendiculaires : dans ce cas, trouver et tracer les deux configurations possibles en fonction des positions des points \text{A} et \text{B} relativement à la droite d .
Aide
On peut supposer que les points \text{A} et \text{B} sont du même côté de la droite d . Quelle est l'autre configuration possible ?
GeoGebra
Cliquez ici pour avoir accès à une correction
Le zoom est accessible dans la version Premium.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BilanDans la configuration de la question 3, pour quels cas a-t-on \text{AB} > \mathrm { A } ^ { \prime } \mathrm { B } ^ { \prime } , \text{AB} \lt \mathrm { A } ^ { \prime } \mathrm { B } ^ { \prime } et \text{AB} = \mathrm { A } ^ { \prime } \mathrm { B } ^ { \prime } ?
Bilan
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BDéfaut d'orthogonalité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Quelle est la valeur de \Delta si le triangle \text{ABC} est rectangle en \text{A} ?2
On suppose que l'angle (\overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{AC}}) est un angle aigu.
Aide
Utiliser le théorème de Pythagore dans les triangles rectangles \text{AHC} et \text{CHB} puis modifier l'expression de \Delta .
b) En utilisant plusieurs fois le théorème de Pythagore dans des triangles bien choisis, démontrer que\Delta=\mathrm{AB} \times \mathrm{AH}.
3
On suppose que l'angle (\overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{AC}}) est un angle obtus.Démontrer que \Delta=-\mathrm{AB} \times \mathrm{AH}.
Aide
Utiliser le théorème de Pythagore dans les triangles rectangles \text{AHC} et \text{CHB} puis modifier l'expression de \Delta .
4
a) Prouver que, dans les deux cas, \Delta=\mathrm{AB} \times \mathrm{AC} \times \cos (\overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{AC}}).b) Pourquoi parle-t-on alors de « défaut d'orthogonalité » ?
Aide
Utiliser les formules trigonométriques dans le triangle rectangle.
5
Justifier que \Delta=\dfrac{\|\overrightarrow{\mathrm{AB}}\|^{2}+\|\overrightarrow{\mathrm{AC}}\|^{2}-\| \overrightarrow{\mathrm{AC}}-\overrightarrow{\mathrm{AB}}\|^2}{2}.6
On se place dans un repère orthonormé (\text{O}\, ; \vec{i}, \vec{j}) et on considère les vecteurs \overrightarrow{\mathrm{AB}}\begin{pmatrix}{x} \\ {y}\end{pmatrix} et \overrightarrow{\mathrm{AC}}\begin{pmatrix}{x^{\prime}} \\ {y^{\prime}}\end{pmatrix}.Prouver, à l'aide de la formule précédente, que \Delta=x x^{\prime}+y y^{\prime}.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Bilan Lister les quatre différentes expressions de \Delta obtenues. Indiquer quelles données (coordonnées, longueurs, angles) sont nécessaires pour appliquer chacune des formules.
Bilan
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CLes différentes propriétés du produit scalaire
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Montrer que, pour tout réel k, \vec{u} \cdot(k \vec{v})=(k \vec{u}) \cdot \vec{v}=k(\vec{u} \cdot \vec{v}).
2
Montrer que \vec{u} \cdot(\vec{v}+\vec{w})=\vec{u} \cdot \vec{v}+\vec{u} \cdot \vec{w}.
3
Montrer que \vec{u} \cdot \vec{v}=\vec{v} \cdot \vec{u}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Bilan Quelle opération possède des propriétés analogues au produit scalaire ?
Bilan
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif : Se familiariser avec la projection orthogonale de segments sur des droites, après avoir étudié la projection orthogonale de points sur une droite en seconde.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif : Déterminer les différentes expressions du produit scalaire au travers d'une interprétation géométrique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
\text{ABC} est un triangle quelconque du plan. On note :
- \text{H} le projeté orthogonal du point \text{C} sur la droite \text{(AB)} ;
- \Delta le défaut d'orthogonalité du triangle \text{ABC} défini par \Delta=\dfrac{\mathrm{AB}^{2}+\mathrm{AC}^{2}-\mathrm{BC}^{2}}{2}.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif : L'objectif est de démontrer les différentes propriétés du produit scalaire en utilisant sa forme analytique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Dans un repère orthonormé (\text{O}\, ; \vec{i}, \vec{j}) du plan, on considère les vecteurs \vec{u}\begin{pmatrix}{x_{1}} \\ {y_{1}}\end{pmatrix}, \vec{v}\begin{pmatrix}{x_{2}} \\ {y_{2}}\end{pmatrix} et \vec{w}\begin{pmatrix}{x_{3}} \\ {y_{3}}\end{pmatrix}.
Répondre aux questions suivantes en se servant de la formule du produit scalaire utilisant les coordonnées de vecteurs.
Répondre aux questions suivantes en se servant de la formule du produit scalaire utilisant les coordonnées de vecteurs.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah