Mathématiques 1re Spécialité
Mes Pages
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 9
Produit scalaire
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Capacités attendues
1. Calculer le produit scalaire de deux vecteurs en choisissant une méthode adaptée.
2. Utiliser le produit scalaire pour démontrer une orthogonalité, calculer un angle ou une longueur.
3. Faire le lien entre équation cartésienne de droite et vecteur normal.
2. Utiliser le produit scalaire pour démontrer une orthogonalité, calculer un angle ou une longueur.
3. Faire le lien entre équation cartésienne de droite et vecteur normal.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le produit scalaire est un outil utilisé en infographie pour la réalisation de décors en trois dimensions. Il permet, par exemple, de délimiter le champ de vision d'un personnage, ainsi que les faces visibles de bâtiments ou d'objets qu'il faudra créer en conséquence.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Avant de commencer
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Prérequis
1. Calculer la norme d'un vecteur.
2. Travailler avec des coordonnées.
3. Connaître les valeurs remarquables du sinus et du cosinus.
4. Tracer le projeté orthogonal d'un point sur une droite.
5. Vérifier l'appartenance d'un point à une droite.
6. Faire le lien entre équation cartésienne de droite et vecteur directeur.
7. Utiliser la relation de Chasles.
3. Connaître les valeurs remarquables du sinus et du cosinus.
4. Tracer le projeté orthogonal d'un point sur une droite.
5. Vérifier l'appartenance d'un point à une droite.
6. Faire le lien entre équation cartésienne de droite et vecteur directeur.
7. Utiliser la relation de Chasles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
L'origine du produit scalaire remonte à la création des quaternions (nombres de dimension 4) par le mathématicien irlandais Sir William Rowan Hamilton, en 1843. La première composante d'un quaternion est appelée la composante scalaire et les trois autres sont appelées les composantes vectorielles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Calculer des normes de vecteurs
On considère, dans un repère orthonormé, les vecteurs \vec{u}\left(\begin{array}{l}{1} \\ {4}\end{array}\right) et \vec{v}\left(\begin{array}{c}{-3} \\ {2}\end{array}\right).
Calculer les coordonnées et les normes des vecteurs suivants. 1. \vec{v}-\vec{u}
Calculer les coordonnées et les normes des vecteurs suivants. 1. \vec{v}-\vec{u}
2. 3 \vec{u}+\vec{v}
3. \vec{u}+\sqrt{2} \times \vec{v}
3. \vec{u}+\sqrt{2} \times \vec{v}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Déterminer des coordonnées de vecteurs
Dans le carré \text{ABCD} est inscrit le triangle équilatéral \text{ABE.} \text{I} est le milieu du segment \text{[AB].}
Quelles sont les coordonnées des vecteurs suivants dans le repère (\mathrm{A} ; \overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{AD}}) ?
Quelles sont les coordonnées des vecteurs suivants dans le repère (\mathrm{A} ; \overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{AD}}) ?
1. \overrightarrow{\mathrm{DC}}
2. \overrightarrow{\mathrm{BI}}
3. \overrightarrow{\mathrm{AC}}
2. \overrightarrow{\mathrm{BI}}
3. \overrightarrow{\mathrm{AC}}
4. \overrightarrow{\mathrm{AE}}
5. \overrightarrow{\mathrm{DE}}
5. \overrightarrow{\mathrm{DE}}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Connaître les valeurs remarquables
Compléter le tableau des valeurs remarquables du sinus et du cosinus.
| x | \sin(x) | \cos(x) |
| 0 | ||
| \dfrac{\pi}{6} | ||
| \dfrac{\pi}{4} | ||
| \dfrac{\pi}{3} | ||
| \dfrac{\pi}{2} | ||
| \pi |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Utiliser le projeté orthogonal d'un point
1. Tracer le triangle \text{ABC} tel que \text{AB} = 5 cm, \text{AC} = 10 cm et \widehat{\mathrm{BAC}}=30^{\circ}.
GeoGebra
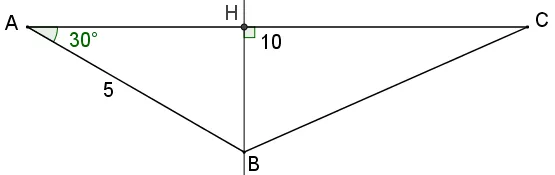
Cliquez ici pour avoir accès à une correction
2. a. Construire le point \text{H}, projeté orthogonal de \text{B} sur la droite \text{(AC).}
b. Que représente la droite (\text{BH}) \:?
3. a. Calculer les valeurs exactes des longueurs \text{BH} et \text{AH.}
b. Calculer la valeur exacte de l'aire du triangle \text{ABC.}
b. Que représente la droite (\text{BH}) \:?
3. a. Calculer les valeurs exactes des longueurs \text{BH} et \text{AH.}
b. Calculer la valeur exacte de l'aire du triangle \text{ABC.}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
Utiliser une équation de droite
On considère le point \text{A}(-2\, ; 3). Dans chaque cas, déterminer si le point \text{A} appartient à la droite donnée.
1. Droite d_1 d'équation 8 x-2 y+10=0.
2. Droite d_2 d'équation 7 y+3 x-15=0.
3. Droite d_3 d'équation \dfrac{1}{2} x=4 y-5.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
Problème
Soit \text{ABCD} un parallélogramme. Le point \text{E} est tel que \overrightarrow{\mathrm{DC}}=\overrightarrow{\mathrm{CE}}, le point \text{F} tel que \overrightarrow{\mathrm{DF}}=2 \overrightarrow{\mathrm{DA}} et le point \text{G} tel que \overrightarrow{\mathrm{BG}}=\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{DE}}.
1. Construire la figure correspondante.
Cliquez ici pour avoir accès à un espace de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
Déterminer un vecteur directeur
Déterminer un vecteur directeur de chacune des droites suivantes.
1. Droite d_1 d'équation 3 x-4 y+5=0.
2. Droite d_2 d'équation 7 y-9 x=2.
3. Droite d_3 d'équation x=-2 y.
4. Droite d_4 d'équation \dfrac{2}{3} y+\dfrac{3}{4}=0.
5. Droite d_5 passant par les points \mathrm{A}(2\, ;-4) et \mathrm{B}(-1\, ;-5).
6. Droite d_6 verticale.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
