Partie 3
Histoire des mathématiques
Géométrie
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
HistoireL'avènement du produit scalaire
La notion de vecteur était implicite depuis Galilée mais, à l'époque, sa forme était différente de celle que nous connaissons actuellement. Dans son livre Philosophiae Naturalis Principia Mathematica (1687), Newton décrit les règles de calcul à appliquer aux forces. Parallèlement, la notion de vecteur apparaît chez Leibniz au cours de ses recherches sur l'élaboration d'un calcul des variations, créant un lien entre analyse et géométrie. Au XIXe siècle, les scientifiques et les ingénieurs, comme Willard Gibbs (1839-1903), utilisent ces notions mais ont besoin d'outils encore plus performants, comme pour calculer le travail d'une force : ce sera la naissance du produit scalaire. Les nouveaux outils vectoriels alors mis en place permettront une approche différente de la géométrie jusque-là utilisée, avec l'avantage de combiner vision géométrique et calculs.


Extrait de Elements of Vector Analysis Arranged for the Use of Students in Physics, de Josiah Willard Gibbs, 1881.
Willard Gibbs était un ingénieur, physicien et mathématicien. Il travaillait sur l'application de la thermodynamique à la chimie. Pour ses propres besoins de recherche, notamment en astronomie ou pour ses études sur la lumière, il utilisait le calcul vectoriel qu'il enseignait comme élément d'analyse vectorielle (voir l'extrait) y apportant, entre autres, la notation « · » pour le produit scalaire.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
HistoireÉquation d'une courbe


Avant l'avènement du calcul littéral, une courbe était définie par des conditions sur ses points. Par exemple, un cercle était l'ensemble des points du plan équidistants d'un point donné (centre du cercle). Les travaux de René Descartes (1596-1650), publiés dans la partie La Géométrie du Discours de la méthode (1637), permettent de définir une courbe par une équation qui lie les coordonnées des points de cette courbe. Dans un repère orthonormé de centre O, le cercle de centre O et de rayon 1 devient alors la courbe ayant pour équation x^2 + y^2 = 1 .

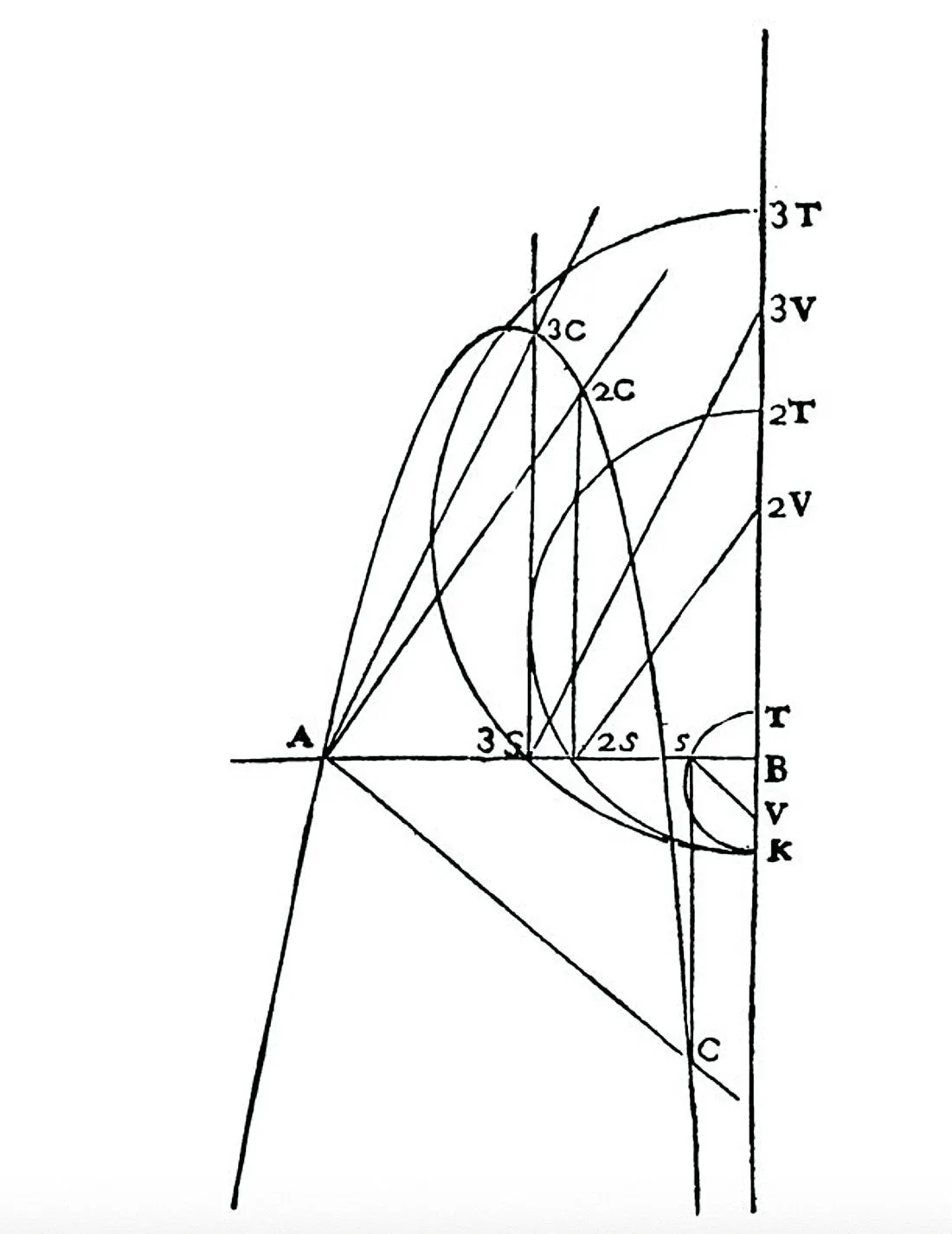
Parabole et repère - La Géométrie, Discours de la méthode.


Maria Gaetana Agnesi (1718-1799) est la première mathématicienne de l'Histoire nommée professeure d'université (Bologne, Italie). À l'âge de neuf ans, elle rédige un discours sur le droit des filles à l'éducation supérieure. Elle publie en 1748 les Istituzioni Analitiche, traité renommé pour sa clarté et l'unité de sa méthode. Elle utilise le calcul différentiel (encore en pleine élaboration) pour l'étude de courbes, dont la cubique d'Agnesi (plus connue sous le nom de « sorcière d'Agnesi »). Son équation est : y^2x = a^2 (a - x) .

La cubique d'Agnesi (courbe rouge).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
1. Dans un repère orthonormé d'origine \text{O}, montrer qu'un point \text{M}(x\, ; y) appartient au cercle de centre \text{O} et de rayon 1 si et seulement si x^2 + y^2 = 1 .
2. À partir de la représentation de la cubique d'Agnesi, essayer de retrouver comment la définir point par point.
2. À partir de la représentation de la cubique d'Agnesi, essayer de retrouver comment la définir point par point.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

