Chapitre 9
TP / TICE 1
Rechercher une situation d'orthogonalité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
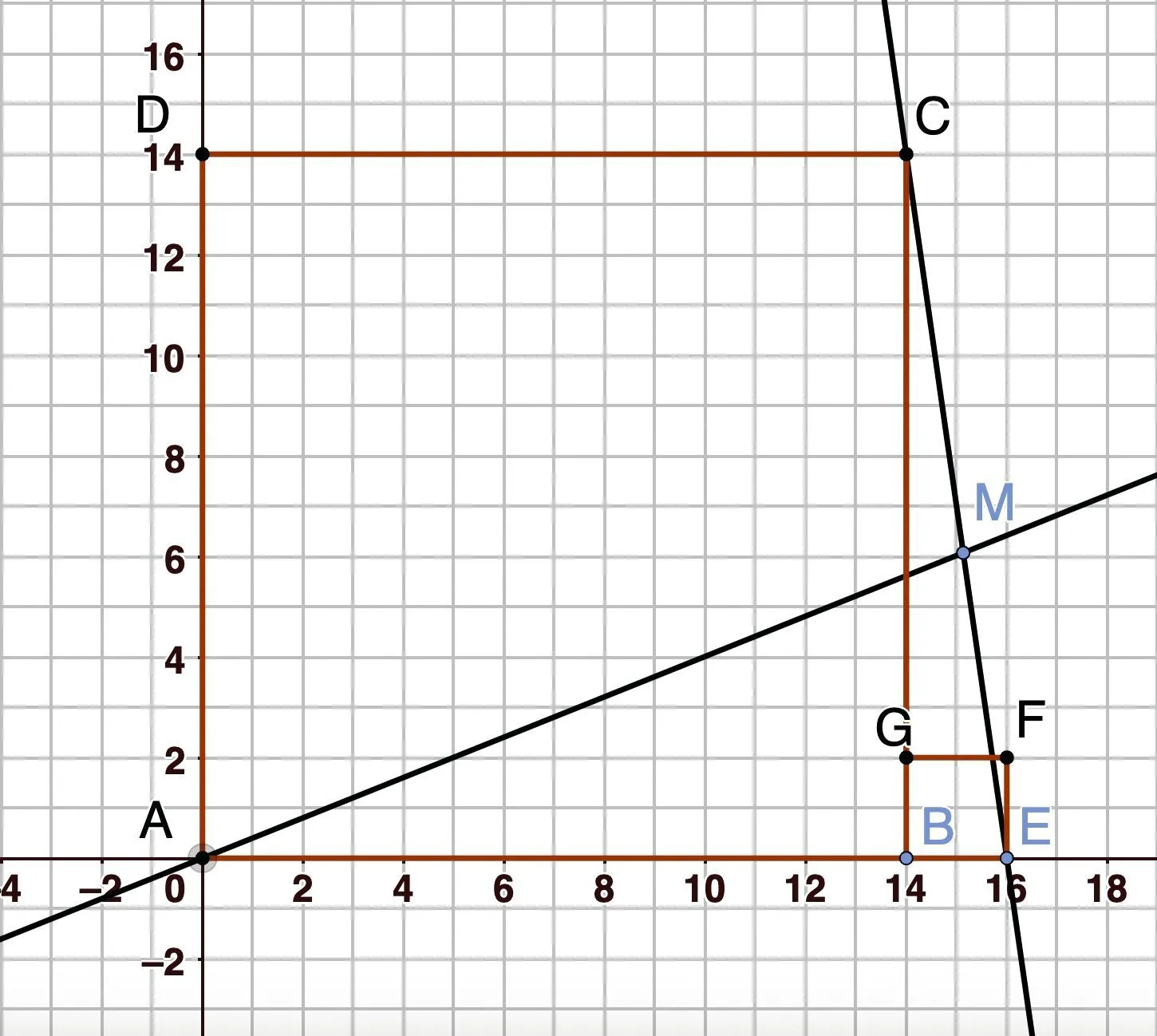
Soit \text{ABCD} un carré de côté de longueur b et \text{BEFG} un carré de longueur e à l'extérieur du premier tel que \text{G} \in [\text{CB}]. Soit \text{M} un point appartenant à la droite (\text{CE}).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
En utilisant une des deux méthodes, trouver la position du point \mathbf{M}\left(x_{\mathbf{M}} \: ; y_{\mathbf{M}}\right) pour que les droites (\text{AM}) et (\text{CE}) soient perpendiculaires.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1GeoGebra
1. À l'aide de l'outil Polygone régulier, tracer le carré \text{ABCD} de façon à ce que les points \text{A} et \text{B} aient pour coordonnées respectives (0\, ; 0) et (14\, ; 0).
Tracer de la même manière le carré \text{BEFG} de façon à ce que \text{E} ait pour coordonnées (16\, ; 0).
Tracer de la même manière le carré \text{BEFG} de façon à ce que \text{E} ait pour coordonnées (16\, ; 0).
2. Avec l'outil Droite, tracer la droite (\text{CE}) et ajouter un point mobile \text{M} sur cette droite.
3. Tracer la droite (\text{AM}).

3. Tracer la droite (\text{AM}).


4. Dans la barre de saisie, afficher la valeur du produit scalaire \overrightarrow{\mathrm{MA}} \cdot \overrightarrow{\mathrm{ME}} avec la commande :
5. Trouver l'emplacement du point \text{M} tel que \overrightarrow{\mathrm{MA}} \cdot \overrightarrow{\mathrm{ME}}=0. Il est possible de zoomer sur la figure pour effectuer des déplacements plus précis.
6. Conjecturer l'emplacement du point \text{G} par rapport à la droite (\text{AM}) .
7. Changer les dimensions des carrés \text{ABCD} et \text{BEFG} et reprendre les questions 5. et 6..
ProduitScalaire( < Vecteur >, < Vecteur >)
5. Trouver l'emplacement du point \text{M} tel que \overrightarrow{\mathrm{MA}} \cdot \overrightarrow{\mathrm{ME}}=0. Il est possible de zoomer sur la figure pour effectuer des déplacements plus précis.
6. Conjecturer l'emplacement du point \text{G} par rapport à la droite (\text{AM}) .
7. Changer les dimensions des carrés \text{ABCD} et \text{BEFG} et reprendre les questions 5. et 6..
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Tableur
On se place dans le repère orthonormé (\mathrm{A}\, ; \vec{i}, \vec{j}) tel que \vec{i} est colinéaire à \overrightarrow{\text{AB}} et \vec{j} est colinéaire à \overrightarrow{\text{AD.}} On se place dans le cas où b > e .
2. On pose \overrightarrow{\mathrm{AM}}=\overrightarrow{\mathrm{AE}}+\overrightarrow{k \mathrm{EC}} avec k \in[0\, ; 1] Que peut-on dire du point \text{M} par rapport à la droite (\text{CE}) ?
Exprimer le produit scalaire \overrightarrow{\mathrm{AM}} \cdot \overrightarrow{\mathrm{CE}} en fonction de b , e et k .
3. On considère le cas où b = 14 et e = 2 . Dans une feuille de calcul, lister dans la première colonne les valeurs de k avec un pas de 0{,}01 et dans la deuxième colonne les valeurs de \overrightarrow{\mathrm{AM}} \cdot \overrightarrow{\mathrm{CE}} correspondantes. Quelle est la valeur de k pour laquelle \overrightarrow{\mathrm{AM}} \cdot \overrightarrow{\mathrm{CE}}=0 ?
4. Que peut-on dire des droites (\text{AM}) et (\text{CE}) pour cette valeur de k ?
5. Exprimer à l'aide de la question 2. les coordonnées du point \text{M} ainsi que les distances \text{AG}, \text{AM} et \text{GM} en fonction de b , e et k . Calculer ces valeurs pour la valeur de k trouvée à la question 3. .
6. Que vaut la valeur \text{AG} + \text{GM}- \text{AM} ? Que peut-on en déduire pour les points \text{A}, \text{G} et \text{M} ?
5. Exprimer à l'aide de la question 2. les coordonnées du point \text{M} ainsi que les distances \text{AG}, \text{AM} et \text{GM} en fonction de b , e et k . Calculer ces valeurs pour la valeur de k trouvée à la question 3. .
6. Que vaut la valeur \text{AG} + \text{GM}- \text{AM} ? Que peut-on en déduire pour les points \text{A}, \text{G} et \text{M} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. En utilisant le produit scalaire \overrightarrow{\mathrm{CE}} \cdot \overrightarrow{\mathrm{AM}}, trouver une condition sur les coordonnées de \text{M} lorsque (\text{AM}) et (\text{CE}) sont perpendiculaires.
2. Déterminer une équation cartésienne de la droite (\text{AM}) .
3. Démontrer que le point \text{G} appartient à la droite (\text{AM}) pour toutes valeurs de b et e strictement positives.
2. Déterminer une équation cartésienne de la droite (\text{AM}) .
3. Démontrer que le point \text{G} appartient à la droite (\text{AM}) pour toutes valeurs de b et e strictement positives.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

