35
[Modéliser.]
On a demandé à 180 élèves s'ils étaient demi-pensionnaires ou internes ainsi que la langue vivante étudiée hormis l'anglais (espagnol ou allemand). On choisit un élève au hasard.
On note \text{A} l'événement « l'élève apprend l'allemand », \text{E} : « l'élève apprend l'espagnol » et \text{I} « l'élève est interne ».

1. Compléter le tableau suivant.

	Allemand	Espagnol	Total
DP			100
Interne		50
Total	40		180

2. a. Calculer \text{P(A) } et \mathrm{P}(\mathrm{A} \cap \mathrm{I}).

b. En déduire \mathrm{P_{A}(I)} et interpréter le résultat par une phrase.

3. Calculer la probabilité d'obtenir un élève interne sachant qu'il apprend l'espagnol.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

36
[Calculer.]

On considère deux événements \text{A} et \text{B} dont les probabilités sont données dans le tableau suivant.

	\text{A}	\overline{\mathrm{A}}	Total
\text{B}	0,3
\overline{\mathrm{B}}			0,6
Total		0,6

1. Compléter le tableau.
2. Calculer \mathrm{P_{A}(B)} et \mathrm{P_{B}(\overline{A})}.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

37
[Raisonner.]
On suppose que \text{A} et \text{B} sont deux événements de probabilité non nulle.

Établir que \mathrm{P}_{\mathrm{A}}(\mathrm{B}) \times\left(\dfrac{1}{\mathrm{P}_{\mathrm{B}}(\mathrm{A})}-1\right)=\dfrac{\mathrm{P}(\mathrm{A} \cup \mathrm{B})}{\mathrm{P}(\mathrm{A})}-1.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

38
[Calculer.]

Soient \text{A} et \text{B} deux événements tels que \mathrm{P_{A}(B) = 0\text{,}8} et \mathrm{P_{B}(A) = 0\text{,}6} et \mathrm{P(A) = 0{,}4.}

1. Calculer \mathrm{P}(\mathrm{A} \cap \mathrm{B}).

2. En déduire \mathrm{P(B)}.

3. Calculer alors \mathrm{P(A \cup B).}

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

39
[Calculer.]
Soient deux événements \text{A} et \text{B} tels que \mathrm{P(A) = 0\text{,}8, P(B) = 0\text{,}7, } \mathrm{P}(\mathrm{A} \cap \overline{\mathrm{B}})=0\text{,}15 et \mathrm{P}(\overline{\mathrm{A}} \cap \mathrm{B})=0\text{,}05.

1. Calculer \mathrm{P (A \cap B)}.

2. En déduire \mathrm{P_{B}(A).}

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

40
[Calculer.]
On lance un dé équilibré à six faces et on considère les événements \text{A} : « obtenir 4 ; 5 ou 6 » et \text{B} : « obtenir un nombre pair ».

1. Calculer \mathrm{P_{B}(A).}

2. Calculer \mathrm{P_{A}(B)}.

3. Calculer \mathrm{P_{A \cap B}(A \cup B).}

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

41
[Calculer.]
On considère deux événements \text{A} et \text{B} et l'arbre de probabilité ci-dessous.

Le zoom est accessible dans la version Premium.

1. Compléter cet arbre pondéré.
2. Quelle est la probabilité que \text{B} se réalise sachant que \text{A} n'est pas réalisé ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

42
[Représenter.]
Soient \text{A} et \text{B} deux événements dont on donne les probabilités dans le tableau suivant.

	\text{B}	\overline{\mathrm{B}}	Total
\text{A}	0,16		0,64
\overline{\mathrm{A}}
Total	0,48

1. Compléter le tableau.
2. En déduire les probabilités \mathrm{P_{A}(B)} et \mathrm{P_{\overline{A}}(B)}.

3. Représenter cette situation à l'aide d'un arbre pondéré.

Cliquez pour accéder à une zone de dessin

Cette fonctionnalité est accessible dans la version Premium.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

43
[Modéliser.]

Dans une forêt, il y a 30 % d'épicéas et 70 % de sapins. 10% des arbres ont un parasite. Les épicéas représentent 20 % des arbres touchés.

Le zoom est accessible dans la version Premium.

Quelle est la probabilité qu'un épicéa soit touché par le parasite ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

44
[Calculer.]
Dans la trousse de Sophie, il y a quinze crayons indiscernables au toucher. Cinq sont noirs, trois sont blancs, quatre sont rouges et trois sont verts. Elle choisit au hasard un crayon. Chaque crayon a la même probabilité d'être choisi.

1. Quelle est la probabilité qu'elle choisisse un crayon noir ?

2. Quelle est la probabilité qu'elle choisisse un crayon vert sachant que l'événement « elle n'a pas tiré un crayon noir » est réalisé ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

45
[Chercher.]
Raphaël consulte les températures de la semaine prochaine et obtient le tableau ci-dessous.

L	M	M	J	V	S	D
16 °	23 °	21 °	18 °	14 °	13 °	14 °

Il choisit une journée au hasard pour aller faire du vélo. On suppose que chaque journée à la même probabilité d'être choisie.

1. Quelle est la probabilité de choisir un jour où la température est supérieure à 15 °C sachant qu'elle est inférieure à 20 °C ?

2. Quelle est la probabilité de choisir un jour où la température est inférieure à 20 °C sachant qu'elle est supérieure à 15 °C ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

46
[Modéliser.]

Vincent et Anne sont haltérophiles. La probabilité que Vincent soulève plus de 100 kg est égale à 0,75, alors que la probabilité qu'Anne soulève plus de 100 kg est égale à 0,6. La probabilité qu'au moins l'un des deux soulève plus de 100 kg est égale à 0,85.

Le zoom est accessible dans la version Premium.

1. Quelle est la probabilité qu'ils soulèvent 100 kg tous les deux ?

2. Anne vient de voir Vincent soulever 100 kg. Quelle est la probabilité qu'elle-même soulève 100 kg ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

47
[Chercher.]

On choisit au hasard une figure. Chaque figure a la même probabilité d'être choisie.

On considère les événements suivants :

\text{V} : « la figure est verte » ;

\text{R} : « la figure est rouge » ;

\text{N} : « la figure est noire » ;

\text{B} : « la figure est bleue » ;

\text{C} : « la figure est un cercle » ;

\text{K} : « la figure est un carré » ;

\text{Z} : « la figure fait des vagues ».

Le zoom est accessible dans la version Premium.

1. Modéliser cette situation par un tableau.

	C	K	Z	Total
N
V
R
B
Total

2. Calculer \mathrm{P_{C}(V)} et \mathrm{P_{B}(Z)}.

3. Calculer \mathrm{P_{R}(Z)} et \mathrm{P_{K}(B).}

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

48
[Modéliser.]
Un algorithme de détection de fraudes a été rédigé. Parmi toutes les fraudes, il en détecte 80 %. Il détecte un problème sur 10 % des dossiers étudiés et, parmi les cas qu'il détecte, 50 % sont effectivement des fraudes.

1. Calculer la probabilité qu'un dossier soit détecté et frauduleux.

2. En déduire la probabilité qu'un dossier soit frauduleux.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

49
[Modéliser.]

On considère le dessin ci-après constitué de quatre carrés de même dimension.
On dit que deux carrés sont adjacents s'ils se touchent par l'un de leurs côtés.
Par exemple, les carrés \text{1} et \text{2} sont adjacents au carré \text{0} mais pas le carré \text{3}.

Le zoom est accessible dans la version Premium.

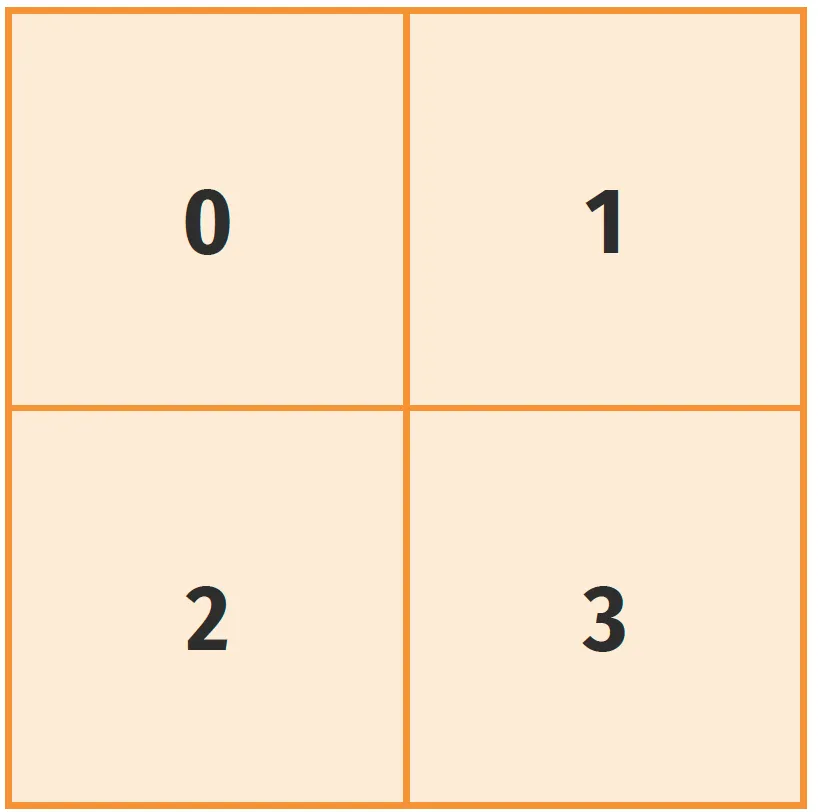
À l'étape 1, le carré 0 est noir. Les autres sont blancs. Au début de l'étape 2 et de toutes les étapes suivantes, un carré devient ou reste noir avec une probabilité de 0\text{,}5 si au moins l'un de ses voisins est noir. Cette probabilité est égale à 0\text{,}1 si aucun de ses voisins n'est noir.

Réaliser une simulation pour calculer la probabilité que le carré 3 soit noir lors de l'étape 3.

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

Oups, une coquille

j'ai une idée !

Nous préparons votre pageNous vous offrons 5 essais

Yolène

Émilie

Jean-Paul

Fatima

Sarah

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.