Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 12
TP / TICE 3
Convergence de la moyenne vers l'espérance
18 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Étudier la distance entre la moyenne d'un échantillon simulé de taille n
de la variable aléatoire \text{X} et \text{E(X)} à l'aide d'une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Une société d'assurance a réparti les sinistres en différentes catégories en fonction des montants à rembourser et de la probabilité théorique que ce sinistre intervienne. Voici le résumé réalisé :
Questions préliminaires :
1. Donner une interprétation de la colonne contenant 1\: 200.
2. On définit la variable aléatoire réelle \text{X} qui prend comme valeurs les montants des sinistres ci-dessus. Quel est le lien entre la variable aléatoire \text{X} et le tableau réalisé par la société d'assurance ?
3. Calculer et interpréter \text{E(X).}
| Montant du sinistre en € | 300 | 600 | 1 200 | 2 400 | 4 800 |
| Probabilité | 52,7 % | 16,4 % | 21,8 % | 5,5 % | 3,6 % |
Questions préliminaires :
1. Donner une interprétation de la colonne contenant 1\: 200.
2. On définit la variable aléatoire réelle \text{X} qui prend comme valeurs les montants des sinistres ci-dessus. Quel est le lien entre la variable aléatoire \text{X} et le tableau réalisé par la société d'assurance ?
3. Calculer et interpréter \text{E(X).}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Tableur
Le zoom est accessible dans la version Premium.
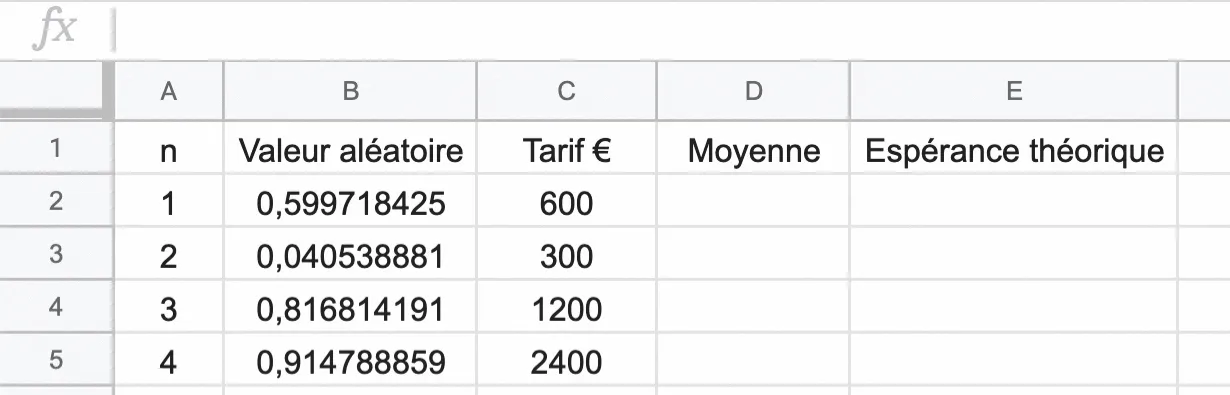
1. a. Que permet de faire l'instruction ALEA() sur le tableur ?
b. Dans la cellule B2, on a écrit =ALEA(). Expliquer pourquoi l'instruction suivante permet de simuler l'événement \{ \mathrm { X } = 300 \} avec la bonne probabilité : =SI(B2 <= 0,527 ; 300 ; …).
c. Que faut-il indiquer comme instruction utilisant la fonction ET et la cellule B2 pour obtenir le résultat 600 dans la cellule C2 ?
2. Comment expliquer la saisie finale effectuée dans la cellule C2 ?
b. Dans la cellule B2, on a écrit =ALEA(). Expliquer pourquoi l'instruction suivante permet de simuler l'événement \{ \mathrm { X } = 300 \} avec la bonne probabilité : =SI(B2 <= 0,527 ; 300 ; …).
c. Que faut-il indiquer comme instruction utilisant la fonction ET et la cellule B2 pour obtenir le résultat 600 dans la cellule C2 ?
2. Comment expliquer la saisie finale effectuée dans la cellule C2 ?
Le zoom est accessible dans la version Premium.
3. a. En utilisant les formules ci-dessus, simuler un échantillon de taille n = 10 : dix valeurs aléatoires entre 0 et 1 sont placées dans la colonne B et on leur associe la bonne valeur du sinistre dans la colonne C.
b. Calculer la moyenne des dix valeurs obtenues dans la colonne C.
c. Calculer la valeur absolue de la différence entre l'espérance théorique et la moyenne observée.
4. Reprendre la question 3. avec n = 100 , puis n = 1\:000 , puis n = 5\:000 . Que constate-t-on ?
b. Calculer la moyenne des dix valeurs obtenues dans la colonne C.
c. Calculer la valeur absolue de la différence entre l'espérance théorique et la moyenne observée.
4. Reprendre la question 3. avec n = 100 , puis n = 1\:000 , puis n = 5\:000 . Que constate-t-on ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Python
1. Importer la bibliothèque random qui permet d'utiliser l'instruction random(). À quoi sert cette instruction ?
2. a. Pour chaque échantillon simulé, on veut compter le nombre de sinistres pour chacun des montants. Créer alors cinq compteurs x_1, x_2, x_3, x_4 et x_5 initialisés à 0.
b. En quoi les instructions suivantes permettent de simuler l'événement \{ \text{X} = 300 \} avec la bonne probabilité ?
c. Quelle inégalité faut-il écrire sur a pour simuler l'événement \{ \text{X} = 600 \} ?
3. Écrire un programme complet qui permet de simuler les cinq montants possibles d'un sinistre.
4. a. Réaliser la simulation d'un échantillon de taille n = 10 et calculer la moyenne des valeurs obtenues.
b. Calculer la valeur absolue de la différence entre l'espérance théorique et la moyenne observée.
5. Reprendre la question 4. avec n = 100 , n = 1\:000 et n = 100\:000 . Que constate-t-on ?
2. a. Pour chaque échantillon simulé, on veut compter le nombre de sinistres pour chacun des montants. Créer alors cinq compteurs x_1, x_2, x_3, x_4 et x_5 initialisés à 0.
b. En quoi les instructions suivantes permettent de simuler l'événement \{ \text{X} = 300 \} avec la bonne probabilité ?
Le zoom est accessible dans la version Premium.
c. Quelle inégalité faut-il écrire sur a pour simuler l'événement \{ \text{X} = 600 \} ?
3. Écrire un programme complet qui permet de simuler les cinq montants possibles d'un sinistre.
4. a. Réaliser la simulation d'un échantillon de taille n = 10 et calculer la moyenne des valeurs obtenues.
b. Calculer la valeur absolue de la différence entre l'espérance théorique et la moyenne observée.
5. Reprendre la question 4. avec n = 100 , n = 1\:000 et n = 100\:000 . Que constate-t-on ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah