Chapitre 12
Préparer le bac
Probabilités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Exercice guidé
[D'après Bac S - Antilles-Guyane - 2018.]
L'exploitant d'une forêt communale décide d'abattre des arbres afin de les vendre, soit aux habitants de
la commune, soit à des entreprises. On admet que :
Parmi les arbres abattus, on en choisit un au hasard. On considère les événements suivants :
- parmi les arbres abattus, 30 % sont des chênes, 50 % sont des sapins et les autres sont des arbres d'essence secondaire (ce qui signifie qu'ils sont de moindre valeur) ;
- 45\text{,}9 % des chênes et 80 % des sapins abattus sont vendus aux habitants de la commune ;
- les trois quarts des arbres d'essence secondaire abattus sont vendus à des entreprises.
Parmi les arbres abattus, on en choisit un au hasard. On considère les événements suivants :
- \text{C} : « l'arbre abattu est un chêne » ;
- \text{S} : « l'arbre abattu est un sapin » ;
- \text{E} : « l'arbre abattu est un arbre d'essence secondaire » ;
- \text{H} : « l'arbre abattu est vendu à un habitant de la commune ».
1. Construire un arbre pondéré complet traduisant la situation.
Cliquez pour accéder à une zone de dessin
Aide
Avant de construire l'arbre, il faut se demander quel événement est représenté en premier. Faut-il d'abord considérer le type des arbres ou les personnes à qui on les vend ?
2. Calculer la probabilité que l'arbre abattu soit un chêne vendu à un habitant de la commune.
3. Justifier que la probabilité que l'arbre abattu soit vendu à un habitant de la commune est égale à 0\text{,}587\:7.
Aide
Il faut calculer une probabilité en utilisant une formule. Il faut commencer par écrire l'événement réalisé
mathématiquement en utilisant \text{C} et \text{H}.
3. Justifier que la probabilité que l'arbre abattu soit vendu à un habitant de la commune est égale à 0\text{,}587\:7.
Aide
On attend ici une justification et donc une démonstration. Comme souvent, pour les probabilités du lycée, cela passe par le calcul. Il faut repérer tous les chemins de l'arbre qui mènent à \text{H} et utiliser la formule des probabilités totales.
4. Quelle est la probabilité qu'un arbre abattu vendu à un habitant de la commune soit un sapin ? On donnera le résultat arrondi à 10^{-3}.
Aide
Il faut calculer la probabilité d'un événement sachant
qu'un événement connu s'est réalisé. Il s'agit donc de calculer une probabilité conditionnelle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
[D'après Bac S - Pondichéry - 2018.]
Une entreprise conditionne du sucre blanc provenant de deux exploitations \text{U} et \text{V} en paquets de 1 kg et de différentes qualités. Le sucre extra-fin est conditionné séparément dans des paquets portant le label « extra-fin ». Dans tout l'exercice, les résultats seront arrondis, si nécessaire, au millième. On sait que 3 % du sucre provenant de l'exploitation \text{U} est extra-fin et que 5 % du sucre provenant de l'exploitation \text{V} est extra-fin.
On prélève au hasard un paquet de sucre dans la production de l'entreprise et, dans un souci de traçabilité, on s'intéresse à la provenance de ce paquet. On considère les événements suivants :
On prélève au hasard un paquet de sucre dans la production de l'entreprise et, dans un souci de traçabilité, on s'intéresse à la provenance de ce paquet. On considère les événements suivants :
- \text{U} : « le paquet contient du sucre provenant de l'exploitation \text{U} » ;
- \text{V} : « le paquet contient du sucre provenant de l'exploitation \text{V} » ;
- \text{E} : « le paquet porte le label “extra-fin” ».
1. Dans cette question, on admet que l'entreprise
fabrique 30 % de ses paquets avec du sucre provenant de l'exploitation \text{U} et les autres avec du sucre provenant de l'exploitation \text{V,} sans mélanger les sucres des deux exploitations.
a. Quelle est la probabilité que le paquet prélevé porte le label « extra-fin » ?
b. Sachant qu'un paquet porte le label « extra-fin », quelle est la probabilité que le sucre qu'il contient provienne de l'exploitation \text{U}\: ?
a. Quelle est la probabilité que le paquet prélevé porte le label « extra-fin » ?
b. Sachant qu'un paquet porte le label « extra-fin », quelle est la probabilité que le sucre qu'il contient provienne de l'exploitation \text{U}\: ?
2. L'entreprise souhaite modifier son approvisionnement auprès des deux exploitations afin que, parmi les paquets portant le label « extra-fin », 30 % d'entre eux contiennent du sucre provenant de l'exploitation \text{U.} Comment doit-elle s'approvisionner auprès des exploitations \text{U} et \text{V}\: ?




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
[D'après Bac S - Polynésie - 2018.]
La municipalité d'une grande ville dispose d'un stock de DVD qu'elle propose en location aux usagers des
différentes médiathèques de cette ville.
Afin de renouveler son offre de location, la municipalité décide de retirer des DVD de son stock.
Parmi les DVD retirés, certains sont défectueux, d'autres non. Parmi les 6 % de DVD défectueux sur l'ensemble du stock, 98 % sont retirés.
On admet par ailleurs que, parmi les DVD non défectueux, 92 % sont maintenus dans le stock et les autres sont retirés.
On choisit un DVD au hasard dans le stock de la municipalité. On considère les événements suivants :
On note \overline \text{D} et \overline \text{R} les événements complémentaires respectifs des événements \text{D} et \text{R.}
Afin de renouveler son offre de location, la municipalité décide de retirer des DVD de son stock.
Parmi les DVD retirés, certains sont défectueux, d'autres non. Parmi les 6 % de DVD défectueux sur l'ensemble du stock, 98 % sont retirés.
On admet par ailleurs que, parmi les DVD non défectueux, 92 % sont maintenus dans le stock et les autres sont retirés.
On choisit un DVD au hasard dans le stock de la municipalité. On considère les événements suivants :
- \text{D} : « le DVD est défectueux » ;
- \text{R} : « le DVD est retiré du stock ».
On note \overline \text{D} et \overline \text{R} les événements complémentaires respectifs des événements \text{D} et \text{R.}
1. Démontrer que la probabilité de l'événement \text{R} est 0\text{,}134.
2. Une association caritative contacte la municipalité dans l'objectif de récupérer l'ensemble des DVD qui sont retirés du stock. Un responsable de la ville affirme alors que, parmi ces DVD retirés, plus de la moitié est composée
de DVD défectueux. Cette affirmation est-elle vraie ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
[D'après Bac S - Amérique du Nord - 2017.]
Dans le cadre de son activité, une entreprise reçoit régulièrement des demandes de devis.
Elle décide d'installer un logiciel anti-spam.
Ce logiciel détecte les messages indésirables appelés spams (messages malveillants, publicités, etc.) et les déplace dans un fichier appelé « dossier spam ».
Le concepteur du logiciel affirme que 95 % des spams sont déplacés. De son côté, l'entrepreneur sait que 60 % des messages qu'il reçoit sont des spams.
Après installation du logiciel, il constate que 58\text{,}6 % des messages sont déplacés dans le dossier spam.
Pour un message pris au hasard, on considère les événements suivants :
Ce logiciel détecte les messages indésirables appelés spams (messages malveillants, publicités, etc.) et les déplace dans un fichier appelé « dossier spam ».
Le concepteur du logiciel affirme que 95 % des spams sont déplacés. De son côté, l'entrepreneur sait que 60 % des messages qu'il reçoit sont des spams.
Après installation du logiciel, il constate que 58\text{,}6 % des messages sont déplacés dans le dossier spam.
Pour un message pris au hasard, on considère les événements suivants :
- \text{D} : « le message est déplacé » ;
- \text{S} : « le message est un spam ».
1. Calculer \text{P} ( \text{S} \cap \text{D} ).
2. On choisit au hasard un message qui n'est pas un spam. Montrer que la probabilité qu'il soit déplacé est égale à 0\text{,}04.
3. On choisit au hasard un message non déplacé. Quelle est la probabilité que ce message soit un spam ?
2. On choisit au hasard un message qui n'est pas un spam. Montrer que la probabilité qu'il soit déplacé est égale à 0\text{,}04.
3. On choisit au hasard un message non déplacé. Quelle est la probabilité que ce message soit un spam ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
[D'après Bac S - France métropolitaine - 2013.]


Une jardinerie vend de jeunes plants d'arbres qui
proviennent de trois horticulteurs : 35 % des plants
proviennent de l'horticulteur \text{H}_1, 25 % de l'horticulteur
\text{H}_2 et le reste de l'horticulteur \text{H}_3.
Chaque horticulteur livre deux catégories d'arbres : des conifères et des arbres à feuilles. La livraison de l'horticulteur \text{H}_1 comporte 80 % de conifères alors que celle de l'horticulteur \text{H}_2 n'en comporte que 50 % et celle de l'horticulteur \text{H}_3 seulement 30 %.
Chaque horticulteur livre deux catégories d'arbres : des conifères et des arbres à feuilles. La livraison de l'horticulteur \text{H}_1 comporte 80 % de conifères alors que celle de l'horticulteur \text{H}_2 n'en comporte que 50 % et celle de l'horticulteur \text{H}_3 seulement 30 %.
1. Le gérant de la jardinerie choisit un arbre au hasard
dans son stock. On envisage les événements suivants :
a. Construire un arbre pondéré traduisant la situation.
- \text{H}_1 : « l'arbre choisi a été acheté chez l'horticulteur \text{H}_1 » ;
- \text{H}_2 : « l'arbre choisi a été acheté chez l'horticulteur \text{H}_2 » ;
- \text{H}_3 : « l'arbre choisi a été acheté chez l'horticulteur \text{H}_3 » ;
- \text{C} : « l'arbre choisi est un conifère » ;
- \text{F} : « l'arbre choisi est un arbre feuillu ».
a. Construire un arbre pondéré traduisant la situation.
Cliquez pour accéder à une zone de dessin
b. Calculer la probabilité que l'arbre choisi soit un
conifère acheté chez l'horticulteur \text{H}_3.
c. Justifier que la probabilité de l'événement \text{C} est égale à 0\text{,}525.
d. L'arbre choisi est un conifère. Quelle est la probabilité qu'il ait été acheté chez l'horticulteur \text{H}_1\:? On arrondira à 10^{-3} près.
c. Justifier que la probabilité de l'événement \text{C} est égale à 0\text{,}525.
d. L'arbre choisi est un conifère. Quelle est la probabilité qu'il ait été acheté chez l'horticulteur \text{H}_1\:? On arrondira à 10^{-3} près.
2. On choisit au hasard deux arbres dans le stock de
cette jardinerie. On suppose que ce stock est suffisamment important pour que ce choix puisse être assimilé à un tirage avec remise de deux arbres dans le stock. On appelle \text{X} la variable aléatoire qui donne le nombre de conifères choisis.
a. Calculer et interpréter \text{P}(\text{X} = 0).
b. En déduire \text{P}(\text{X}\geqslant 1 ) puis interpréter le résultat.
a. Calculer et interpréter \text{P}(\text{X} = 0).
b. En déduire \text{P}(\text{X}\geqslant 1 ) puis interpréter le résultat.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
[D'après Bac S - France métropolitaine - 2018.]
Le virus de la grippe atteint chaque année, en période hivernale, une partie de la population d'une ville. La vaccination contre la grippe est possible mais elle doit être renouvelée chaque année. L'efficacité du vaccin contre la grippe peut être diminuée en fonction des caractéristiques individuelles des personnes vaccinées ou en raison du vaccin, qui n'est pas toujours totalement adapté aux souches du virus qui circulent. Il est donc possible de contracter la grippe tout en étant vacciné.
Une étude menée dans la population de la ville à l'issue de la période hivernale a permis de constater que :
On choisit une personne au hasard dans la population de la ville et on considère les événements :
Une étude menée dans la population de la ville à l'issue de la période hivernale a permis de constater que :
- 40 % de la population est vaccinée ;
- 8 % des personnes vaccinées ont contracté la grippe ;
- 20 % de la population a contracté la grippe.
On choisit une personne au hasard dans la population de la ville et on considère les événements :
- \text{V} : « la personne est vaccinée contre la grippe » ;
- \text{G} : « la personne a contracté la grippe ».
1. a. Donner la probabilité de l'événement \text{G.}
b. Dans l'arbre pondéré ci-dessous, compléter les pointillés indiqués sur quatre de ses branches.

b. Dans l'arbre pondéré ci-dessous, compléter les pointillés indiqués sur quatre de ses branches.

1
4
2
3
2. Déterminer la probabilité que la personne choisie ait contracté la grippe et soit vaccinée.
3. La personne choisie n'est pas vaccinée. Montrer que la probabilité qu'elle ait contracté la grippe est égale à 0\text{,}28.
3. La personne choisie n'est pas vaccinée. Montrer que la probabilité qu'elle ait contracté la grippe est égale à 0\text{,}28.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
[D'après Bac S - Amérique du Sud - 2015.]
Le chikungunya est une maladie virale transmise d'un être humain à l'autre par les piq�ûres de moustiques
femelles infectées. Un test a été mis au point pour le dépistage de ce virus. Le laboratoire fabriquant ce test
fournit les caractéristiques suivantes :
On procède à un test de dépistage systématique dans une population « cible ». Un individu est choisi au hasard dans cette population. On appelle :
On notera \overline { \mathrm {M} } l'événement complémentaire de l'événement \text{M.} On notera \overline { \mathrm {T} } l'événement complémentaire de l'événement \text{T.} On note p ( 0 \leqslant p \leqslant 1 ) la proportion de personnes atteintes par la maladie dans la population cible.
- la probabilité qu'une personne atteinte par le virus ait un test positif est de 0\text{,}98\: ;
- la probabilité qu'une personne non atteinte par le virus ait un test positif est de 0\text{,}01.
On procède à un test de dépistage systématique dans une population « cible ». Un individu est choisi au hasard dans cette population. On appelle :
- \text{M} l'événement : « l'individu choisi est atteint du chikungunya » ;
- \text{T} l'événement : « le test de l'individu choisi est positif ».
On notera \overline { \mathrm {M} } l'événement complémentaire de l'événement \text{M.} On notera \overline { \mathrm {T} } l'événement complémentaire de l'événement \text{T.} On note p ( 0 \leqslant p \leqslant 1 ) la proportion de personnes atteintes par la maladie dans la population cible.
1. a. Compléter l'arbre de probabilité ci-dessous.

b. Exprimer \mathrm { P } ( \mathrm { M } \cap \mathrm { T } ), \mathrm { P } ( \overline { \mathrm { M } } \cap \mathrm { T } ) puis \mathrm { P } ( \mathrm { T } ) en fonction de p .

1
2
3
4
5
6
b. Exprimer \mathrm { P } ( \mathrm { M } \cap \mathrm { T } ), \mathrm { P } ( \overline { \mathrm { M } } \cap \mathrm { T } ) puis \mathrm { P } ( \mathrm { T } ) en fonction de p .
2. a. Démontrer que la probabilité de réaliser \text{M} sachant que \text{T} est réalisé est donnée par la fonction f
définie sur [ 0\: ; 1 ] par : f(p) = \dfrac { 98 p } { 97 p + 1 }.
b. Étudier et interpréter les variations de la fonction f .
b. Étudier et interpréter les variations de la fonction f .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8
[D'après Bac S - France métropolitaine - 2017.]
On étudie un modèle de propagation d'un virus dans une population, semaine après semaine.
Chaque individu de la population peut être, à l'exclusion de toute autre possibilité :
Un individu est immunisé lorsqu'il a été vacciné, ou lorsqu'il a guéri après avoir été atteint par le virus. Pour tout entier naturel n , le modèle de propagation du virus est défini par les règles suivantes :
On choisit au hasard un individu dans la population. On considère les événements suivants :
En semaine 0, tous les individus sont considérés « de type S », on a donc les probabilités suivantes : \text{P} \left( \text{S} _ { 0 } \right) = 1 \:; \text{P} \left( \text{M} _ { 0 } \right) = 0 et \text{P} \left( \text{I} _ { 0 } \right) = 0.
- soit susceptible d'être atteint par le virus, on dira qu'il est « de type S » ;
- soit malade (atteint par le virus) ;
- soit immunisé (ne peut plus être atteint par le virus).
Un individu est immunisé lorsqu'il a été vacciné, ou lorsqu'il a guéri après avoir été atteint par le virus. Pour tout entier naturel n , le modèle de propagation du virus est défini par les règles suivantes :
- parmi les individus de type S en semaine n , on observe qu'en semaine n + 1 : 85 % restent de type S, 5 % deviennent malades et 10 % deviennent immunisés ;
- parmi les individus malades en semaine n , on observe qu'en semaine n + 1 : 65 % restent malades, et 35 % sont guéris et deviennent immunisés ;
- tout individu immunisé en semaine n reste immunisé en semaine n + 1 .
On choisit au hasard un individu dans la population. On considère les événements suivants :
- \text{S}_n : « l'individu est de type S en semaine n » ;
- \text{M}_n : « l'individu est malade en semaine n » ;
- \text{I}_n : « l'individu est immunisé en semaine n ».
En semaine 0, tous les individus sont considérés « de type S », on a donc les probabilités suivantes : \text{P} \left( \text{S} _ { 0 } \right) = 1 \:; \text{P} \left( \text{M} _ { 0 } \right) = 0 et \text{P} \left( \text{I} _ { 0 } \right) = 0.
Partie A :
On étudie l'évolution de l'épidémie au cours des semaines 1 et 2.
1. Compléter l'arbre de probabilité donné ci-dessous :

2. Montrer que \text{P} \left( \text{I} _ { 2 } \right) = 0\text{,}202\:5 .
3. Sachant qu'un individu est immunisé en semaine 2, quelle est la probabilité, arrondie au millième, qu'il ait été malade en semaine 1 ?
Partie B :
On étudie à long terme l'évolution de la maladie. Pour tout entier naturel n , on : u _ { n } = \mathrm {P} \left(\mathrm {S}_ { n } \right), v _ { n } = \mathrm {P} \left(\mathrm {M}_ { n } \right) et w _ { n } = \mathrm {P} \left(\mathrm {I}_ { n } \right) les probabilités respectives des événements \text{S}_n , \text{M}_n et \text{I}_n .
1. Justifier que, pour tout entier naturel n , on a : u _ { n } + v _ { n } + w _ { n } = 1. On admet que la suite \left( v _ { n } \right) est définie par v _ { n + 1 } = 0\text{,}65 v _ { n } + 0\text{,}05 u _ { n }.
2. À l'aide d'un tableur, on a calculé les premiers termes des suites \left( u _ { n } \right), \left( v _ { n } \right) et \left( w _ { n } \right).
On étudie l'évolution de l'épidémie au cours des semaines 1 et 2.
1. Compléter l'arbre de probabilité donné ci-dessous :

1
2
3
4
5
6
7
8
9
10
11
12
13
14
2. Montrer que \text{P} \left( \text{I} _ { 2 } \right) = 0\text{,}202\:5 .
3. Sachant qu'un individu est immunisé en semaine 2, quelle est la probabilité, arrondie au millième, qu'il ait été malade en semaine 1 ?
Partie B :
On étudie à long terme l'évolution de la maladie. Pour tout entier naturel n , on : u _ { n } = \mathrm {P} \left(\mathrm {S}_ { n } \right), v _ { n } = \mathrm {P} \left(\mathrm {M}_ { n } \right) et w _ { n } = \mathrm {P} \left(\mathrm {I}_ { n } \right) les probabilités respectives des événements \text{S}_n , \text{M}_n et \text{I}_n .
1. Justifier que, pour tout entier naturel n , on a : u _ { n } + v _ { n } + w _ { n } = 1. On admet que la suite \left( v _ { n } \right) est définie par v _ { n + 1 } = 0\text{,}65 v _ { n } + 0\text{,}05 u _ { n }.
2. À l'aide d'un tableur, on a calculé les premiers termes des suites \left( u _ { n } \right), \left( v _ { n } \right) et \left( w _ { n } \right).

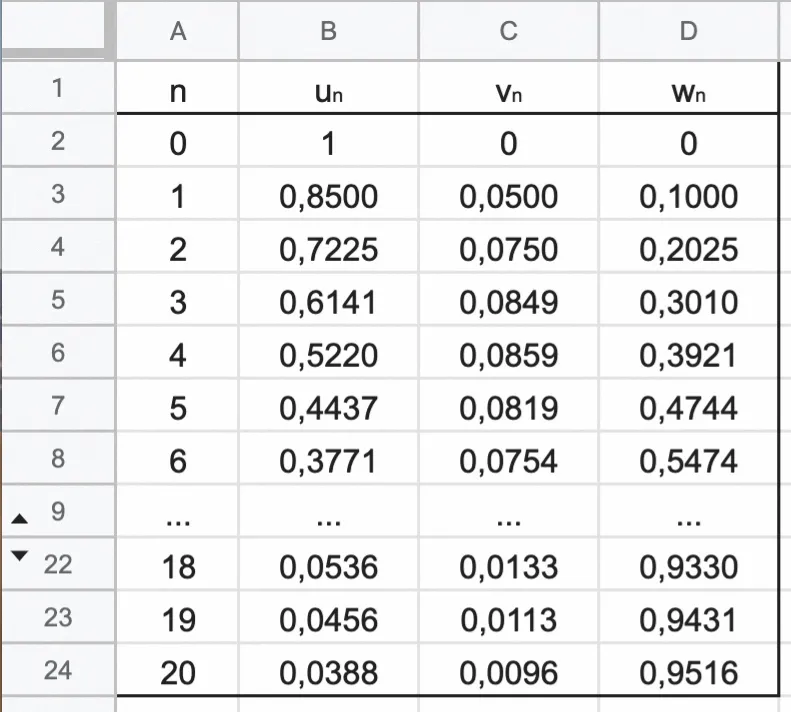
Pour répondre aux questions a. et b. suivantes, on utilisera la feuille de calcul reproduite ci-dessus.
a. Quelle formule, saisie dans la cellule C3, permet par recopie vers le bas, de calculer les termes de la suite \left( v _ { n } \right) \: ?
b. On admet que les termes de \left( v _ { n } \right) augmentent, puis diminuent à partir d'un certain rang \text{N,} appelé le « pic épidémique » : c'est l'indice de la semaine pendant laquelle la probabilité d'être malade pour un individu choisi au hasard est la plus grande. Déterminer la valeur du pic épidémique prévue par ce modèle.
3. Justifier que, pour tout entier naturel n , on a : u _ { n + 1 } = 0\text{,}85 u _ { n }. En déduire l'expression de u_n en fonction de n .
4. On admet que v _ { n } = \dfrac { 1 } { 4 } \left( 0\text{,}85 ^ { n } - 0\text{,}65 ^ { n } \right). À l'aide d'une représentation graphique des suites \left( u _ { n } \right), \left( v _ { n } \right) et \left( w _ { n } \right), que peut-on en déduire quant à l'évolution de l'épidémie prévue à long terme par ce modèle ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9
[D'après Bac S - La Réunion - 2010.]
Dans cet exercice, tous les résultats seront donnés sous forme de fractions irréductibles.
Partie A :
On dispose d'un dé cubique \text{A} parfaitement équilibré possédant une face verte, deux faces noires et trois faces rouges.
Un jeu consiste à lancer deux fois de suite et de manière indépendante ce dé. On note à chaque lancer la couleur de la face obtenue.
1. Calculer la probabilité pour qu'à l'issue d'un jeu, les deux faces obtenues soient noires.
2. Soit l'événement \text{C} : « à l'issue d'un jeu, les deux faces obtenues sont de la même couleur ». Démontrer que la probabilité de l'événement \text{C} est égale à \dfrac { 7 } { 18 }.
3. Calculer la probabilité pour qu'à l'issue d'un jeu, les deux faces obtenues soient de couleurs différentes.
4. À l'issue d'un jeu, sachant que les deux faces obtenues sont de la même couleur, quelle est la probabilité pour que les deux faces obtenues soient vertes ?
Partie B :
On dispose d'un second dé cubique \text{B} équilibré présentant quatre faces vertes et deux faces noires. Le nouveau jeu se déroule de la manière suivante : on lance le dé \text{B} ,
On dispose d'un dé cubique \text{A} parfaitement équilibré possédant une face verte, deux faces noires et trois faces rouges.
Un jeu consiste à lancer deux fois de suite et de manière indépendante ce dé. On note à chaque lancer la couleur de la face obtenue.
1. Calculer la probabilité pour qu'à l'issue d'un jeu, les deux faces obtenues soient noires.
2. Soit l'événement \text{C} : « à l'issue d'un jeu, les deux faces obtenues sont de la même couleur ». Démontrer que la probabilité de l'événement \text{C} est égale à \dfrac { 7 } { 18 }.
3. Calculer la probabilité pour qu'à l'issue d'un jeu, les deux faces obtenues soient de couleurs différentes.
4. À l'issue d'un jeu, sachant que les deux faces obtenues sont de la même couleur, quelle est la probabilité pour que les deux faces obtenues soient vertes ?
Partie B :
On dispose d'un second dé cubique \text{B} équilibré présentant quatre faces vertes et deux faces noires. Le nouveau jeu se déroule de la manière suivante : on lance le dé \text{B} ,
- si la face obtenue est verte, on lance à nouveau le dé \text{B} et on note la couleur de la face obtenue ;
- si la face obtenue est noire, on lance le dé \text{A} et on note la couleur de la face obtenue.
1. a. Construire un arbre de probabilité traduisant cette situation.
b. Quelle est la probabilité d'obtenir une face verte au deuxième lancer, sachant que l'on a obtenu une face verte au premier lancer ?
2. Montrer que la probabilité d'obtenir deux faces vertes est égale à \dfrac { 4 } { 9 }.
3. Quelle est la probabilité d'obtenir une face verte au deuxième lancer ?
Cliquez pour accéder à une zone de dessin
b. Quelle est la probabilité d'obtenir une face verte au deuxième lancer, sachant que l'on a obtenu une face verte au premier lancer ?
2. Montrer que la probabilité d'obtenir deux faces vertes est égale à \dfrac { 4 } { 9 }.
3. Quelle est la probabilité d'obtenir une face verte au deuxième lancer ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

