Mathématiques 1re Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 8
TP / TICE 2
Approcher le cosinus d'un nombre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
On admet la formule suivante pour tout réel x proche de 0 :
Questions préliminaires :
Soit n un entier naturel. On appelle factorielle de n le nombre, noté n!, défini par n !=n \times(n-1) \times(n-2) \times \ldots \times 1. Par convention, 0! = 1 .
1. Calculer 1! , 3! et 7! .
2. Écrire la formule de \cos(x) donnée dans l'énoncé à l'aide de la notation factorielle.
3. Déterminer les deux termes suivants dans la formule, c'est-à-dire celui avec x^8 et celui avec x^{10}.
\cos (x)=1-\dfrac{x^{2}}{2 \times 1}+\dfrac{x^{4}}{4 \times 3 \times 2 \times 1}-\dfrac{x^{6}}{6 \times 5 \times 4 \times 3 \times 2 \times 1}+\ldots
Remarque
Cette formule s'appelle le développement limité en 0 du cosinus.Questions préliminaires :
Soit n un entier naturel. On appelle factorielle de n le nombre, noté n!, défini par n !=n \times(n-1) \times(n-2) \times \ldots \times 1. Par convention, 0! = 1 .
1. Calculer 1! , 3! et 7! .
2. Écrire la formule de \cos(x) donnée dans l'énoncé à l'aide de la notation factorielle.
3. Déterminer les deux termes suivants dans la formule, c'est-à-dire celui avec x^8 et celui avec x^{10}.
4. Justifier que, pour tout entier naturel n \neq 0 , n !=n \times(n-1) !.
5. On a réalisé un programme avec Python qui permet de calculer n!. Pour cela, on a créé une fonction \bf{Factorielle}. Expliquer le programme.
5. On a réalisé un programme avec Python qui permet de calculer n!. Pour cela, on a créé une fonction \bf{Factorielle}. Expliquer le programme.
def Factorielle(n):
if n == 0:
return(1)
else:
return(n * Factorielle(n - 1))
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Approcher le cosinus d'un nombre proche de 0 simplement à l'aide des quatre opérations élémentaires en utilisant une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1GeoGebra
1. Ouvrir GeoGebra en mode graphique et tracer la
courbe représentative de f : x \mapsto \cos (x).
GeoGebra
2. a. Tracer la courbe représentative de f_{1} : x \mapsto 1-\dfrac{x^{2}}{2 \times 1}.
b. Tracer la courbe représentative de f_{2} : x \mapsto 1-\dfrac{x^{2}}{2 \times 1}+\dfrac{x^{4}}{4 \times 3 \times 2 \times 1}.
c. Tracer la courbe représentative de f_{3} : x \mapsto 1-\dfrac{x^{2}}{2 \times 1}+\dfrac{x^{4}}{4 \times 3 \times 2 \times 1}-\dfrac{x^{6}}{6 \times 5 \times 4 \times 3 \times 2 \times 1}.
d. Que remarque-t-on ?
3. Créer un curseur n variant de 1 à 10 avec un pas de 1.
4. Le but à présent est de tracer la fonction x \mapsto 1-\dfrac{x^{2}}{2 \times 1}+\dfrac{x^{4}}{4 \times 3 \times 2 \times 1}-\ldots+(-1)^{n} \dfrac{x^{2 n}}{(2 n) !} pour différentes valeurs de n . Pour cela, rentrer dans la zone de saisie :
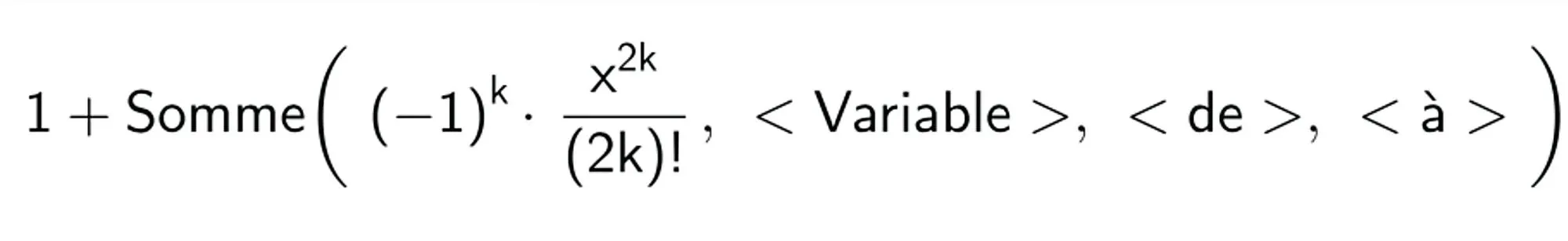puis compléter cette commande de manière adéquate.
5. Faire varier n . Que remarque-t-on ?
b. Tracer la courbe représentative de f_{2} : x \mapsto 1-\dfrac{x^{2}}{2 \times 1}+\dfrac{x^{4}}{4 \times 3 \times 2 \times 1}.
c. Tracer la courbe représentative de f_{3} : x \mapsto 1-\dfrac{x^{2}}{2 \times 1}+\dfrac{x^{4}}{4 \times 3 \times 2 \times 1}-\dfrac{x^{6}}{6 \times 5 \times 4 \times 3 \times 2 \times 1}.
d. Que remarque-t-on ?
3. Créer un curseur n variant de 1 à 10 avec un pas de 1.
4. Le but à présent est de tracer la fonction x \mapsto 1-\dfrac{x^{2}}{2 \times 1}+\dfrac{x^{4}}{4 \times 3 \times 2 \times 1}-\ldots+(-1)^{n} \dfrac{x^{2 n}}{(2 n) !} pour différentes valeurs de n . Pour cela, rentrer dans la zone de saisie :
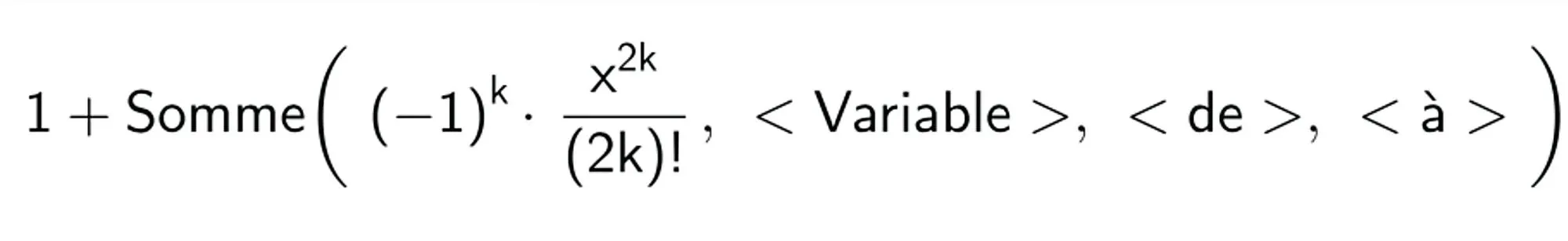
5. Faire varier n . Que remarque-t-on ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Python
Le but est d'effectuer un programme permettant de calculer la valeur approchée du cosinus d'un réel x en utilisant la formule de l'énoncé. Pour cela, on fournit un algorithme à compléter.
1. Expliquer le rôle des variables \bf{denom} et \bf{sign} ainsi que le rôle des lignes 6 et 7.
2. Recopier et compléter la ligne 8.
3. Programmer cet algorithme sur Python.
4. Le tester pour différentes valeurs de x et de n .
5. Lorsque x est choisi proche de 0 et que n devient de plus en plus grand, de quelle valeur s'approche le résultat calculé par le programme ? Est-ce surprenant ?
\boxed{
\begin{array} { l } {1 \:\:\: \text {Fonction : cos}\_ \text {approx (x, n)} } \\
2 \quad\:\: \text {res} \leftarrow 1 \\
3\quad \:\:\text {denom} \leftarrow 1 \\
4\quad \:\:\text {sign} \leftarrow 1 \\
5\quad \:\:\text {Pour k allant de 1 à n + 1 :} \\
6\quad \:\:\quad \text {denom} \leftarrow \text{factorielle(2} \times \text{k}) \\
7\quad \:\:\quad \text {sign} \leftarrow \text {sign} \times (-1) \\
8\quad \:\:\quad \text {res} \leftarrow \text {...} \\
9\quad \:\:\text {Fin Pour} \\
10\quad \text {Retourner res} \\
\end{array}
}
1. Expliquer le rôle des variables \bf{denom} et \bf{sign} ainsi que le rôle des lignes 6 et 7.
2. Recopier et compléter la ligne 8.
3. Programmer cet algorithme sur Python.
Cliquez pour accéder à la correction
4. Le tester pour différentes valeurs de x et de n .
Cliquez pour accéder à la correction
5. Lorsque x est choisi proche de 0 et que n devient de plus en plus grand, de quelle valeur s'approche le résultat calculé par le programme ? Est-ce surprenant ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
