Les parties de cet exercice sont indépendantes et chacune d'entre elles peut être réalisée seul(e) ou en groupe. Les élèves mettent leurs résultats en commun pour résoudre le problème.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Énoncé

Le but de ce problème est de découvrir et d'étudier la fonction tangente.
La fonction tangente est définie par l'expression \tan (x)=\dfrac{\sin (x)}{\cos (x)} sur un ensemble \mathcal{D} qui sera déterminé par la suite.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Partie 1

Dans cette partie, on va montrer que l'expression fournie correspond bien à la tangente vue au collège.

1. Proposer un schéma et rappeler les formules du cosinus, du sinus et de la tangente d'un angle aigu dans un triangle rectangle.

Cliquez pour accéder à une zone de dessin

Cette fonctionnalité est accessible dans la version Premium.

2. Vérifier que la tangente correspond bien au quotient du sinus par le cosinus.

3. Avec la formule de l'énoncé, que vaut la tangente en \dfrac{\pi}{4} ? Et en -\dfrac{\pi}{4} ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Partie 2

Dans cette partie, on va conjecturer des propriétés sur la fonction tangente à l'aide de la calculatrice puis les démontrer.

1. Tracer sur la calculatrice le graphe de la fonction tangente sur l'intervalle [-2 \pi \:; 2 \pi] puis répondre aux questions suivantes.

a. L'ensemble de définition semble-t-il être \mathbb{R} tout entier ?

b. La fonction semble-t-elle paire ? Impaire ?

c. La fonction semble-t-elle périodique ? Si oui, quelle est sa période ?

2. Démontrer les réponses des questions précédentes.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Partie 3

Dans cette partie, on va étudier la dérivabilité de la fonction tangente.

1. Pour quelles valeurs ne peut-on ni calculer, ni dériver la fonction \tan : x \mapsto \dfrac{\sin (x)}{\cos (x)} ?

2. Donner une expression de la dérivée de la fonction tangente (on pourra l'exprimer en fonction de \tan(x)).

3. En déduire les variations de la fonction tangente.

4. Proposer un tableau de variations sur [-\pi \:; \pi].

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Partie 4

Dans cette partie, on va retrouver la valeur de la tangente par lecture graphique sur le cercle trigonométrique.

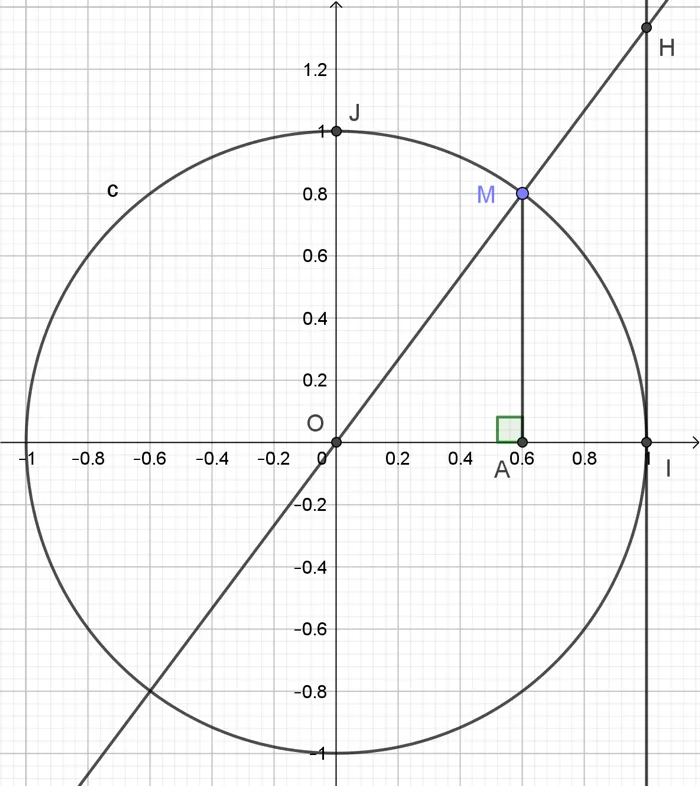
1. Reproduire un cercle trigonométrique dans un repère (\mathrm{O} ; \mathrm{I}, \mathrm{J}) et placer un point \text{M}, point image d'un réel x compris entre \dfrac{\pi}{4} et \dfrac{\pi}{3}. Tracer la tangente d du cercle en \text{I}. La droite \text{(OM)} coupe d en \text{H}.

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

2. À l'aide du théorème de Thalès, montrer que la longueur \text{IH} est égale à la tangente de l'angle ainsi créé.

3. Que se passe-t-il en \dfrac{\pi}{2} ?

Cliquez ici pour avoir accès à une correction

Le zoom est accessible dans la version Premium.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Mise en commun

À l'aide des différents résultats, proposer une étude complète de la fonction tangente. Proposer également une explication de ce qu'il se passe en \dfrac{\pi}{2}.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Pour aller plus loin

Le plan est muni d'un repère orthonormé (\mathrm{O} ; \mathrm{I}, \mathrm{J}). Sur le cercle trigonométrique, on place un point \text{A} tel que x_{\mathrm{A}} \neq 0 et y_{\mathrm{A}} \neq 0. On trace la perpendiculaire à (\text{OA}) passant par \text{A} : elle coupe l'axe des abscisses en \text{C} et l'axe des ordonnées en \text{B.} Démontrer, en utilisant la tangente de l'angle \widehat{\mathrm{IOA}} que \mathrm{AC}=\dfrac{1}{\mathrm{AB}}.

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

Oups, une coquille

j'ai une idée !

Nous préparons votre pageNous vous offrons 5 essais

Yolène

Émilie

Jean-Paul

Fatima

Sarah

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.