Chapitre 7
TP Info 1
Algorithme de Ehrenfest
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
On considère deux urnes \mathrm{A} et \mathrm{B} et un entier \mathrm{N} \geqslant 1. Dans l'urne \mathrm{A} se trouvent \mathrm{N} boules numérotées de 0 à \mathrm{N}-1.
On répète n fois les actions suivantes :
On répète n fois les actions suivantes :
- choisir au hasard un nombre entre 0 et \mathrm{N}-1 ;
- placer la boule ayant ce numéro dans l'urne où elle n'est pas.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Simuler l'évolution du nombre de boules dans chaque urne après un grand nombre de tirages à l'aide d'une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Tableur
La zone en vert indique la boule que l'on change d'urne à l'étape considérée. Dans les lignes 3 à 14, un 1 indique que la boule se trouve dans l'urne A et un 0 indique que la boule se trouve dans l'urne B. Au départ (Étape 0), toutes les boules sont dans l'urne A.

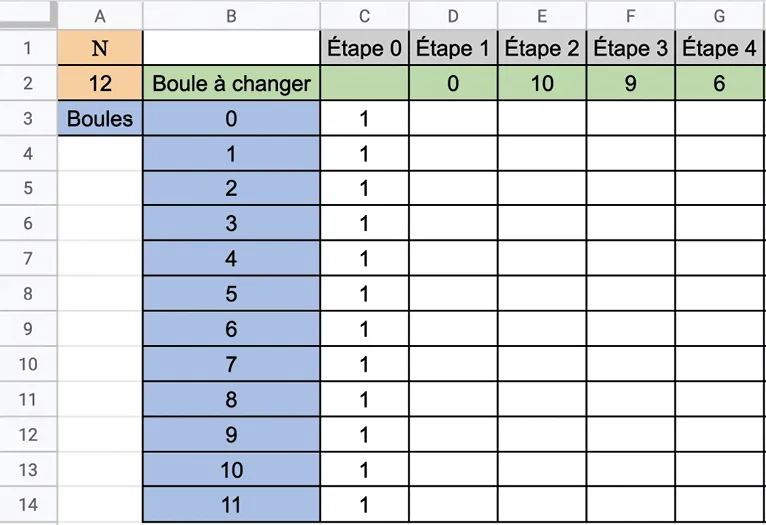
1. Recopier cette feuille de calcul (sauf les nombres dans la zone verte) et écrire dans la cellule D2 une formule permettant de choisir au hasard un nombre entier compris entre 0 et \mathrm{N}-1 où \mathrm{N} désigne le nombre situé en A2.
Étirer ensuite cette formule vers la droite.
2. Quelle formule doit‑on écrire dans les cellules D3 à D14 pour que la boule considérée change d'urne si, et seulement si, son numéro est celui qui se trouve en D2 ? Étirer ensuite cette formule vers la droite afin de modéliser l'évolution de la position des boules pour 100 étapes.
3. Calculer dans la ligne 15 la proportion de 1 (donc de boules se trouvant dans l'urne A) à chaque étape.
Étirer ensuite cette formule vers la droite.
2. Quelle formule doit‑on écrire dans les cellules D3 à D14 pour que la boule considérée change d'urne si, et seulement si, son numéro est celui qui se trouve en D2 ? Étirer ensuite cette formule vers la droite afin de modéliser l'évolution de la position des boules pour 100 étapes.
3. Calculer dans la ligne 15 la proportion de 1 (donc de boules se trouvant dans l'urne A) à chaque étape.
4. Vers quelle valeur cette proportion semble‑t‑elle converger ?
5. Tester cette hypothèse en augmentant le nombre d'étapes simulées.
5. Tester cette hypothèse en augmentant le nombre d'étapes simulées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Python
1. Que modélise la variable Boules ?
2. Compléter les lignes 13, 15 et 17 du programme ci-après.
3. Utiliser le programme pour déterminer, au bout de 1 000 tirages, la proportion de boules dans chaque urne.
2. Compléter les lignes 13, 15 et 17 du programme ci-après.
3. Utiliser le programme pour déterminer, au bout de 1 000 tirages, la proportion de boules dans chaque urne.
from random import* N = 20 #Nombre de boules. n = 1000 #Nombre de tirages. #Les boules sont toutes dans l'urne A au départ. Boules = [] for j in range(N): Boules.append() #Choisir une boule et la changer d'urne. for i in range(n): numero = ... if Boules[numero] == 1: Boules[numero] = ... else: Boules[numero] = ... #Compter la proportion de boules dans l'urne A compteur = 0 for k in Boules: compteur = compteur + k proportion = float(compteur/N) print(proportion)
4. Recommencer plusieurs fois cette simulation et comparer les résultats obtenus.
5. Reprendre les questions précédentes avec différentes valeurs de \mathrm{N} et de n.
5. Reprendre les questions précédentes avec différentes valeurs de \mathrm{N} et de n.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Voir exercice .
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

