Mathématiques Cycle 4

Rejoignez la communauté !

Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.

Thème 1 : Nombres et calculs

Ch. 1

Arithmétique

Ch. 2

Nombres relatifs

Ch. 3

Nombres fractionnaires

Ch. 4

Calcul littéral

Ch. 5

Équations et inéquations

Ch. 6

Proportionnalité

Ch. 7

Puissances

Thème 2 : Organisation et gestion de données

Ch. 8

Statistiques

Ch. 9

Probabilités

Ch. 10

Fonctions

Thème 3 : Grandeurs et mesures

Ch. 11

Grandeurs et mesures

Thème 4 : Espace et géométrie

Ch. 12

Transformations dans le plan

Ch. 13

Triangles

Ch. 14

Angles et droites parallèles

Ch. 15

Géometrie dans l'espace

Ch. 16

Théorème de pythagore

Ch. 17

Agrandissements - réductions

Ch. 18

Trigonométrie

Annexes

Livret algorithmique et programmation

Pistes EPI

Dossier brevet

Chapitre 2

Exercices

Je résous des problèmes

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

53
Vrai ou faux ?

✔ J'utilise des cas particuliers pour orienter ma démarche de résolution.

Justifiez et donnez un exemple si lʼaffirmation est vraie. Il est possible de...

1. trouver deux nombres négatifs tels que leur somme soit positive.

2. trouver deux nombres inférieurs à 10 tels que leur différence soit égale à 20.

3. trouver deux nombres compris entre -10 et 10 dont la somme est égale à -5.

4. trouver deux nombres négatifs tels que leur différence soit négative.

5. trouver deux nombres tels que leur somme soit égale à leur différence.

6. trouver un nombre égal à son opposé.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

54
Savoir refaire
À chacun sa méthode

✔ J'exerce mon esprit critique pour vérifier la cohérence des résultats.

Le zoom est accessible dans la version Premium.

Le zoom est accessible dans la version Premium.

Le zoom est accessible dans la version Premium.

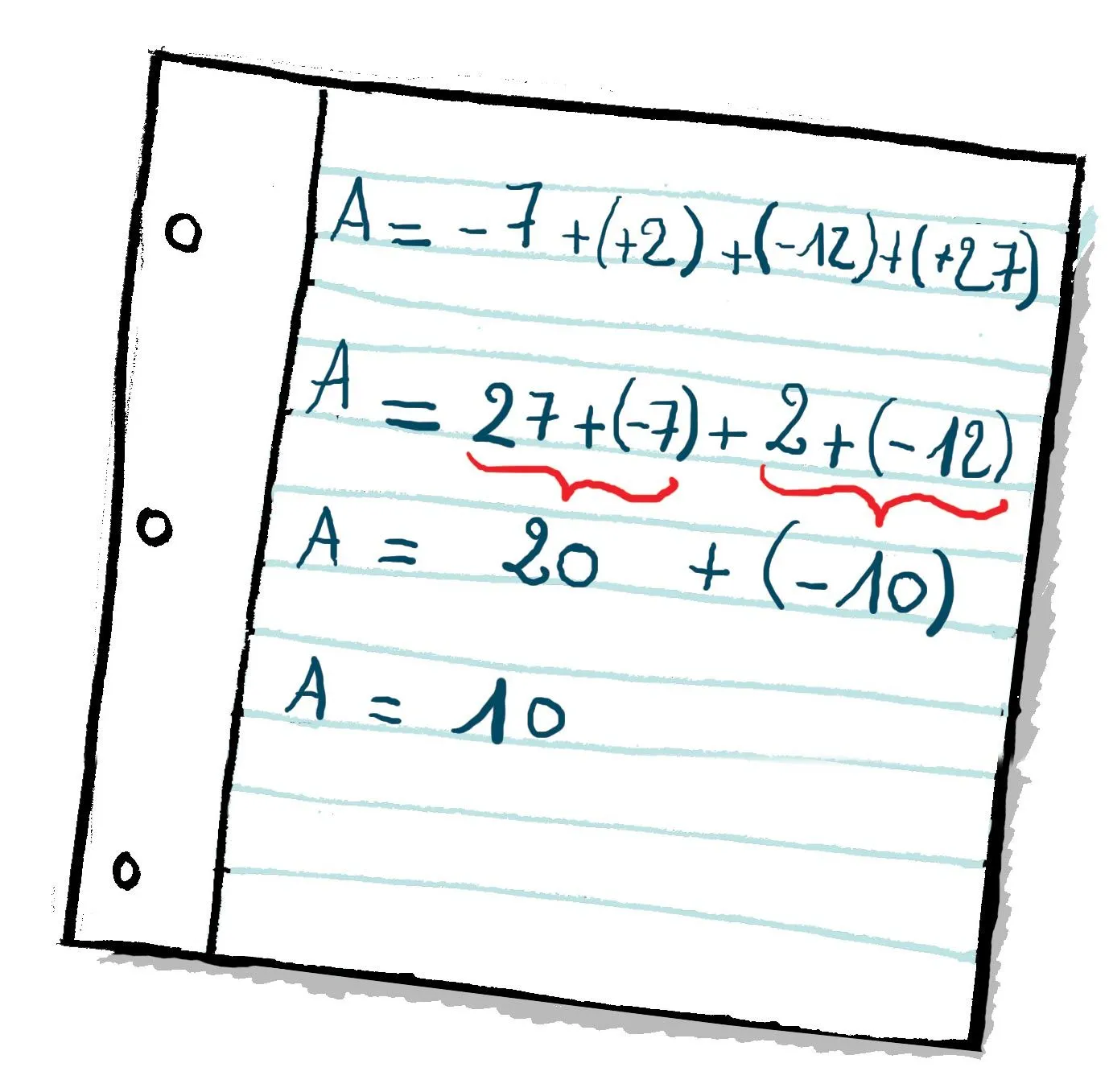
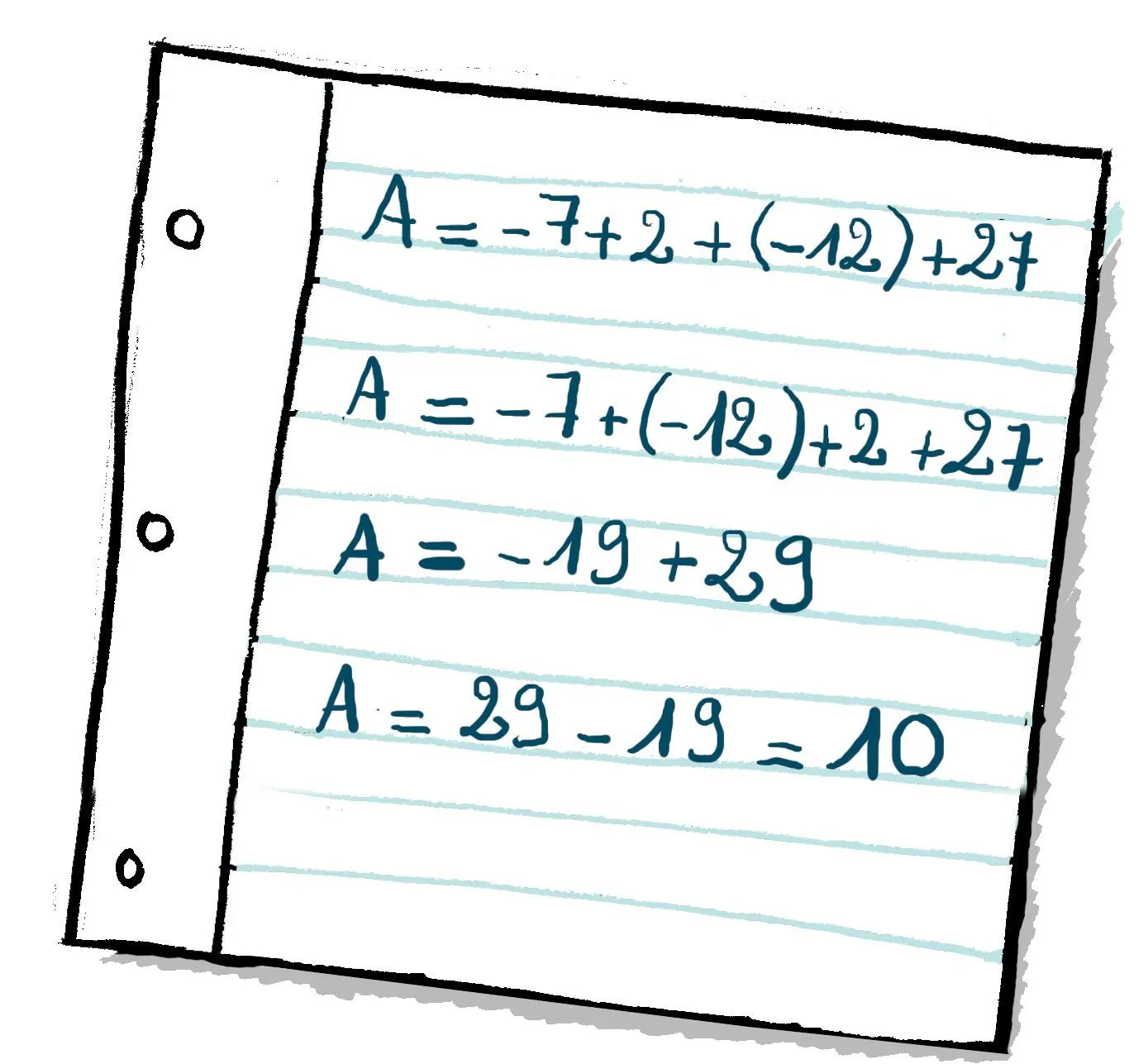Anne, Flore et Arthur doivent calculer l'expression :

A = (- 7) - (- 2) - (+ 12) - (- 27)

. Voici leurs copies.

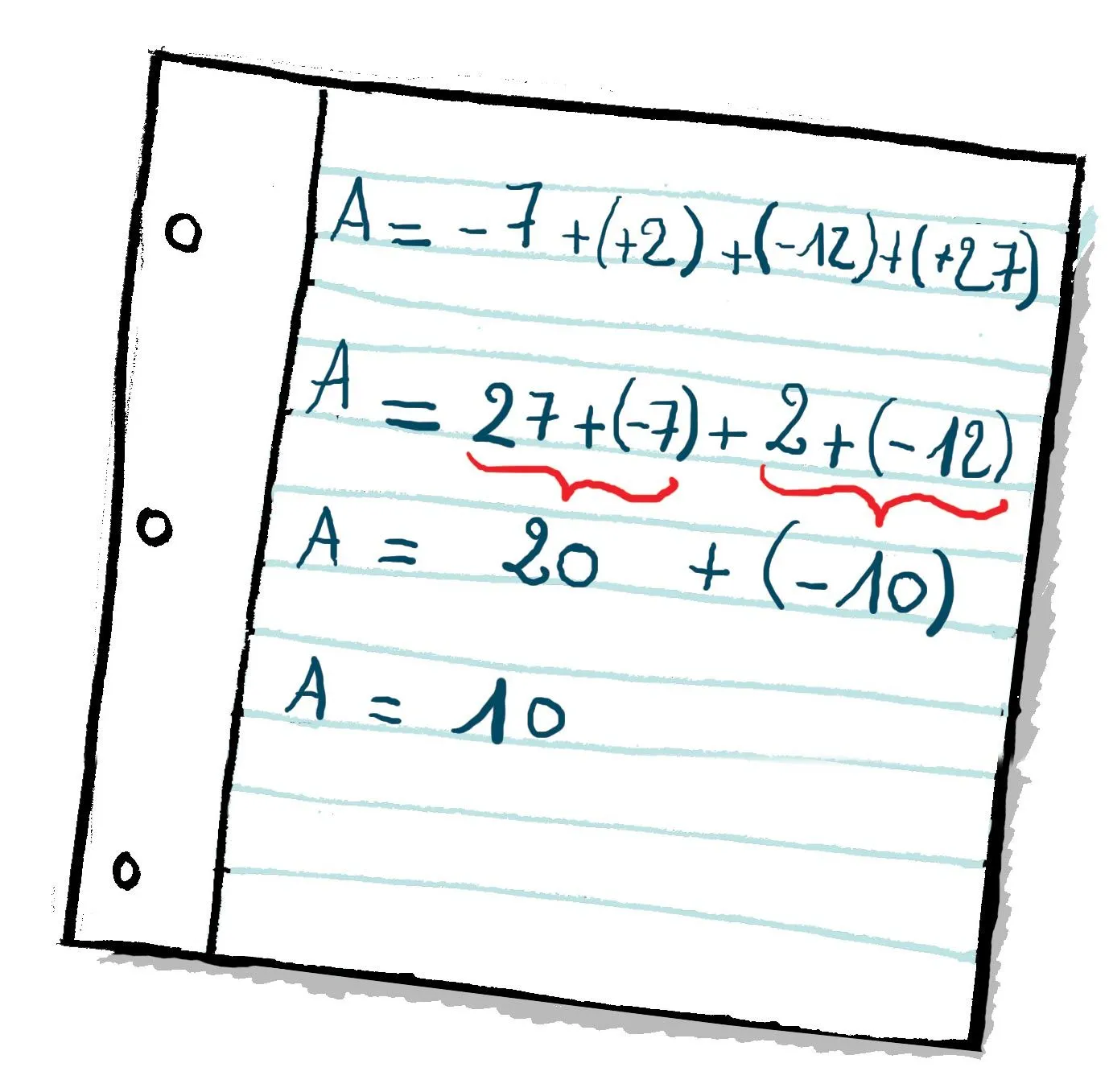
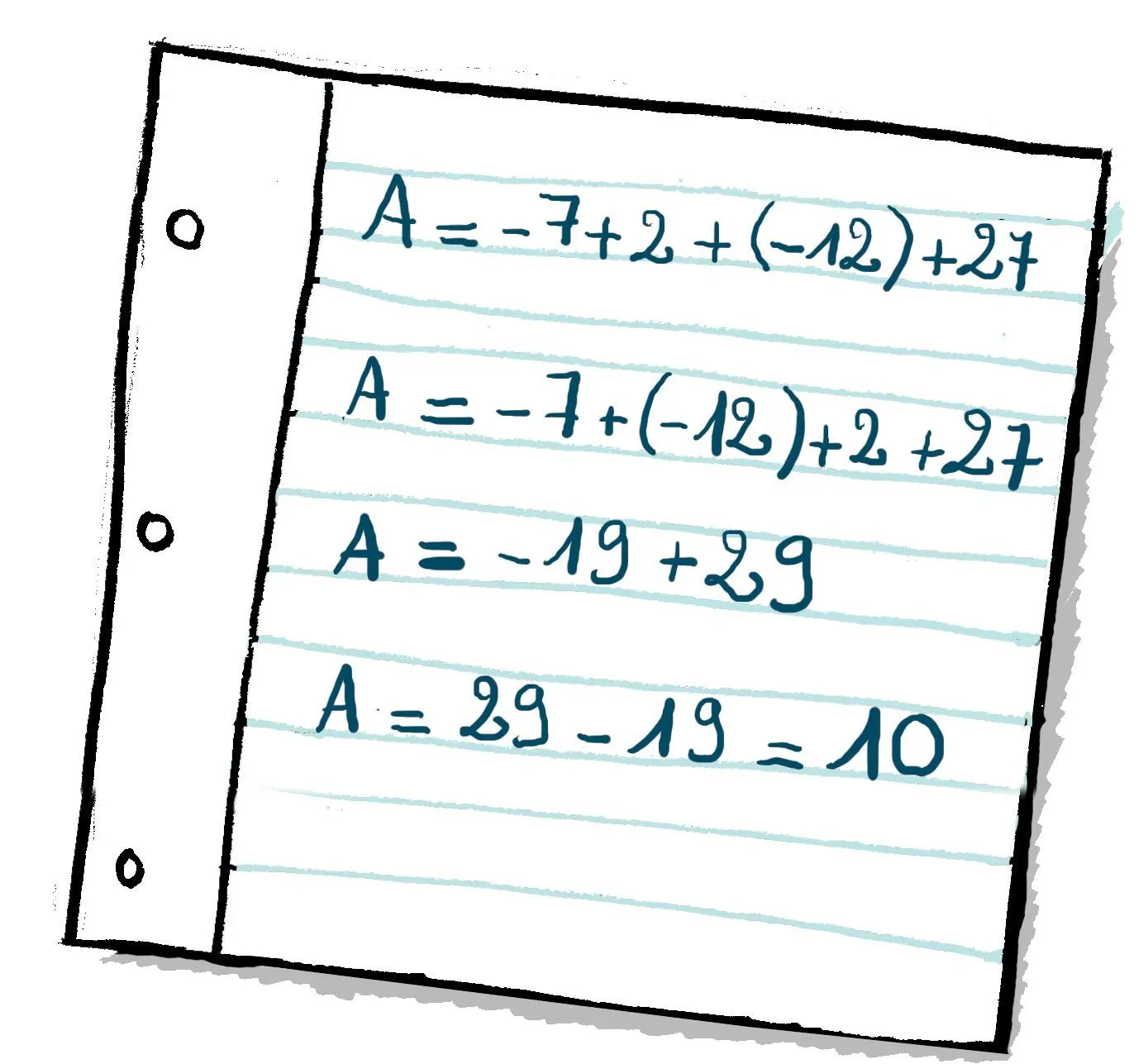
1. Analysez et expliquez la méthode utilisée par chacun. Quelle méthode vous semble ici la plus adaptée ? Pourquoi ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

55
Température.

✔ J'extrais et j'exploite les informations utiles d'un document.

Pendant une semaine, Catherine a noté les températures les plus chaudes et les plus froides de chaque journée dans un tableau. Elle veut aussi noter lʼamplitude thermique de chaque jour, cʼest-à-dire la différence entre la température maximale et la température minimale.

1. Complétez le tableau de Catherine

Jour de la semaine	L	Ma	Me	J	V	S	D
Température maximale (°C)	11	12,3	12,7	10,2	10,3	9,4	10
Température minimale (°C)	2	3,1	0,2	-1,4	-0,3	-2	0,7
Amplitude thermique (°C)	9

2. Quel jour fait-il le plus chaud ? Le plus froid ?

3. Quel jour lʼamplitude thermique a-t-elle été la plus forte ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

56
Savoir refaire
Météo.

✔ Je décompose un problème en sous-problèmes pour le simplifier et le résoudre.

1. À partir des informations suivantes, déterminez sans calculatrice la température quʼil fait à Paris, à Zagreb, à Tel-Aviv et à Moscou.

Il fait 7°C de plus à Tel-Aviv quʼà Madrid.
Il fait 8°C de moins à Zagreb quʼà Paris.
À Madrid, la température est de 11°C.
La température à Moscou est inférieure de 29°C à celle de Zagreb.
À Paris, il fait plus froid quʼà Tel-Aviv. Le thermomètre indique 16°C de moins.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

57
Savoir refaire
Hérode Antipas.

✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème.

Hérode Antipas, fils dʼHérode Ier le Grand et de Malthace la Samaritaine, est né en 21 av. J.-C. et mort en 39 ap. J.-C., après 43 ans de règne sur la Galilée et la Pérée.

1. À quel âge est-il mort ?

2. En quelle année est-il devenu roi ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

58
La démarche de Peter.

✔ J'argumente et j'échange sur une démarche mathématique.

Le zoom est accessible dans la version Premium.

1. Calculez A

= 7 - 13 + 8 - 5

2. Voici la copie de Peter. Obtient-il le bon résultat ? Expliquez sa démarche.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

59
Savoir refaire
Plongée sous-marine.

✔ Je meodélise une situation à l'aide d'un schéma, d'un tableau ou d'un arbre.

Un plongeur qui descend à de grandes profondeurs doit effectuer des paliers de décompression lorsquʼil remonte à la surface.Ces paliers dépendent de la profondeur à laquelle le plongeur descend et de la durée de la plongée.Par exemple, un plongeur qui reste une heure à 35 m de profondeur doit réaliser un palier de plusieurs dizaines de minutes à 6 m de profondeur, puis un autre à 3 m.

1. Dans lʼexemple, de combien de mètres le plongeur remonte-t-il pour atteindre le premier palier ? Le deuxième ?

2. Représentez cette situation sur un axe vertical gradué où le niveau de la mer est à 0 et les profondeurs sont représentées par des nombres négatifs.

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

60
Snooker.

✔ Je décompose un problème en sous-problèmes pour le simplifier et le résoudre.

Illustration d'une jeune femme jouant au billard

Le zoom est accessible dans la version Premium.

Voici le classement du championnat de snooker à lʼissue de lʼavant-dernière manche :

Marc : 13 points ;
Laetitia : 8 points ;
Julien : 3 points ;
Fanny : -2 points ;
Patrice : -9 points.

Lors de la dernière manche :

Marc perd 7 points ;
Fanny en gagne 6 ;
Laetitia en perd 3 ;
Patrice réalise un score de (-5)
et Julien marque 3 points de moins que Fanny.

1. Donnez le classement final du championnat, ainsi que le score de chaque concurrent.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

61
Terminus.

✔ Je sais passer du language naturel au language mathématique et inversement.

Sept personnes se sont installées dans le bus au moment où il démarre.

Au premier arrêt, 3 personnes descendent du bus et 6 personnes montent.
Au deuxième arrêt, personne ne monte mais 4 personnes descendent.
Au troisième arrêt, 9 personnes montent et 6 descendent.
Au terminus, tout le monde descend !

1. Combien de personnes descendent au terminus ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

62
Jeu vidéo.

✔ Je structure mon raisonnement.

Arthur, Frank, Momo et Laura jouent à un jeu vidéo. Arthur et Frank sont dans lʼéquipe bleue, Momo et Laura, dans lʼéquipe rouge.Chaque joueur possède un score, positif ou négatif.Le score de chaque équipe est égal à la somme des scores de ses joueurs.Lʼéquipe gagnante est celle dont le score est le plus élevé. Il reste une manche à jouer, et les scores sont les suivants :

Arthur : -38
Frank : 51
Momo : -4
Laura : -7

Lors de la dernière manche :

Laura marque 5 points ;
Frank perd 8 points ;
Momo perd 4 points de moins que Frank ;
Le nombre de points marqués par Arthur est lʼopposé de celui de Laura.

1. Déterminez le score final de chaque équipe, et déduisez-en lʼéquipe gagnante.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

63
Rome antique.

✔ Je me repère sur une droite, dans le plan ou dans l'espace.

Voici plusieurs personnages importants de la Rome antique :

Cicéron est mort en 43 av. J.-C. à 63 ans ;
Auguste est né en 63 ap. J.-C. et mort à 77 ans ;
Pline lʼAncien est mort à 56 ans, en 79 ap. J.-C ;
Tite-Live atteignit la moitié de sa vie en 21 av. J.-C. et mourut à 76 ans ;
Jules César fut assassiné à 56 ans, en 44 av. J.-C ;
Sénèque est né en 4 av. J.-C. et a vécu 69 ans.

1. Dessinez une frise chronologique.

Dessinez ici

2. Qui est né le premier ? Le dernier ?

3. Qui est mort le premier ? Le dernier ?

4. Qui a pu connaitre Jules César de son vivant ?

5. En quelle année aurait-il fallu naitre pour avoir 18 ans au moment du décès de lʼempereur Auguste ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

64
Jean et Sara font leurs comptes.

✔ Je sais passer du langage naturel au langage mathématique et inversement.

Jean avait 72,35 € sur son compte au début de lʼannée ; Sara avait une dette de 28 €. Depuis, Jean a reçu 90 € dʼargent de poche et dépensé 124,49 €. Sara a maintenant 31,14 € sur son compte.

1. Qui a le plus dʼargent sur son compte ?

2. Combien dʼargent Sara a-t-elle reçu ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

65
Comptes bancaires.

✔ Je modélise une situation à l'aide d'une expression mathématique.

Arnaud possède 53,80 € sur son compte au début du mois. Il retire 25 € pour sʼacheter un DVD. Il reçoit 30 € pour son anniversaire, mais décide de nʼen mettre que la moitié sur son compte. Julien a quant à lui une dette de 5,40 € sur son compte au début du mois.Il place donc 20 € sur son compte, puis dépense 9,90 € pour sʼacheter un tee-shirt.

1. Combien Arnaud et Julien possèdent-ils sur leur compte à la fin du mois ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

66
Traduisez en langage mathématique.

✔ Je sais passer du langage naturel au langage mathématique et inversement.

1. Écrivez

1, 5

comme la différence de deux nombres de signes opposés.

2. Écrivez

- 1, 5

comme la différence de deux nombres de signes opposés.

3. Écrivez

- 1, 5

comme la somme de deux nombres du même signe.

4. Écrivez

1, 5

comme le quotient de deux nombres négatifs.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

67
Savoir refaire
Code secret.

✔ J'émets une hypothèse.

Remplacez les triangles par les signes « + » ou « – ».
Indiquez quand il y a plusieurs solutions possibles.

1.

(Δ 3) + (Δ 4) = - 7

(Δ 3) Δ (Δ 4) = + 7

(Δ 3) Δ (Δ 4) = - 1

(Δ 3) Δ (Δ 4) = + 1

(Δ 2) \times (Δ 6) = - 12

3 \times (Δ 5) + (Δ 6) = - 9

19 Δ ((Δ 2) + (Δ 7)) = + 10

(Δ 20) \div (Δ 4) - (Δ 3) = - 8

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

68
Un long voyage.

✔ J'émets une hypothèse.

Le zoom est accessible dans la version Premium.

On se déplace dʼile en ile entre le départ et lʼarrivée. À chaque passage sur une ile, on gagne ou on perd des points.On ne peut passer quʼune fois sur chaque ile.

1. Quel est le trajet qui rapporte le plus de points ?

2. Quel est le trajet qui rapporte le moins de points ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

69
Par monts et par vaux.

✔ Je comprends et j'utilise la modélisation numérique ou géométrique d'une situation.

Photo d'un homme faisant de la randonnée

Le zoom est accessible dans la version Premium.

Crédits : Olga Danylenko/ Shutterstock

Le zoom est accessible dans la version Premium.

1. Déterminez les ordonnées des points A, B, C, D et E.

2. Les coordonnées représentent un groupe dʼamis qui font une marche dans les Alpes. Le niveau 0 correspond au point de départ de la randonnée (donc une altitude négative est possible sans pour autant être dans lʼeau !). Combien de mètres ont-ils monté ? Descendu ?

3. Quel dénivelé total ont-ils parcouru ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

70
Signe d'un produit

✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème.

1. Quel est le signe du produit

(+ 1) \times (- 2) \times (+ 3) \times ... \times (+ 999) \times (- 1000)

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

71
Signe d'un produit.

✔ Je structure mon raisonnement.

1. Quel est le signe du produit

(- 100) \times (- 99) \times (- 98) \times ... \times (+ 99) \times (+ 100)

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

72
Un troc équitable ?

Daniel et Nicolas sont deux amis qui aiment jouer au plus malin.Ainsi, Daniel propose un marché à Nicolas : « Aujourdʼhui, tu me donnes 1 €. Demain, je tʼen donne 2. Après-demain, tu mʼen donnes 3, et ainsi de suite pendant un an. Chaque fois que tu me donnes une somme, je te donne le lendemain la même somme avec un euro de plus, donc tu y gagnes. »

1. Nicolas, méfiant, se demande sʼil doit accepter. Quʼen pensez-vous ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

73
Une partie de billard.

✔ Je structure mon raisonnement.

Le zoom est accessible dans la version Premium.

Crédits : Rawit.wsm/Shutterstock

Sally, Marion, Fanny et David vont jouer au billard.Chacun prend un soda à 3,20 € et la location de la table de billard est de 12 €.Comme ils nʼont pas de petite monnaie, Sally paie toutes les boissons et Fanny paie les 12 € de la table.

1. Le lendemain, chacun a apporté assez de monnaie pour rembourser Sally et Fanny. Mais comment faire ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Tâche complexe
Quelle course !

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Énoncé

✔ J'extrais et j'exploite les informations utiles d'un document.

Julien participe à une course qui combine course à pieds et plongée en bouteille.

1. Combien de temps prendra-t-il pour faire ce parcours ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Doc. 1
Le rythme de Julien.

À terre, il lui faut :

2 minutes pour monter un dénivelé de 10 m ;
1 minute pour descendre un dénivelé de 10 m.

En mer, il lui faut :

5 minutes pour descendre un dénivelé de 10 m ;
10 minutes pour monter un dénivelé de 10 m.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Doc. 2
Caractéristiques de la course de Julien.

Il lui faut 30 minutes pour s'habiller en combinaison et préparer son matériel de plongée. Donc, quand il passe de la terre à la mer et de la mer à la terre, il perd 30 minutes.
Quand il plonge, il rase le fond de la mer.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Doc. 3
Carte.

Voici la carte de la course. Chaque ligne de niveau représente une altitude. Il y a une ligne tous les 5 m.
Sa hauteur par rapport au niveau de la mer (0) est notée à côté.
Le point culminant de la course s'élève à 65 m. Julien doit passer par tous les points notés en noir.

Le zoom est accessible dans la version Premium.

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

Oups, une coquille

j'ai une idée !

Nous préparons votre pageNous vous offrons 5 essais

Yolène

Émilie

Jean-Paul

Fatima

Sarah

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.