Nos classiques

Mathématiques Cycle 4

Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Ch. 7
Puissances
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et géométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Ch. 17
Agrandissements - réductions
Agrandissements - Réductions
Ouverturep. 367
Je découvre le chapitre
Introductionp. 368-369
J'apprends
Coursp. 370-373
Questions Flash / Je m'entraine
Exercicesp. 374-377
Problèmes résolus
Problèmesp. 378
Problèmes résolus
Problèmesp. 379
Je résous des problèmes
Exercicesp. 380-385
Exercices numériques
Exercicesp. 386
Maths autrement : Le banquet des sept sages
Travailler autrementp. 387
Je m'évalue
Exercicesp. 388
Ch. 18
Trigonométrie
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Nos dossiers d'actualité
Dossier d'actualité
Chapitre 17
Exercices

Questions Flash - Je m'entraine

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Questions flash

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

\text{ABC} est un triangle. Les droites \text{(MN)} et \text{(BC)} sont parallèles.
Cette figure servira pour les exercices 1 à 3
Graphique d'un triangle ABC

1.  Dʼaprès le théorème de Thalès...







2.  Selon le théorème de Thalès, quelle(s) égalité(s) est/sont vraie(s) ?







3.  Dans quel(s) cas peut-on calculer \textbf{BC} ?







4.  Les droites \text{(IJ)} et \text{(KL)} sont parallèles. Quelle est la mesure de \text{IO} ?
Graphique de deux droites IJ et KL

     

5.  Les points \textbf{B}, \textbf{A}, \textbf{E} sont alignés dans cet ordre, les points \textbf{C}, \textbf{A}, \textbf{D} sont alignés dans cet ordre. Les droites \textbf{(BC)} et \textbf{(ED)} sont parallèles. Quelle affirmation est vraie ?
Deux droites BC et ED







6.  Soit une figure dʼaire \textbf{16 cm}^{2}. Après une réduction, on obtient une figure dʼaire \textbf{4~cm}^{2}. Quel est le rapport de réduction ?

     
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Je m'entraine

Le théorème de Thalès
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1
Les droites de couleur sont parallèles. Donnez tous les rapports de longueurs égaux.

✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème.

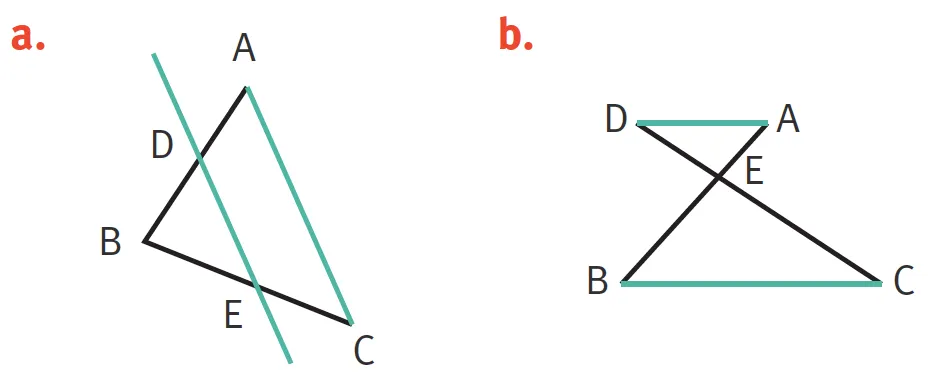Placeholder pour Diagramme géométrique: deux triangles, un avec lignes sécantes, l'autre avec segments parallèles. Points A, B, C, D, E indiqués.Diagramme géométrique: deux triangles, un avec lignes sécantes, l'autre avec segments parallèles. Points A, B, C, D, E indiqués.
1. Donnez tous les rapports de longueurs égaux.
 2. Donnez tous les rapports de longueurs égaux.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

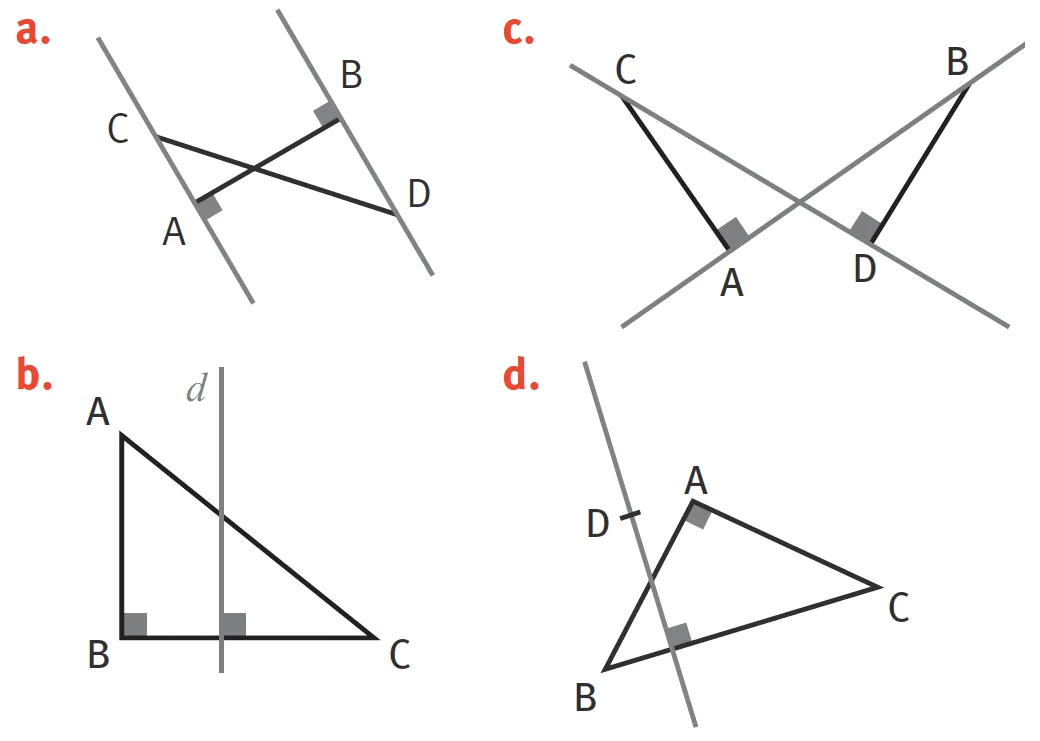
2
Justifiez.

Placeholder pour Diagramme géométrique: quatre schémas illustrent des triangles et des lignes parallèles coupées par des sécantes. Angles et propriétés géométriques sont indiqués.Diagramme géométrique: quatre schémas illustrent des triangles et des lignes parallèles coupées par des sécantes. Angles et propriétés g�éométriques sont indiqués.
1. Peut-on utiliser le théorème de Thalès dans cette situation ?
 2. Peut-on utiliser le théorème de Thalès dans cette situation ?
 3. Peut-on utiliser le théorème de Thalès dans cette situation ?
 4. Peut-on utiliser le théorème de Thalès dans cette situation ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

3
Calculez les longueurs demandées.

1. \text{(BC)} et \text{(DE)} sont parallèles. Calculez \text{AE} et \text{AC}.
Graphique d'un triangle

Calculez \text{AE}, \text{AC} et \text{DE}.
Graphique d'un triangle
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

4
Calculez les longueurs demandées.

1. \text{(AB)} et \text{(CD)} sont parallèles. Calculez \text{MB}. Que pouvez-vous dire du quadrilatère \text{ABDC} ?
Deux droites AB et CD qui sont parralèles
 2. \text{(MN)} et \text{(BC)} sont parallèles. On donne \text{AB=9~cm}, \text{AC=12~cm}, \text{BC=7~cm},\text{AM=3~cm} et \text{OB=6~cm}.
Calculez \text{AN}, \text{MN}, \text{ON}.
Deux droites AB et CD qui sont parralèles
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

5
Quelles questions poser ?

✔ J'émets une hypothèse.

Les droites \text{(SA)} et \text{(OK)} sont parallèles. On sait que \text{SA = 5~cm}, \text{KR = 7,2~cm}, \text{OR = 6,84~cm} et \text{OA = 3,8~cm}.
Les questions de cet exercice ont été effacées, mais il reste ci-dessous des calculs effectués par un élève.
En utilisant tous les calculs suivants, rédigez précisément les questions auxquelles l'élève a répondu.

Graphique d'un triangle
1. 6\text{,}84 - 3\text{,}8 = 3\text{,}04
 2. \dfrac{5\times6\text{,}84}{3\text{,}04}=11\text{,}25
 3. 7\text{,}2 + 6\text{,}84 + 11\text{,}25 = 25\text{,}29
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

6
Savoir refaire
\textbf{ABC} est un triangle rectangle en \textbf{B} tel que \textbf{AB = 6~cm} et \textbf{AC = 10~cm}.

✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème.

Graphique lié à l'exercice 11
1. Calculez \text{BC}.
 2. Le point \text{M} sur \text{[BC]} est tel que \text{BM = 3~cm}. Calculez \text{CM}.
 3. La perpendiculaire à \text{(BC)} passant par \text{M} coupe \text{[AC]} en \text{N}. Calculez \text{CN}.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

7
\textbf{ABC} est un triangle tel que \textbf{AB = 5~cm} et \textbf{AC = 8~cm}.

\text{M} est le point de \text{[AB]} tel que \text{AM = 2~cm}. On trace la parallèle à \text{[BC]} passant par \text{M} qui coupe \text{[AC]} en \text{N}.

1. Tracez une figure correspondante.

Cliquez pour accéder à une zone de dessin

2. Calculez \text{AN}.
 3. Pouvez-vous calculer \text{MN} et \text{BC} ? Exprimez \text{MN }en fonction de \text{BC}.
 4. Complétez le tableau suivant :

Valeur de \text{MN} \text{(cm)} \text{2} \text{3} \text{4} \text{5} \text{10}
Valeur de \text{BC} \text{(cm)}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

8
\textbf{PQR} est un triangle tel que \textbf{PQ = 3,6~cm}, \textbf{QR = 4,8~cm} et \textbf{PR = 6~cm}.

1. Tracez le triangle \text{PQR}.
 2. Montrez que \text{PQR} est un triangle particulier.
 3. \text{O} est le point de \text{[PQ]} tel que \text{OP = 3~cm}. On trace la parallèle à \text{(QR)} passant par \text{O} ; elle coupe \text{[RP]} en \text{M}.
 4. Montrez que \text{POM} est une réduction de \text{PQR} dont vous préciserez le rapport.
 5. Quelle est la nature de \text{POM} ?
 6. Calculez \text{PM} et \text{OM}.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

9
Savoir refaire
\textbf{AMN} est un triangle rectangle en \textbf{M}. \textbf{B} et \textbf{C} sont les symétriques respectifs de \textbf{M} et \textbf{N} par rapport à \textbf{A}.

✔ Je structure mon raisonnement

Graphique d'un traingle rectangle AMN
1. Calculez \text{AM}.
 2. Les droites \text{(BC)} et \text{(MN)} sont-elles parallèles ?
 3. Calculez \text{BC}.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

10
Le quadrilatère \textbf{ABCD} est un rectangle tel que \textbf{AB = 15~cm} et \textbf{BC = 5~cm}.

✔ Je choisis un cadre adapté (numérique, algébrique ou géométrique) pour traiter un problème.

Le point \text{M} est sur le segment \text{[CD]} tel que \text{DM = 12~cm}. \text{N} est le point d'intersection des droites \text{(AM)} et \text{(BC)}.

1. Tracez la figure en grandeur réelle.
Logo Geogebra

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

2. Calculez \text{MC} et \text{AM}.
 3. Calculez \text{CN} puis \text{BN}.
 4. Déduisez-en \text{AN} puis \text{MN}.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Les droites sont-elles parallèles ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

11
\text{DFG} est un triangle tel que \bold{DF = 7,5~cm} et \bold{DG = 5,5~cm}.

Graphique d'un triangle
E est un point de \text{[DF]} tel que \text{DE = 3,5~cm} et \text{H} un point de \text{[DG]} tel que \text{DH = 2,5~cm}.

1. Les droites \text{(EH)} et \text{(FG)} sont-elles parallèles ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

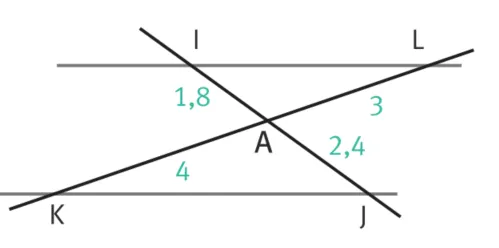
12
Les droites \bold{(JK)} et \bold{(IL)} sont-elles parallèles ?

Placeholder pour Schéma : deux droites sécantes coupant deux parallèles, angles et mesures indiqués.Schéma : deux droites sécantes coupant deux parallèles, angles et mesures indiqués.
1. Justifiez votre réponse.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

13
\textbf{AC = 10~cm}, \textbf{MC = 6~cm}, \textbf{NC = 5~cm} et \textbf{BC = 9~cm}.

✔ Je fais appel à mes connaissances pour comprendre et résoudre un problèle.

Graphique d'un triangle
1. Le triangle\text{ MNC} est-il rectangle en \text{N} ? Justifez.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

14
Triangle \textbf{ABC}.

1. Tracez un triangle \text{ABC} tel que \text{ AC = 7,5~cm}, \text{AB = 6~cm} et \text{BC = 10~cm}.Placez \text{E} sur \text{[AC]} tel que \text{CE = 3~cm} et \text{F} sur \text{[BC]} tel que \text{CF = 4~cm}.

Cliquez pour accéder à une zone de dessin

2. Les droites \text{(AB)} et \text{(EF)} sont-elles parallèles ?
 3. On trace la droite parallèle à \text{(AB)} passant par \text{C}. Cette droite coupe \text{(BE)} en \text{L}. Déterminez \text{CL}.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

15
Tracez une figure telle que les points \text{A, C, F} et \text{B, C, G} soient alignés dans cet ordre.

✔ Je modélise une situation à l'aide d'un schéma, d'un tableau ou d'un arbre.

Les droites \text{(AB)} et \text{(GF)} sont parallèles. \text{AB = 3 cm}, \text{FC = 8,4 cm} et \text{FG = 11,2 cm}.

1. Calculez la longueur \text{CA}.
2. \text{D} est le point du segment \text{[CF]} et E le point du segment \text{[GF]} tels que \text{FD = 6,3~cm} et \text{FE = 8,4~cm}.
Montrez que les droites \text{(GC)} et \text{(ED)} sont parallèles.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Agrandissements et réductions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

16
Rectangle \textbf{ABCD}.

\text{ABCD} est un rectangle dʼaire \text{12~cm}^{ 2}.

1. Tracez une représentation de \text{ABCD}.
 2. Tracez un agrandissement de rapport \text{1,5} de \text{ABCD}.

 3. Quelle est son aire ?
Cliquez pour accéder à une zone de dessin
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

17
Savoir refaire
\textbf{ABC} est un triangle isocèle en \textbf{B} avec \textbf{AB = BC = 6 cm}.

✔ Je représente des objets et des figures géométriques

\text{ H} est le pied de la hauteur issue de \text{A} et relative au côté \text{[BC]} et \text{AH = 4~cm}.

1. Faites une figure.

Cliquez pour accéder à une zone de dessin

2. Calculez lʼaire du triangle \text{ABC}.
 3. Soit \text{A'B'C'} est un agrandissement de rapport \text{3} de \text{ABC}. Quelles sont les dimensions connues de \text{A'B'C'} ? Quelle est son aire ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

18
Vers le Brevet (Amérique du Nord, 2002).

✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème.

Les deux cônes de révolution de rayons KA et IB sont opposés par le sommet. Les droites (AB) et (KI) se coupent en S et, de plus, (BI) et (KA) sont parallèles. On donne KA = 4,5 cm, KS = 6 cm et SI = 4 cm.

Graphique de deux cônes de révolution
1. Calculez \text{BI}.
 2. Calculez le volume V_1 du cône 1. (Donnez la valeur exacte puis la valeur arrondie au cm^{3}.)
 3. Le cône 2 est une réduction du cône 1. Quel est le coefficient de réduction ?
 4. Déduisez-en le volume V_2 du cône 2.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

19
\textbf{[AB]} est un segment tel que \textbf{AB = 5~cm}.

1. Tracez un segment \text{[EF]}, la réduction de \text{[AB]} de rapport \text{0,7}.
 2. Tracez un segment \text{[IJ]}, lʼagrandissement de \text{[AB]} de rapport \text{1,5}.
Cliquez pour accéder à une zone de dessin
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

20
On considère la figure suivante.

Figure d'un triangle
1. Démontrez que les droites \text{(EA)} et \text{(FM)} sont parallèles.
 2. On appelle r le rapport dʼagrandissement qui transforme le triangle \text{PAE} en triangle \text{PMF} et m le rapport de réduction qui transforme le triangle \text{PMF} en triangle \text{PAE}. Calculez r et m.
3. Calculez \text{EA} et \text{FM}.
 4. Exprimez l'aire du triangle \text{PMF} en fonction de celle du triangle \text{PAE} puis calculez-les.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Parcours de compétences

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Énoncé

✔ Jʼémets une hypothèse.

Yasmine a un câble électrique dont elle ne connait pas la longueur et 5 boules lumineuses qu'elle souhaiterait répartir de manière régulière sur sa guirlande. Mattéo lui assure qu'il peut utiliser le théorème de Thalès pour l'aider. Il lui apporte un mètre ruban d'un mètre de longueur et deux équerres. Il les positionne ainsi :

Figure d'un triangle
Comment fonctionne la technique que propose Mattéo à sa cousine ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Niveau 1

Je sais ce qu'est une hypothèse et quel est son rôle dans une démarche mathématique.

Coup de pouce
Cherchez dans le dictionnaire la définition du terme hypothèse et regardez dans les problèmes résolus comment elles sont utilisées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Niveau 2

Je comprends l'hypothèse qui m'est proposée.

Coup de pouce
Utilisez le mètre ruban de Mattéo dont on connait la longueur et découpez-le en autant de morceaux que nécessaires.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Niveau 3

Je propose une hypothèse.

Coup de pouce
Pourquoi a-t-on besoin des équerres de Mattéo à votre avis ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Niveau 4

Je construis une hypothèse et je propose une solution pertinente pour la valider.

Coup de pouce
Formulez votre hypothèse et expliquez comment vous pouvez la tester.

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.