Chapitre 17
J'apprends
Agrandissements - Réductions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AAgrandissements et réductions
Je perfectionne
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Propriétés des agrandissements - réductions
Propriétés
Dans un agrandissement ou une réduction de rapport k > 0 :
(1) : agrandissement de rapport 2
(2) : réduction de rapport \frac{1}{2}

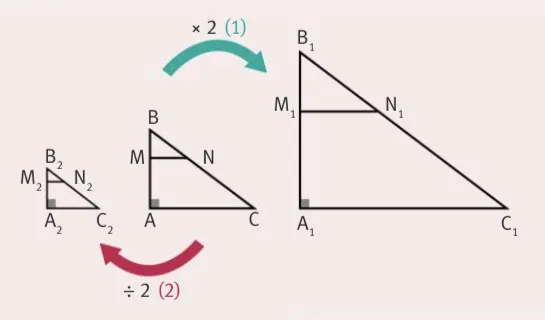
- Les longueurs sont multipliées par k ;
- Les angles sont conservés ;
- La perpendicularité et le parallélisme sont conservés.
(1) : agrandissement de rapport 2
(2) : réduction de rapport \frac{1}{2}


Exercices n° p. 376 - 377.
- Si k > 1, alors on a un agrandissement.
- Si 0 \lt k \lt 1, alors on a une réduction.
J'applique
Consigne :
Le losange EBGF est une réduction du losange ABCD. On sait que AB = 14 cm et EB = 7 cm.
Quel est le rapport de réduction ?
Le losange EBGF est une réduction du losange ABCD. On sait que AB = 14 cm et EB = 7 cm.
Quel est le rapport de réduction ?

Le losange EBGF est une réduction du losange ABCD, donc leurs longueurs sont proportionnelles. On note k le coefficient de proportionnalité :
k = \dfrac{\text{EB}}{\text{AB}} = \dfrac{7}{14} = 0\text{,}5
Le losange EBGF est une réduction de rapport 0,5 du losange ABCD.
Consigne :
C est un cône de rayon 2 cm. Après une réduction de rapport 0,75, on obtient un cône C'. Quel est le rayon de la base de C' ?
Correction :
Soit r le rayon de la base du cône C et r' celui de la base de C'.
C' est une réduction de rapport 0,75 de C donc :
r' = r \times 0\text{,}75
r' = 2 \times 0\text{,}75 = 1\text{,}5
Le rayon du cône C' mesure 1,5 cm.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Effets sur les périmètres et aires
Propriétés
Dans un agrandissement ou une réduction de rapport k > 0 :
- La longueur d'un segment est multipliée par k ;
- L'aire d'une surface est multipliée par k^2 ;
- Le volume d'un solide est multiplié par k^3.
J'applique
Consigne :
P est une pyramide de hauteur 4 cm et de volume 20 cm3. Par une réduction, on obtient une pyramide P' de hauteur 3 cm. Quel est son volume ?
Correction :
P est une pyramide de hauteur 4 cm et de volume 20 cm3. Par une réduction, on obtient une pyramide P' de hauteur 3 cm. Quel est son volume ?
Correction :
- Calcul du rapport de réduction :
k = \dfrac{\text{hauteur de }P'}{\text{hauteur de }P} = \dfrac{3}{4} = 0\text{,}75 - Calcul du volume de P' :
20 \times k^3 = 20 \times 0\text{,}75^3 = 8\text{,}4375
La pyramide P' a un volume d'environ 8,44 cm3.
Consigne :
a. ABC est un triangle rectangle en A tel que AB = 3 cm et AC = 4 cm. Calculez son aire.
b. IJK est un agrandissement du triangle ABC de rapport 3. Quelle est son aire ?
Correction :
a. \text{Aire}_{\text{ABC}} = \dfrac{\text{AB} \times \text{AC}}{2} = \dfrac{3 \times 4}{2} = 6
Donc ABC a une aire de 6 cm2.
b. Les aires sont multipliées par 32.
\text{Aire}_{\text{IJK}} = \text{Aire}_{\text{ABC}} \times 3^2 = 6 \times 3^2 = 54
Donc IJK a une aire de 54 cm2.
a. ABC est un triangle rectangle en A tel que AB = 3 cm et AC = 4 cm. Calculez son aire.
b. IJK est un agrandissement du triangle ABC de rapport 3. Quelle est son aire ?
Correction :
a. \text{Aire}_{\text{ABC}} = \dfrac{\text{AB} \times \text{AC}}{2} = \dfrac{3 \times 4}{2} = 6
Donc ABC a une aire de 6 cm2.
b. Les aires sont multipliées par 32.
\text{Aire}_{\text{IJK}} = \text{Aire}_{\text{ABC}} \times 3^2 = 6 \times 3^2 = 54
Donc IJK a une aire de 54 cm2.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BÉnoncé du théorème de Thalès
Je perfectionne
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Énoncé du théorème
Théorème
(BM) et (CN) sont deux droites sécantes en A.
Si les droites (BC) et (MN) sont parallèles alors
\dfrac{\text{A{\color{#5BA49B}M}}}{\text{A{\color{#5F3E82}B}}}=\dfrac{\text{A{\color{#5BA49B}N}}}{\text{A{\color{#5F3E82}C}}}=\dfrac{\text{{\color{#5BA49B}MN}}}{\text{{\color{#5F3E82}BC}}}.

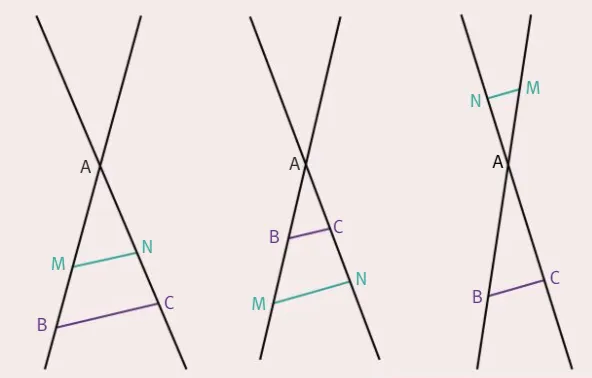
Si les droites (BC) et (MN) sont parallèles alors
\dfrac{\text{A{\color{#5BA49B}M}}}{\text{A{\color{#5F3E82}B}}}=\dfrac{\text{A{\color{#5BA49B}N}}}{\text{A{\color{#5F3E82}C}}}=\dfrac{\text{{\color{#5BA49B}MN}}}{\text{{\color{#5F3E82}BC}}}.


Exercices n° p. 374.
Remarque : Dans une configuration de Thalès, les longueurs des deux triangles formés sont proportionnelles. Les quotients définis par le théorème sont égaux au coefficient de proportionnalité : k = \dfrac{\text{AM}}{\text{AB}}=\dfrac{\text{AN}}{\text{AB}}=\dfrac{\text{MN}}{\text{BC}}. Chaque triangle est donc un agrandissement ou une réduction de lʼautre de rapport k.
Consigne :
Dans les deux configurations suivantes, les droites colorées sont parallèles. Quels sont les quotients égaux ?
Correction :
a. \dfrac{\text{IA}}{\text{IJ}} = \dfrac{\text{IB}}{\text{IK}} = \dfrac{\text{AB}}{\text{JK}}
b. \dfrac{\text{GF}}{\text{GN}} = \dfrac{\text{GE}}{\text{GM}} = \dfrac{\text{EF}}{\text{MN}}
J'applique
Consigne : Dans les deux configurations suivantes, les droites colorées sont parallèles. Quels sont les quotients égaux ?
a.


b.


a. \dfrac{\text{IA}}{\text{IJ}} = \dfrac{\text{IB}}{\text{IK}} = \dfrac{\text{AB}}{\text{JK}}
b. \dfrac{\text{GF}}{\text{GN}} = \dfrac{\text{GE}}{\text{GM}} = \dfrac{\text{EF}}{\text{MN}}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Utilisation du théorème de Thalès
Méthode
Pour déterminer une longueur manquante dans une configuration de Thalès, on écrit dʼabord les quotients égaux et on calcule ensuite la longueur manquante par proportionnalité.
Exercices n° p. 375 - 376.
Aide
On peut utiliser un tableau de proportionnalité ou directement lʼégalité des produits en croix.
J'applique
Consigne : Les droites (BC) et (DE) sont sécantes en A. Les droites (BD) et (EC) sont parallèles. Calculez AE et BD. (Les unités sont en cm.)
Correction :
- On identifie la configuration de Thalès, les droites (BC) et (DE) sont sécantes en A et les droites (BD) et (EC) sont parallèles.
- On applique le théorème, d'après le théorème de Thalès \dfrac{\text{AD}}{\text{AE}} = \dfrac{\text{AB}}{\text{AC}} = \dfrac{\text{BD}}{\text{EC}}.
- On remplace par les longueurs connues : \dfrac{2\text{,}8}{\text{AE}} = \dfrac{3\text{,}5}{10\text{,}5} = \dfrac{\text{BD}}{15}.
- On écrit lʼégalité des produits en croix : 3\text{,}5 \times \text{AE} = 10\text{,}5 \times 2\text{,}8 d'où \text{AE} = \dfrac{10\text{,}5 \times 2\text{,}8}{3\text{,}5} = 8\text{,}4.
Donc [AE] mesure 8,4 cm.
De même, 10\text{,}5 \times \text{BD} = 3\text{,}5 \times 15 donc \text{BD} = \dfrac{15 \times 3\text{,}5}{10\text{,}5} = 5. Donc [BD] mesure 5 cm.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CLa réciproque du théorème de Thalès
Je perfectionne
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Énoncé de la réciproque
Réciproque du théorème
Les points M, A, B et N, A, C sont alignés dans le même ordre.
Si \dfrac{\text{AM}}{\text{AB}}=\dfrac{\text{AN}}{\text{AC}} alors les droites (MN) et (BC) sont parallèles.
Si \dfrac{\text{AM}}{\text{AB}}=\dfrac{\text{AN}}{\text{AC}} alors les droites (MN) et (BC) sont parallèles.

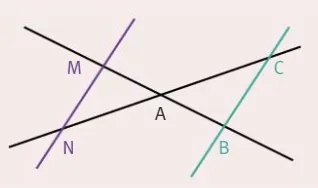
Exercices n° p. 376.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Utilisation de la réciproque
Méthode
Les droites (MN) et (AB) sont-elles parallèles ?
- On étudie la configuration. Les points O, M, A et O, N, B sont alignés dans le même ordre.
- On calcule séparément les quotients \dfrac{\text{OM}}{\text{OA}} et \dfrac{\text{ON}}{\text{OB}}.
- On compare.
- Si \dfrac{\text{OM}}{\text{OA}}=\dfrac{\text{ON}}{\text{OB}}, on utilise la réciproque du théorème de Thalès et on conclut que les droites (AB) et (MN) sont parallèles.
- Si \dfrac{\text{OM}}{\text{OA}} \ne \dfrac{\text{ON}}{\text{OB}}, l'égalité de Thalès n'est pas vérifiée. On conclut que les droites (AB) et (MN) ne sont pas parallèles.
Exercices n° p. 376.
J'applique
Consigne :
Les droites (AN) et (BM) sont sécantes en I. On a IA = 6 cm, IB = 8 cm, IM = 6 cm et IN = 4,5 cm.
Les droites (AB) et (MN) sont-elles parallèles ?
Correction :
Les points A, I, N et B, I, M sont alignés dans le même ordre.
\dfrac{\text{IN}}{\text{IA}} = \dfrac{4\text{,}5}{6} = \dfrac{3}{4} et \dfrac{\text{IM}}{\text{IB}} = \dfrac{6}{8} = \dfrac{3}{4} donc \dfrac{\text{IN}}{\text{IA}} = \dfrac{\text{IM}}{\text{IB}}
D'après la réciproque du théorème de Thalès, les droites (AB) et (MN) sont parallèles.
Les droites (AN) et (BM) sont sécantes en I. On a IA = 6 cm, IB = 8 cm, IM = 6 cm et IN = 4,5 cm.
Les droites (AB) et (MN) sont-elles parallèles ?
Correction :
Les points A, I, N et B, I, M sont alignés dans le même ordre.
\dfrac{\text{IN}}{\text{IA}} = \dfrac{4\text{,}5}{6} = \dfrac{3}{4} et \dfrac{\text{IM}}{\text{IB}} = \dfrac{6}{8} = \dfrac{3}{4} donc \dfrac{\text{IN}}{\text{IA}} = \dfrac{\text{IM}}{\text{IB}}
D'après la réciproque du théorème de Thalès, les droites (AB) et (MN) sont parallèles.

Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

