Mathématiques Cycle 4
Mes Pages
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Ch. 7
Puissances
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et géométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Ch. 17
Agrandissements - réductions
Ch. 18
Trigonométrie
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Chapitre 17
Je découvre le chapitre
Agrandissements - réductions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 1Estimer la hauteur d'un monument
Je perfectionne
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Compétence
Je comprends la modélisation numérique ou géométrique d'une situation
Yasmine et Mattéo veulent estimer la hauteur du Mont Saint-Michel.
Pour cela, Yasmine est à 3,7 km du Mont. Elle place une règle à 60 cm devant ses yeux et l'aligne avec le Mont Saint-Michel. Sur sa règle, le sommet du Mont Saint-Michel coïncide avec la graduation 1,5 cm.
Modélisez la situation présentée ci-dessus et placez les longueurs données dans l'énoncé en utilisant la même unité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Partie 1 Modéliser la situation
1
Modélisez la situation présentée ci-dessus et placez les longueurs données dans l'énoncé en utilisant la même unité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Partie 2 Découverte du théorème de Thalès
Voici ce quʼa dessiné Mattéo.
1
Comparez les triangles ABE (en vert) et ACD (en noir) : Ont-ils les mêmes longueurs ? Ont-ils les mêmes angles ?
2
Complétez alors le tableau de proportionnalité (en faisant attention aux unités). Déduisez-en la longueur CD et donc la hauteur du Mont Saint-Michel.| Triangle | Côté | Longueur (en cm pour ABE, en km pour ACD) |
| Triangle ABE | AB |
|
| BE |
| |
| AE |
| |
| Triangle ACD | AC |
|
| CD |
| |
| AD |
|
3
Avec ce que vous avez vu plus haut, complétez lʼénoncé du théorème de Thalès : Dans les triangles ABE et ACD, les droites (BE) et (CD) sont parallèles, donc :\dfrac{AB}{AC} = \dfrac{\ldots}{\ldots} = \dfrac{\ldots}{\ldots}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Partie 3 À vous de jouer !
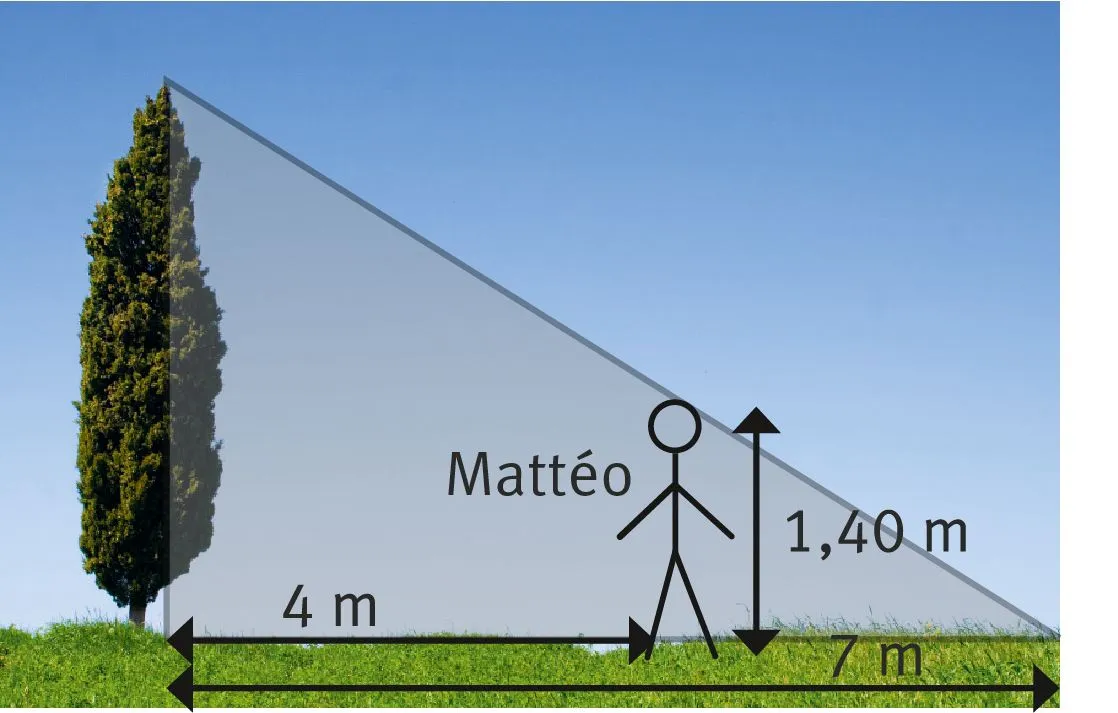
Mattéo et Yasmine s'amusent à essayer de calculer la hauteur d'un arbre. Mattéo, qui mesure 1,40 m, se place à 4 m de l'arbre, dans l'ombre que celui-ci projette. Yasmine mesure que l'ombre fait 7 m de long.
1
En modélisant la situation sur un schéma, aidez Yasmine et Mattéo à calculer la hauteur du sapin.
Coup de pouce
- Faites un shéma.
- Écrivez la formule de Thallès.
- Complétez toutes les longueurs mesurables dans la formule.
- Calculez la hauteur de l'arbre en utilisant un produit en croix.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
