Questions Flash - Je m'entraine

✔ J'utilise des cas particuliers pour orienter ma démarche de résolution

Si l'on évalue l'expression 0\text{,}2x-1\text{,}7x+2\text{,}7x-1\text{,}2 avec les nombres 5 ; 10 ; 6,25 ; 4 ; 2,75 et 9 alors on obtient un résultat qui est le double d'un autre.

1. De quels nombres s'agit-il ?

1.  L'égalité (-2x+5) = (7x-13) (2x + 5) est-elle vraie pour x = 1 ; x = 2 et x = 3 ?

2.  L'égalité (-x + 5) = (3x - 17) est-elle vraie pour x=\dfrac{7}{2} ; \dfrac{9}{2} et \dfrac{11}{2} ?

✔ Je mène à bien un calcul littéral

Le lien entre le diamètre d et le rayon r d'un cercle est donné par la formule d = 2r. Pour calculer le périmètre P, on applique la formule P = 2\pi r.

1. Complétez le tableau suivant.

✔ Je mène à bien un calcul littéral

Appliquez les formules d = 2r, P = 2\pi r et A = \pi r^2.

1. Complétez le tableau suivant.

1.  z = 2

2.  z = 8

3.  z = 4\text{,}5

Utilisez la formule P = 2 \pi r.

1.  r = 6 cm

2.  r = 20 mm

3.  r = 5 dm

4.  r = 1 m

✔ Je comprends la modélisation numérique ou géométrique d'une situation. 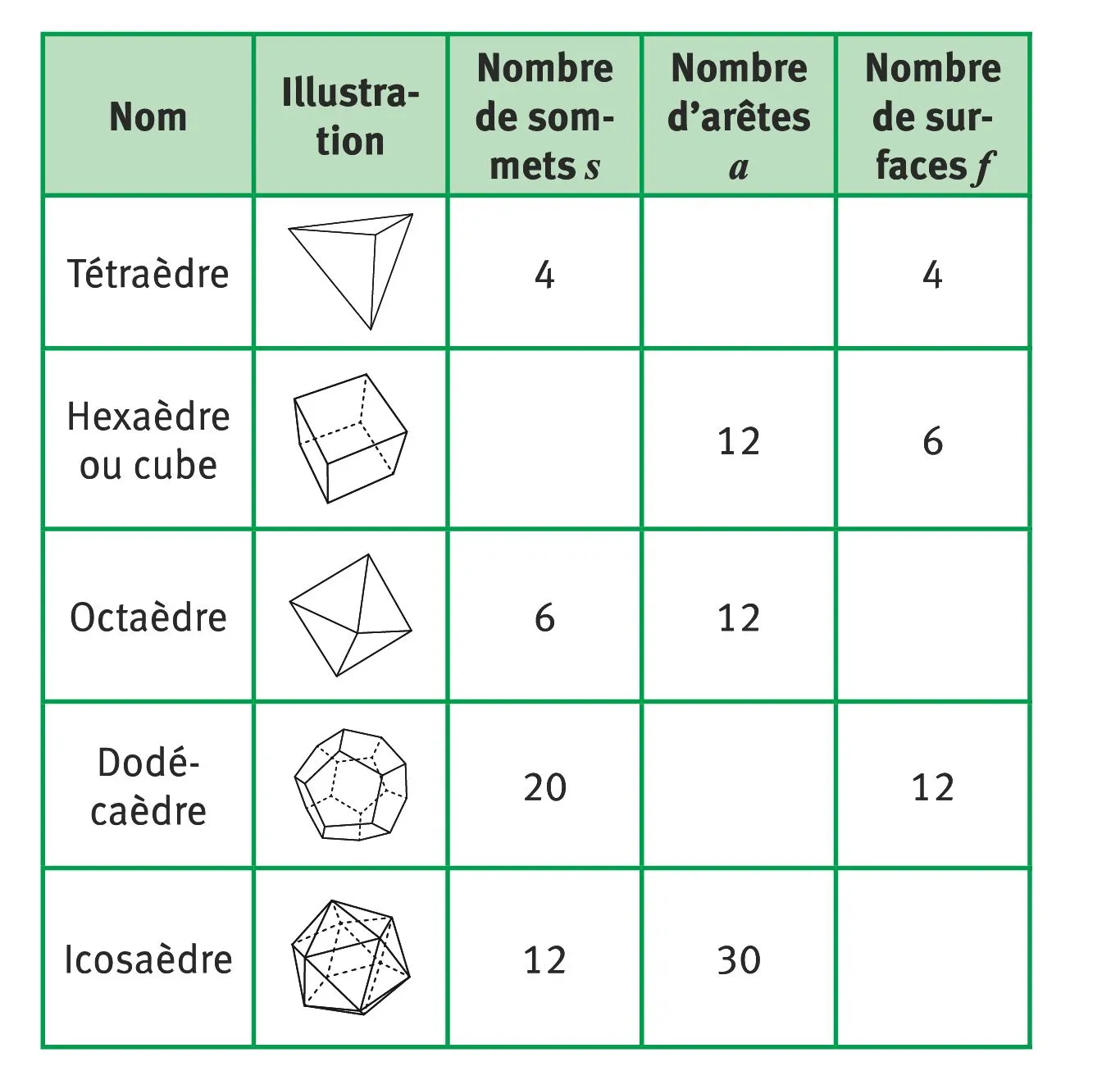Appliquez la formule s - a + f = 2 pour compléter le tableau ci-contre.

1. Complétez le tableau suivant.

1.  Tracez le rectangle ci-dessus pour z = 3\:\text{cm}. Calculez son périmètre et son aire.

2.  Tracez le rectangle ci-dessus pour z = 1\text{,}5\:\text{cm}. Calculez son périmètre et son aire.

1.  Quelle est la somme de longueurs des 12 arêtes de P ?

2.  Quel est le volume de P ?

3.  Quelle est la somme des aires des 6 faces de P ?

✔ Je modélise une situation à l'aide d'une expression mathématique.

« La distance de freinage d est le centième du carré de la vitesse v. »

1. Exprimez cette règle par une formule.

On peut donc calculer l'aire de la base avec la formule A_\text{base} = \pi \times r^2 où r est le rayon du cylindre. On peut calculer le volume avec la formule V = A_\text{base} \times h ou encore V = \pi \times r^2 \times h, où h est la hauteur du cylindre.

1. Complétez le tableau.

1. Exprimez le nombre de pages qu'il lui reste à lire en fonction du nombre de pages qu'elle a déjà lues.

Alix veut acheter trois bracelets au même prix et trois paires de boucles d'oreilles au même prix. Les bracelets n'ont pas le même prix que les boucles d'oreilles.

1. Donnez deux expressions littérales différentes du prix qu'elle doit payer.

Un kg de Golden coute 2 € ; un kg de Granny Smith coute 0,50 € de plus.

1. Combien paye Émilie selon les quantités de chaque variété qu'elle choisit ? Donnez le résultat sous forme d'une expression littérale.

✔ Je modélise une situation à l'aide d'une expression mathématique.

Zoé et Clémentine vont dans une fête foraine où le prix dʼentrée est égal au nombre d'années qu'on a.

1. Exprimez en fonction de x, de deux façons différentes, le prix qu'elles vont payer à la caisse.

1.  De quelle longueur de ficelle a-t-on besoin pour ficeler le paquet suivant de longueur 40 cm, de largeur 30 cm et de hauteur 10 cm, de la façon indiquée, sans compter les nœuds ?

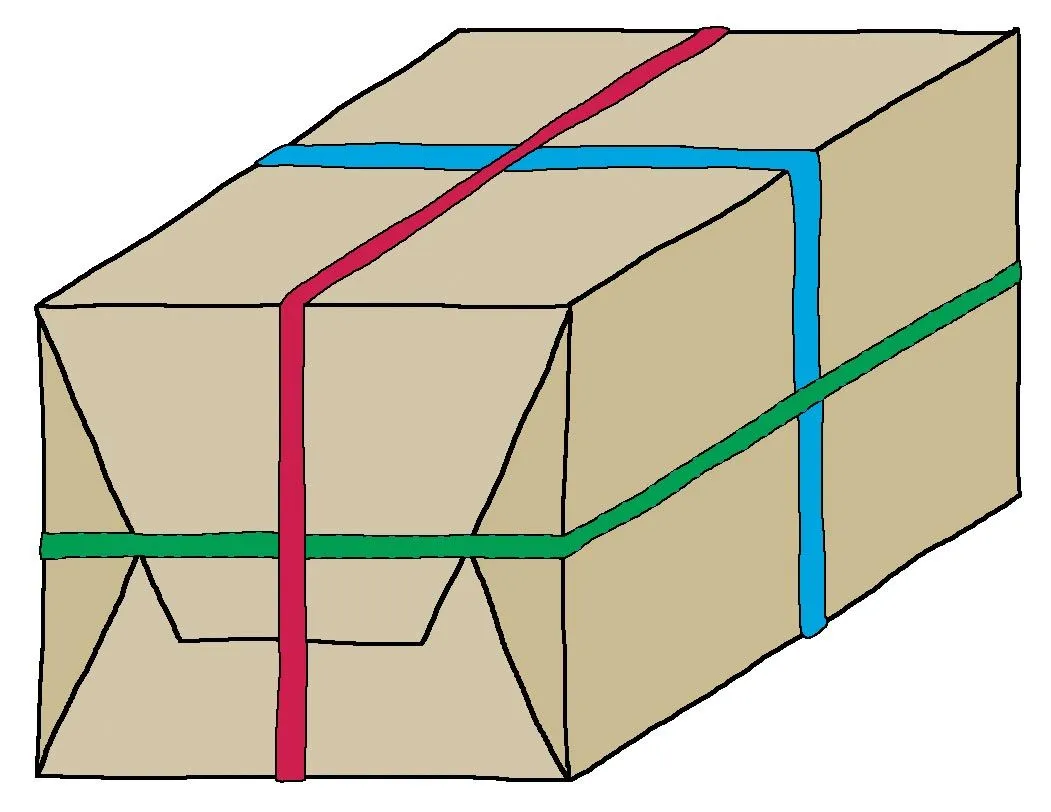
Coup de pouce

Commencez par calculer séparément les longueurs des ficelles rose, bleue et verte.

2.  Donnez la longueur de la ficelle en fonction des dimensions L, l et h du paquet.

✔ Je sais passer du language naturel au language mathématique et inversement.

1.  Le produit de 8 par le nombre que j'ai choisi est égal à 40.

2.  On obtient \dfrac{3}{4} quand on divise le nombre que j'ai choisi par 6.

3.  La différence entre 20 et le nombre que j'ai choisi est égale à -4.

4.  Quand on multiplie le nombre que j'ai choisi par 3, on obtient la somme des nombres 7 et 11.

1.  modéliser l'aire d'un rectangle ?

2.  modéliser l'aire d'un carré ?

3.  modéliser le volume d'un cube ?

4.  modéliser le volume d'un parallélépipède rectangle ?

5.  modéliser le périmètre d'un triangle équilatéral ?

6.  modéliser le périmètre d'un triangle isocèle ?

7.  modéliser le périmètre d'un trapèze ?

1.  Déterminez les mesures des côtés \text{NO} et \text{IO} en fonction de a et b.

2.  Quel est le périmètre de la figure ? (Donnez le résultat sous la forme d'une expression littérale réduite.)

1.  La longueur AB

2.  Le périmètre de cette figure

3.  L'aire de cette figure.

Proposez une expression littérale qui prend les valeurs de la deuxième ligne quand on donne à la variable les valeurs de la première ligne.

1.  Pour ce tableau
a.

2.  Pour ce tableau
b.

3.  Pour ce tableau
c.

1. Modélisez le volume de ce parallélépipède rectangle par une expression littérale.

✔ Je combine de façon appropriée les différents outils de calcul.

1. Modélisez le volume de ce parallélépipède rectangle à lʼaide dʼune expression littérale développée et réduite au maximum.

✔ Je mène à bien un calcul littéral.

1.  4x + 8 et (2x + 4) \times 2

2.  a - b et b - a

3.  y - 2z et (y - z) \times 2

4.  q + 2 - p et q - p + 2

5.  3x^2 et 6x

6.  3 - a - 7 et 3 - (a - 7)

7.  (x + 4) \div 4 et x + 1

8.  (2 \times 3)x et (2x)\times 3

1.  x + 7 + (y - 4) et y + x + 3

2.  4 \times (y + 8) - 2 et 4 \times y + 30

3.  3 \times y - (2 - x + y) \times 5 et -2 \times (y - x) - 10 + 3 \times x