✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème
✔ Je décompose un problème en sous-problèmes pour le simplifier et le résoudre

Le zoom est accessible dans la version Premium.

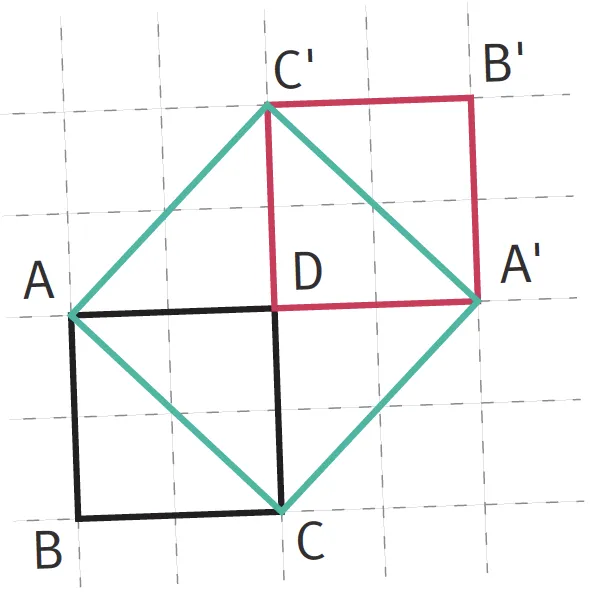Montrez que ACA'C' est un carré.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Méthode 1

Pour prouver qu'un quadrilatère est un carré, on va montrer :

Que ses diagonales se coupent en leur milieu : c'est un parallélogramme ;
Que ses diagonales se coupent perpendiculairement : c'est un losange ;
Que ses diagonales sont de même longueur : c'est un rectangle.

D'après le cours, un parallélogramme qui est à la fois un rectangle et un losange est un carré.

Corrigé 1

A' est le symétrique de A par rapport à D, donc AD = DA'. De même, DC = DC'. [AA'] et [CC'] se coupent en D qui est leur milieu, donc ACA'C' est un parallélogramme.
ABCD est un carré donc \widehat{\text{ADC}} = 90^{\circ}. Donc les diagonales [AA'] et [CC'] se coupent perpendiculairement. Donc ACA'C' est un losange.
ABCD est un carré donc AD = DC. On sait de plus que AD = DA' et DC = DC'. D'où AA' = CC'. Les diagonales de ACA'C' sont de même longueur, c'est donc un rectangle.
ACA'C' est à la fois un losange et un rectangle : c'est donc un carré.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Méthode 2

Pour prouver qu'un quadrilatère est un carré, on va montrer :

Que ses côtés sont deux à deux de même longueur : c'est un parallélogramme ;
Que deux côtés consécutifs sont de même longueur : c'est un losange ;
Qu'il possède un angle droit : c'est un rectangle.

D'après le cours, un parallélogramme qui est à la fois un rectangle et un losange est un carré.

Corrigé 2

[A'C'] est le symétrique de [AC] par rapport à D, donc A'C' = AC. C est le symétrique de C' par rapport à D, donc l'image de [AC'] par la symétrie de centre D est [A'C], d'où AC' = A'C. Les côtés opposés de ACA'C' sont deux à deux de même longueur, donc ACA'C' est un parallélogramme.
DC = DC' et (AD) et (CC') sont perpendiculaires donc C' est l'image de C par la symétrie d'axe (AD). Donc AC = AC', donc ACA'C' est un losange.
ADC est un triangle isocèle rectangle en D. Donc \widehat{\text{DAC}} = 45^{\circ}. C' est le symétrique de C par rapport à (AD) donc \widehat{\text{DAC}^{\prime}} = 45^{\circ}.
Ainsi \widehat{\text{CAC}^{\prime}} = 90^{\circ}. ACA'C' est un parallélogramme avec un angle droit : c'est donc un rectangle.
ACA'C' est à la fois un losange et un rectangle : c'est donc un carré.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

52
Problème similaire
Triangle rectangle et losange.

Le zoom est accessible dans la version Premium.

Soit le triangle ABC rectangle en A.

1. Reproduisez et placez le symétrique C' de C par rapport à (AB) et B' de B par rapport à (AC).

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

2. Montrez que C'BCB' est un losange.

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

Oups, une coquille

j'ai une idée !

Nous préparons votre pageNous vous offrons 5 essais

Yolène

Émilie

Jean-Paul

Fatima

Sarah

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Problèmes résolus

51Soit ABCD un carré et A'B'C'D son symétrique par rapport à D.

52Problème similaireTriangle rectangle et losange.

GeoGebra

Une erreur sur la page ? Une idée à proposer ?

Nous préparons votre pageNous vous offrons 5 essais

51
Soit ABCD un carré et A'B'C'D son symétrique par rapport à D.

52
Problème similaire
Triangle rectangle et losange.