Mathématiques Cycle 4
Mes Pages
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Ch. 7
Puissances
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et géométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Ch. 17
Agrandissements - réductions
Ch. 18
Trigonométrie
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Chapitre 14
Problèmes résolus
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49Démontrez le parallélisme.
✔ Je structure mon raisonnement
✔ J'envisage plusieurs méthodes de résolution
A, B et C ne sont pas alignés. Posez A' et B', les symétriques de A et B par rapport à C.
Montrez que (AB) et (A'B') sont parallèles.
✔ J'envisage plusieurs méthodes de résolution
A, B et C ne sont pas alignés. Posez A' et B', les symétriques de A et B par rapport à C.
Montrez que (AB) et (A'B') sont parallèles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1
Pour montrer le parallélisme de deux droites.
On peut s'attacher à démontrer que deux angles alternes-internes ou correspondants sont égaux.
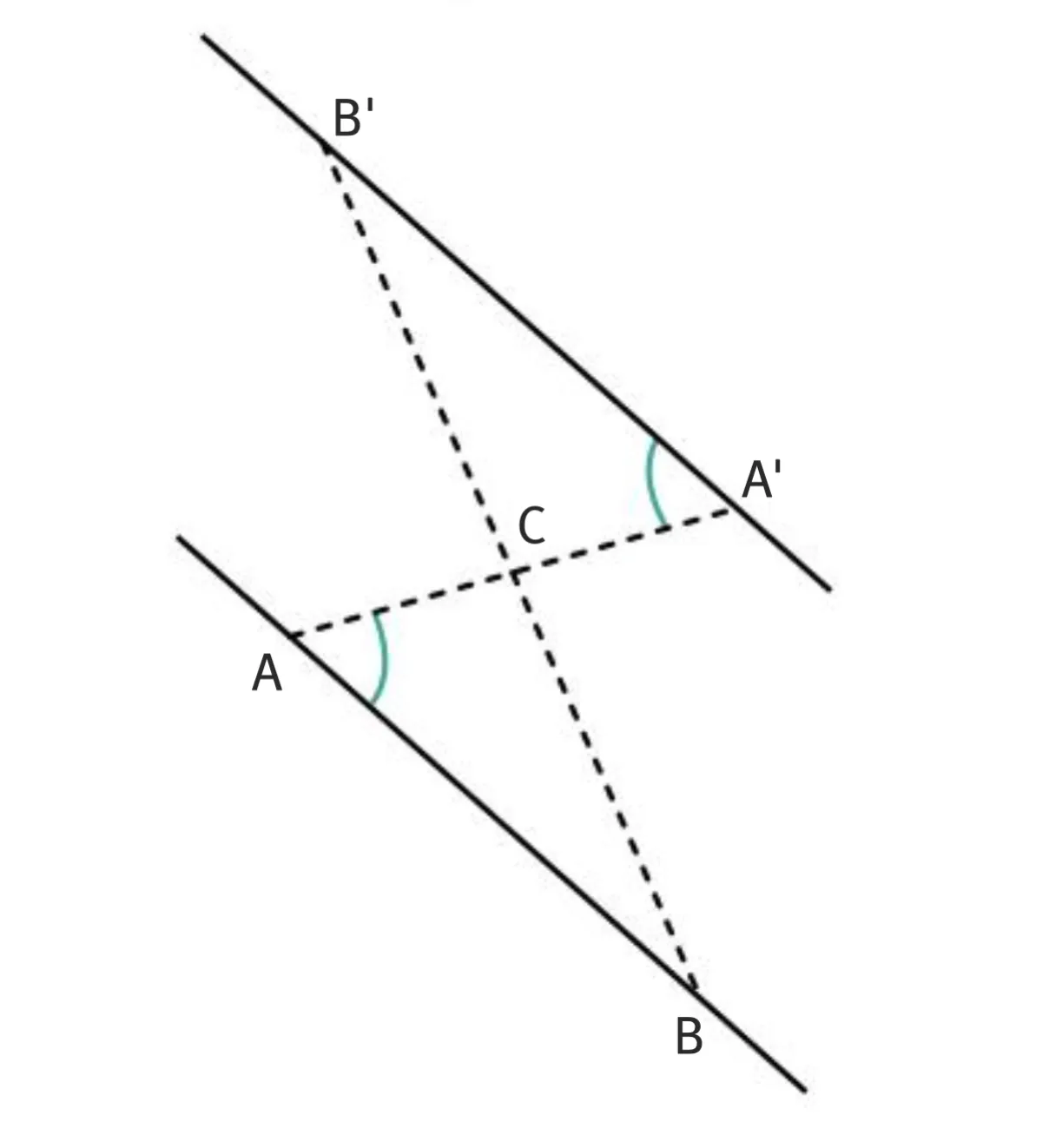
On peut s'attacher à démontrer que deux angles alternes-internes ou correspondants sont égaux.
Corrigé 1
- A' et B' sont respectivement les images de A et B par la symétrie de centre C. Donc le triangle A'B'C est l'image de ABC par la symétrie de centre C.
- La symétrie centrale conserve les mesures des angles donc \widehat{\text{BAC}} et \widehat{\text{CA}^{\prime}\text{B}^{\prime}} sont égaux.
- Or ils sont alternes-internes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2
Pour montrer que deux droites sont parallèles, on peut aussi d'abord construire un quadrilatère dont deux arêtes appartiennent aux droites. Il faut alors montrer que ce quadrilatère est un parallélogramme et enfin en déduire que les droites sont parallèles.
Corrigé 2
- On sait que les symétries centrales préservent les distances.
Donc AC = A'C et BC = B'C. - Les diagonales du quadrilatère ABA'B' se coupent en C qui est leur milieu, donc ABA'B' un parallélogramme.
- Or les côtés d'un parallélogramme sont parallèles deux à deux, donc (AB) et (A'B') sont parallèles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
50Problème similaire Cercle, triangle et quadrilatère.
C est un cercle de centre O et de rayon r = 6 \text{,} 2 cm. A et B sont deux points de ce cercle.
1. Construisez le point M, symétrique de A par rapport à O, et le point N, symétrique de B par rapport à O. Justifiez que M et N appartiennent au cercle.
2. Quelle est la nature du quadrilatère ABMN ? Justifiez.
1. Construisez le point M, symétrique de A par rapport à O, et le point N, symétrique de B par rapport à O. Justifiez que M et N appartiennent au cercle.
GeoGebra
2. Quelle est la nature du quadrilatère ABMN ? Justifiez.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
