Mathématiques Cycle 4
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Ch. 7
Puissances
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et géométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Ch. 17
Agrandissements - réductions
Ch. 18
Trigonométrie
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Chapitre 14
J'apprends
Angles et droites parallèles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AAngles et parallélisme
Je découvre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Droites parallèles
Rappels
Deux droites qui ont un seul point commun sont dites sécantes.
Deux droites qui ne sont pas sécantes sont parallèles.
Deux droites qui ont deux points distincts en commun sont dites confondues. Elles ont alors tous leurs points en commun.
Deux droites qui ne sont pas sécantes sont parallèles.
Deux droites qui ont deux points distincts en commun sont dites confondues. Elles ont alors tous leurs points en commun.
Exercices n° p.312-314
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Couples d'angles
Définitions
Deux angles sont adjacents s'ils ont le même sommet, un côté en commun et s'ils sont de part et d'autre de ce côté en commun.
Quand on coupe un angle plat en deux, on obtient deux angles adjacents dont la somme des mesures vaut 180°.
On dit qu'ils sont supplémentaires.
On dit qu'ils sont supplémentaires.
Quand on coupe un angle droit en deux, on obtient deux angles adjacents dont la somme des mesures vaut 90°.
On dit qu'ils sont complémentaires.
On dit qu'ils sont complémentaires.
Exercices n° p. 312-314.
Définition
Soit deux droites d et d^\prime sécantes en un point A. Les angles \color{#c21546}\widehat{\text{A}}_1 et \color{#c21546}\widehat{\text{A}}_3 sont dits opposés par le sommet et {\color{#c21546}\widehat{\text{A}}_1} = {\color{#c21546}\widehat{\text{A}}_3}. De même, les angles \color{#3ca69b}\widehat{\text{A}}_2 et \color{#3ca69b}\widehat{\text{A}}_4 sont opposés par le sommet et {\color{#3ca69b}\widehat{\text{A}}_2} = \color{#3ca69b}\widehat{\text{A}}_4.
Exercices n° p. 312-314.
Définitions
On considère deux droites d_1 et d_2 coupées par une sécante d. Il existe plusieurs couples d'angles remarquables, dont :
- les angles alternes-internes
- les angles correspondants
Exercices n° p. 312-314.
J'applique
Consigne :
Dans la figure suivante, quelle est la nature des angles suivants ?
a. \widehat{\text{ABC}} et \widehat{\text{DBE}}
b. \widehat{\text{DBE}} et \widehat{\text{BEF}}
c. \widehat{\text{DBE}} et \widehat{\text{GEH}}
Dans la figure suivante, quelle est la nature des angles suivants ?
a. \widehat{\text{ABC}} et \widehat{\text{DBE}}
b. \widehat{\text{DBE}} et \widehat{\text{BEF}}
c. \widehat{\text{DBE}} et \widehat{\text{GEH}}
Correction :
a. Les angles \widehat{\text{ABC}} et \widehat{\text{DBE}} sont opposés par le sommet.
b. Les angles \widehat{\text{DBE}} et \widehat{\text{BEF}} sont de part et d'autre de la sécante et à l'intérieur des deux droites. Ils sont donc alternes-internes.
c. Les angles \widehat{\text{DBE}} et \widehat{\text{GEH}} sont du même côté de la sécante. \widehat{\text{DBE}} est à l'intérieur mais \widehat{\text{GEH}} à l'extérieur. Ils sont donc correspondants.
a. Les angles \widehat{\text{ABC}} et \widehat{\text{DBE}} sont opposés par le sommet.
b. Les angles \widehat{\text{DBE}} et \widehat{\text{BEF}} sont de part et d'autre de la sécante et à l'intérieur des deux droites. Ils sont donc alternes-internes.
c. Les angles \widehat{\text{DBE}} et \widehat{\text{GEH}} sont du même côté de la sécante. \widehat{\text{DBE}} est à l'intérieur mais \widehat{\text{GEH}} à l'extérieur. Ils sont donc correspondants.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3 Parallélisme
Propriété
- Si d_1 et d_2 sont parallèles et coupées par d, alors deux angles alternes-internes ou correspondants sont de même mesure.
- Si deux angles alternes-internes ou correspondants sont de même mesure, alors d_1 et d_2 sont parallèles.
- Si deux angles alternes-internes ou correspondants n'ont pas la même mesure, alors d_1 et d_2 ne sont pas parallèles.
Exercices n° p. 312-314.
J'applique
Consigne :
On considère la figure ci-dessous dans laquelle les droites \text{(AB)} et \text{(ED) }sont parallèles. Quelle est la mesure de l'angle \widehat{\text{BCD}} ?
Correction :
Les angles \widehat{\text{EDF}} et \widehat{\text{ACD}} sont correspondants.
Comme les droites (AB) et (ED) sont parallèles, \widehat{\text{EDF}} = \widehat{\text{ACD}} = 45^{\circ}.
Or les angles \widehat{\text{ACD}} et \widehat{\text{BCD}} sont supplémentaires, donc \widehat{\text{ACD}} +~\widehat{\text{BCD}} = 180^{\circ}.
Donc \widehat{\text{BCD}} = 135^{\circ}.
On considère la figure ci-dessous dans laquelle les droites \text{(AB)} et \text{(ED) }sont parallèles. Quelle est la mesure de l'angle \widehat{\text{BCD}} ?
Les angles \widehat{\text{EDF}} et \widehat{\text{ACD}} sont correspondants.
Comme les droites (AB) et (ED) sont parallèles, \widehat{\text{EDF}} = \widehat{\text{ACD}} = 45^{\circ}.
Or les angles \widehat{\text{ACD}} et \widehat{\text{BCD}} sont supplémentaires, donc \widehat{\text{ACD}} +~\widehat{\text{BCD}} = 180^{\circ}.
Donc \widehat{\text{BCD}} = 135^{\circ}.
Consigne :
Les droites \text{(AB)} et \text{(CD)} sont-elles parallèles ?
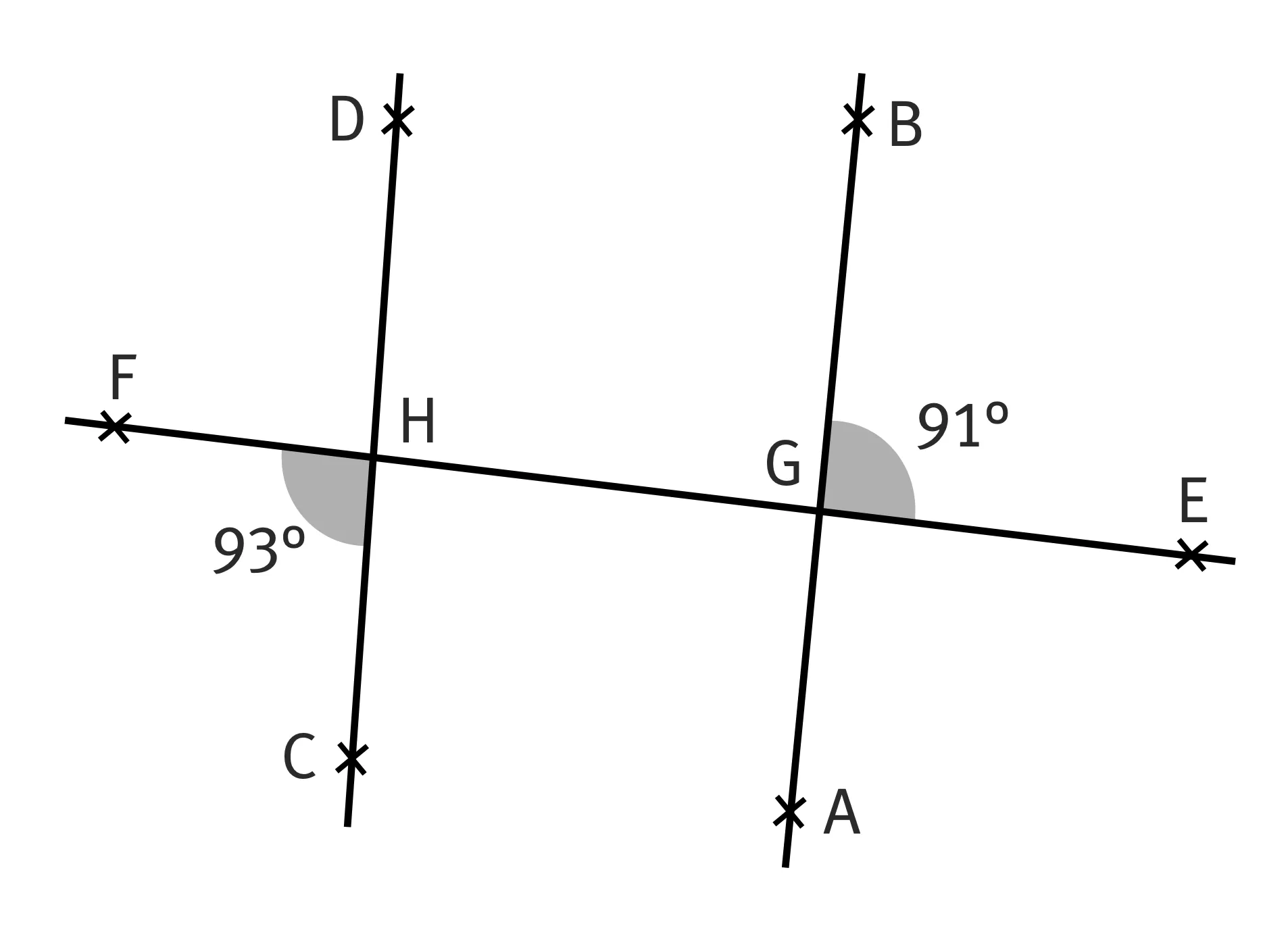Correction :
Les angles \widehat{\text{HGA}} et \widehat{\text{BGE}} sont opposés par le sommet ; ils ont donc la même mesure.
Or les angles \widehat{\text{HGA}} et \widehat{\text{CHF}} sont correspondants et n'ont pas la même mesure. Donc les droites \text{(AB)} et \text{(CD)} ne sont pas parallèles.
Les droites \text{(AB)} et \text{(CD)} sont-elles parallèles ?
Les angles \widehat{\text{HGA}} et \widehat{\text{BGE}} sont opposés par le sommet ; ils ont donc la même mesure.
Or les angles \widehat{\text{HGA}} et \widehat{\text{CHF}} sont correspondants et n'ont pas la même mesure. Donc les droites \text{(AB)} et \text{(CD)} ne sont pas parallèles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BParallélogrammes quelconques
Je découvre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Propriétés des parallélogrammes
Définition
Un parallélogramme ABCD est un quadrilatère dont les côtés opposés sont parallèles deux à deux. Donc (AB) ⁄⁄ (DC) et (AD) ⁄⁄ (BC).
Exercices n° p. 314-315.
Propriétés
Les diagonales d'un parallélogramme se coupent en leur milieu. Ce point est un centre de symétrie du quadrilatère.
Ses côtés opposés sont de même longueur deux à deux.
Exercices n° p. 314-315.
J'applique
Consigne :
On reprend le parallélogramme \text{ABCD} suivant.
On sait que AD = 3 cm et que OB = 2 cm. Quelles sont les valeurs des longueurs des segments :
a. \text{[BC]} ? b. \text{[BD]} ?
Correction :
a. \text{[BC]} est le segment opposé à \text{[AD]}, donc \text{BC} = \text{AD} = 3~\text{cm}.
b. \text{[AC]} et \text{[BD]} se croisent en leur milieu, donc :
\text{BD} = \text{OD} + \text{OB} = 2 \times \text{OB}
\text{BD} = 4 cm.
Remarque :
L'image de A par la symétrie de centre O est C ; l'image de B par cette même symétrie est D.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Caractérisations des parallélogramme
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CParallélogrammes particuliers
Je découvre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Quelques parallélogrammes particuliers
Rappel
Les carrés, les losanges et les rectangles sont des parallélogrammes. Toutes les propriétés des parallélogrammes s'appliquent à eux, mais ils en possèdent d'autres qui leur sont propres.
- Rectangle : Tous ses angles sont droits et ses diagonales sont de même longueur.
- Losange : Ses diagonales sont perpendiculaires et tous ses côtés sont de même longueur.
- Carré : C'est un parallélogramme particulier qui est à la fois un rectangle et un losange.
Exercices n° p. 315-317.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Reconnaitre un parallélogramme particulier.
Méthodes
- Un parallélogramme ayant un angle droit ou des diagonales de même longueur est un rectangle.
- Un parallélogramme ayant deux côtés consécutifs de même longueur ou des diagonales perpendiculaires est un losange.
Exercices n° p. 315-317.
J'applique
Consigne :
Le quadrilatère \text{ABCD} suivant est-il un quadrilatère particulier ?
- \text{ABCD} est-il un parallélogramme ?
On remarque que \text{AB = CD} et que \text{AD = BC}. Les côtés opposés sont donc de même longueur.
\text{ABCD} est donc un parallélogramme. - \text{ABCD} est-il un rectangle ?
L'angle \widehat{\text{DAB}} vaut 124°. Il n'est donc pas droit. \text{ABCD} n'est donc pas un rectangle - \text{ABCD} est-il un losange ?
L'angle entre les diagonales \text{[AC]} et \text{[DB]} vaut 93°. Ses diagonales ne sont pas perpendiculaires. \text{ABCD} n'est donc pas un losange.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
