Nos classiques

Mathématiques Cycle 4

Mes Pages
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Ch. 7
Puissances
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et géométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Théorème de Pythagore
Ouverturep. 347
Je découvre le chapitre
Introductionp. 348-349
J'apprends
Coursp. 350-352
Questions Flash / Je m'entraine
Exercicesp. 353-357
Problèmes résolus
Problèmesp. 358
Problèmes résolus
Problèmesp. 359
Je résous des problèmes
Exercicesp. 360-363
Exercices numériques
Exercicesp. 364
Maths autrement : Les secrets de racine carrée de 2
Travailler autrementp. 365
Je m'évalue
Exercicesp. 366
Ch. 17
Agrandissements - réductions
Ch. 18
Trigonométrie
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Nos dossiers d'actualité
Dossier d'actualité
Chapitre 16
Exercices

Questions Flash - Je m'entraine

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Questions flash

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1. Quelles sont les affirmations correctes ?
Triangle ABC rectangle en C





2. Le théorème de Pythagore dans un triangle ABC rectangle en A sʼécrit :




3. ABCD est un carré de côté 5 cm.





4. Si AB = 3 cm, AC = 4 cm et BC = 5 cm, alors le triangle ABC...





5. ABCD est un rectangle de longueur 5 cm et de largeur 4 cm. Lʼarrondi au dixième de AC est...
ABCD est un rectangle de longueur 5 cm et de largeur 4 cm. Lʼarrondi au dixième de AC est...





6. La racine carrée de 16 est...





7. Lʼarrondi au dixième de la racine carrée de 29 est...





8. Un encadrement de la racine carrée de 35 est...



Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Je m'entraine

Utilisation du théorème
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1
Triangles.

1. Quels sont les côtés appelés « hypoténuse » ? Quels sont les côtés adjacents à lʼangle droit ?
Triangle RTS rectangle en T
2. Quels sont les côtés appelés « hypoténuse » ? Quels sont les côtés adjacents à lʼangle droit ?
Triangle KLM rectangle en L
3. Quels sont les côtés appelés « hypoténuse » ? Quels sont les côtés adjacents à lʼangle droit ?
Triangle ACB rectangle en C
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

4
Égalité de Pythagore.

Quadrilatère formé de plusieurs triangles dont 3 triangles rectangles
1. Écrivez lʼégalité de Pythagore pour chacun des triangles rectangles suivants.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

2
Triangles rectangles.

Quadrilatère formé de plusieurs triangles dont 3 triangles rectangles
1. Dans chacun des triangles rectangles de la figure, quels sont les côtés appelés hypothénuse ? Quels sont les côtés adjacents à l'angle droit ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

3
Égalité de Pythagore.

✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème

Graphique lié à l'exercice 7
Graphique lié à l'exercice 8
1. Écrivez lʼégalité de Pythagore pour les triangles ABC et DEF respectivement rectangles en A et D.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

5
DEF est un triangle rectangle avec EF = 5 cm et DF = 5,6 cm.

1. Quelles peuvent être les mesures du côté [ED] ?
2. En quel angle DEF est-il rectangle dans chacun de ces cas ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Racine carrée
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

6
Calcul mental.

1. Complétez.

x 5 7 1
12
x^2
16 49
100
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

7
Calcul mental.

1. Complétez.

x 1 25 64 121 16 49
\sqrt{x}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

8
Calcul mental.

1. Complétez.

x 8 0,1
25 10 000
x^2
0,64
10 000 000
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

9
À l'aide de la calculatrice.

1. Complétez en arrondissant au dixième.

x 10 6 11 50 24 82
\sqrt{x}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

10
Sans utiliser la calculatrice, donnez la valeur des racines carrés suivantes.

✔ J'utilise l'écriture d'un nombre la plus appropriée pour calculer

1. \sqrt{25}
2. \sqrt{144}
3. \sqrt{81}
4. \sqrt{49}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Calcul de longueurs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

11
Le triangle EFG est rectangle en F, EF = 2,5 cm et EG = 4 cm.

✔ Je décompose un problème en sous-problèmes pour le simplifier et le résoudre

Triangle EFG rectangle en F
1. Calculez lʼaire du triangle rectangle EFG. On cherche une valeur arrondie au centième.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

12
Le triangle STU est rectangle en S tel que ST = 8 cm et SU = 6 cm.

1. Calculez TU^{2}, le carré de la longueur de l'hypoténuse. Déduisez-en la longueur de l'hypoténuse.
2. Construisez le triangle STU et mesurez la longueur du côté [TU].

Logo Geogebra

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

3. Comparez la longueur mesurée avec la longueur obtenue par le calcul.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

13
Le triangle IJK est rectangle en J. IJ = 20 cm et JK = 13 cm.

1. Calculez la longueur de l'hypoténuse arrondie au mm.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

14
Le triangle ZOE est rectangle en Z tel que ZO = 2,8 cm et ZE = 9,6 cm.

1. Calculez OE^{2}, le carré de la longueur de l'hypoténuse. Déduisez-en la longueur de l'hypoténuse.
2. Construisez le triangle ZOE et mesurez la longueur du côté [OE].

Logo Geogebra

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

3. Comparez la longueur mesurée avec la longueur obtenue par le calcul.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

15
Le triangle RST est rectangle en R. ST = 11 cm et RS = 7 cm.

1. Calculez la longueur du troisième côté arrondie au mm.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

16
Savoir refaire
À quelle hauteur lʼéchelle touche-t-elle le mur ?

✔ Je modélise une situation à l'aide d'un schéma, d'un tableau ou d'un arbre

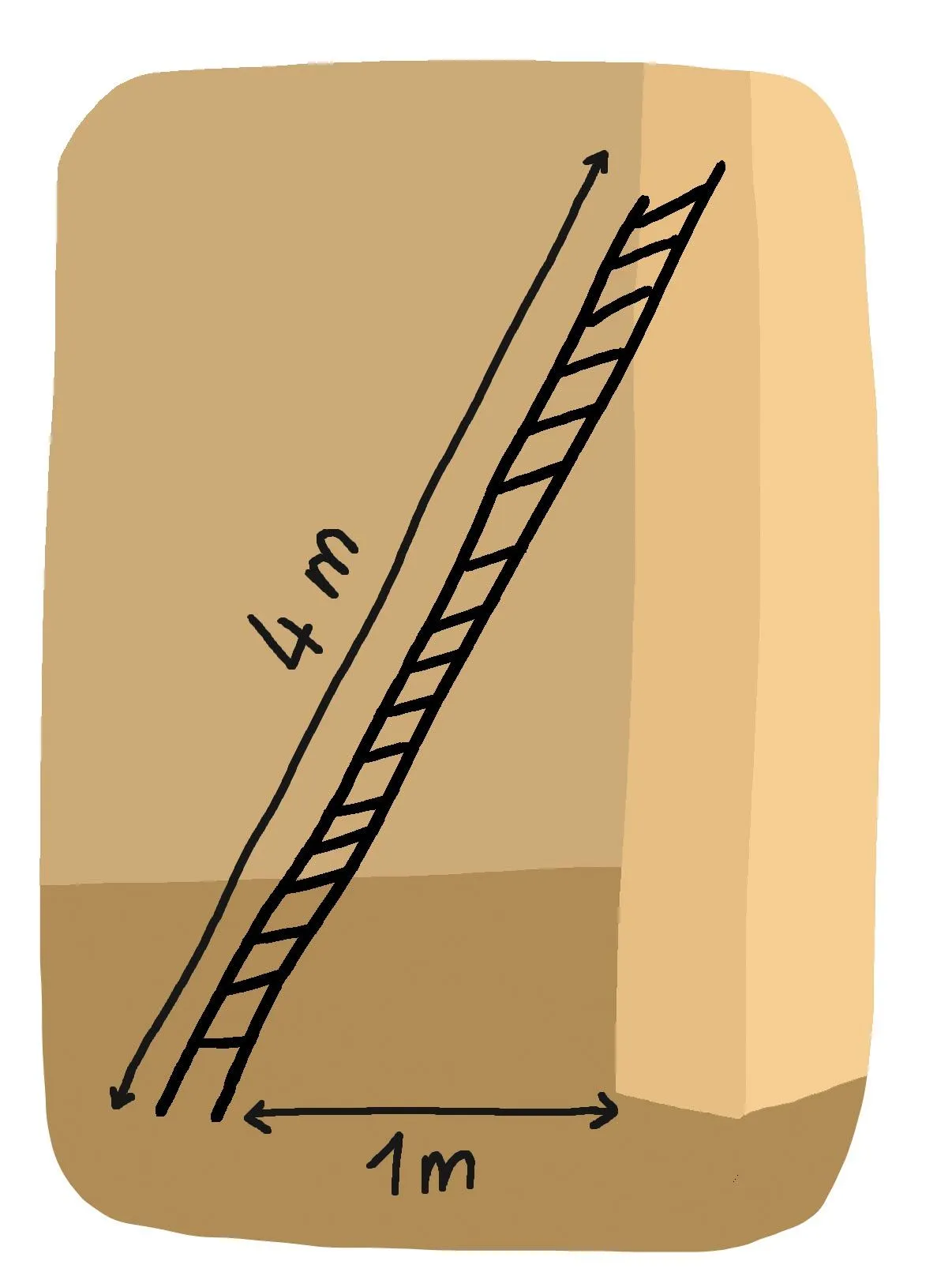Placeholder pour Schéma : échelle de 4 m appuyée contre un mur, son pied étant à 1 m du mur.Schéma : échelle de 4 m appuyée contre un mur, son pied étant à 1 m du mur.
1. Donnez un arrondi au cm.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

17
Le triangle EFG est rectangle en F tel que EG = 8,5 cm et FG = 7,5 cm.

1. Calculez la longueur du côté [EF].
2. Construisez le triangle EFG et mesurez la longueur du côté [EF].

Logo Geogebra

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

3. Comparez la longueur mesurée avec la longueur obtenue par le calcul.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

18
Le triangle KLM est rectangle en M.

Calculez la longueur du troisième côté arrondie au centième

1. KM = 6 cm et LM = 5 cm
2. KM = 20 cm et LM = 15 cm
3. KM = 2,5 m et LM = 3 m

4. KM = 1 m et LM = 2 m
5. KM = 6 m et LM = 250 m
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

19
Longueur du côté d'un triangle.

✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème

1. Calculez la longueur du troisième côté.
Triangle ABC rectangle en C, BC=6cm, BA=9cm

2. Calculez la longueur du troisième côté.
Triangle ABC rectangle en B, BC=7cm, BA=5cm

3. Calculez la longueur du troisième côté.
Triangle ABC rectangle en B, AC=11cm, BA=9cm
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

20
Triangle.

Graphique lié à l'exercice 15
1. Calculez lʼarrondi au dixième de la longueur de la hauteur relative au côté [AB] du triangle ABC.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

21
Triangle.

Graphique lié à l'exercice 16
1. Dans un triangle isocèle DEF, la hauteur issue de F mesure 7 cm. Calculez l'arrondi au mm de la longueur du côté [EF].
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

22
Savoir refaire
Diagonale d'un rectangle.

✔ Je choisis un cadre adapté (numérique, algébrique ou géométrique) pour traiter un problème

1. Calculez lʼarrondi au mm de la longueur de la diagonale dʼun rectangle de longueur 10 cm et de largeur 15 cm.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

23
Diagonale d'un carré.

1. Exprimez la longueur de la diagonale d dʼun carré de côté a à lʼaide dʼune formule.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

24
Un rectangle a une aire de 74 cm^{ 2} et sa longueur mesure 14,8 cm.

1. Calculez sa largeur.
2. Déterminez la longueur de ses diagonales.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

25
Savoir refaire
Losange.

✔ Je structure mon raisonnement

Losange IJKL, les diagonales LJ=8cm et Ik=6cm se croisent en O.
1. Calculez la longueur du côté du losange IJKL dont les deux diagonales mesurent 6 cm et 8 cm.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

26
Cerf-volant.

Losange ABCD, AC et DB se croisent perpendiculairement
Dans le quadrilatère ABCD, on connait la longueur des diagonales AC = 70 cm et BD = 1 m.

1. Calculez la longueur des côtés de ce quadrilatère.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

27
La figure représente un cercle de centre O dont on ignore le rayon.

Cerle de centre O dont on ignore le rayon
La corde [AB] mesure 8 cm, le segment [IP] mesure 2cm et BM = 4\sqrt{ 5} .

1. Déterminez le rayon du cercle sachant que IBM est un triangle rectangle.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

28
Aux forces unies des théorèmes.

Triangles ADC coupé par PA et EB
Dans la figure :
  • AB = 5 cm ;
  • BI = 3 cm ;
  • PI = 1 cm ;
  • BE = 4,5 cm ;
  • PC = 3,75 cm ;
  • DE = 1,1 cm.

1. Calculez les longueurs EI ; AI ; AE ; AC ; DP et CD. Donnez des valeurs approchées au dixième.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

29
Le quadrilatère ABCD est rectangle en C.

✔ Je structure mon raisonnement

Quadrilatère ABCD rectangle en C, AB est coupé en N et DA est coupé en M.
On sait que :
  • ABCD est symétrique par rapport à l'axe (AC) ;
  • AB = AC = 6 cm ; BC = DC = 4 cm ;
  • M est le milieu du côté [AD] ;
  • N est le milieu du côté [AB].

1. Calculez DB.
2. (CA) coupe [DB] perpendiculairement en son milieu, I. Combien vaut AI ?
3. [AI] et [MN] se coupent en leur milieu P. Combien valent AP et AM ?
4. Calculez PM et MN.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

30
Dans un parallélépipède rectangle.

✔ Je modélise une situation à l'aide d'un schéma, d'un tableau ou d'un arbre

1. Quelle est la longueur du plus long segment à lʼintérieur dʼun parallélépipède rectangle dʼarêtes 3 cm, 4 cm et 5 cm ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Reconnaitre un triangle rectangle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

31
Construisez les triangles ABC suivants.

✔ J'envisage plusieurs méthodes de résolution

1. Construisez le triangle a. : AB = 10 cm, AC= 6 cm et BC = 8 cm.

Logo Geogebra

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

2. Construisez le triangle b. AB = 7 cm, AC = 3 cm et BC = 6 cm.

Logo Geogebra

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

32
Les triangles ABC sont-ils rectangles ? Justifiez vos réponses.

1. AB = 0,7 cm, AC = 2,4 cm et BC = 2,5 cm
2. AB = 12 cm, AC = 12 cm et BC = 18 cm
3. AB = 7 cm, AC = 33 cm et BC = 40 cm
4. AB = 33 m, AC = 56 m et BC = 65 m
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

33
Les triangles EFG sont-ils rectangles ? Justifiez vos réponses.

1. EF = 7 cm, EG = 2,4 cm et FG = 7,4 cm
2. EF = 27 cm, EG = 120 cm et FG = 123 cm
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

34
Parallélogramme.

1. Un parallélogramme ABCD tel que AB = 31 cm, BC = 48 cm et AC = 65 cm est-il un rectangle ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

35
Parallélogramme

1. Un parallélogramme ABCD tel que AB = 31 cm, BC = 31 cm et AC = 43 cm est-il un carré ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

36
Quadrilatère.

✔ Je représente des objets et des fissures géométriques

Quadrilatère LMOE composé de deux triangles MOE et ELM
Voici la figure à main levée dʼun quadrilatère. Le triangle OEM est isocèle en O et ME = 5,6 cm. Le triangle LEM est isocèle en L et LM = 4 cm.

1. Reproduisez la figure en grandeur réelle.

Logo Geogebra

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

2. Démontrez que OELM est un cerf-volant.
Coup de pouce
Pensez aux caractéristiques des hauteurs des triangles ísocèles.

3. OELM est-il un carré ?
Coup de pouce
Pensez aux caractéristiques des diagonales d'un carré.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

37
Un grand triangle

1. Un triangle dont les côtés mesurent 1 028 cm, 1 782 cm et 2 010 cm est-il rectangle ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

38
Dans la figure, on sait que les points A, O et B dʼune part et C, O et D dʼautre part sont alignés.

✔ Je reconnais une situation de proportionnalité

Figure ABDC en forme de sablier les bords se croisent en o
  • AC = 9 cm,
  • OC = 12 cm,
  • OA = 15 cm,
  • OB = 5 cm,
  • DB = 4 cm,
  • OD = 3 cm.

1. Les droites (AB) et (CD) sont-elles perpendiculaires ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

A
Exercice numérique

Soit A B C un triangle rectangle en A tel que AB= 5 cm et BC= 12 cm.

1. Construire le triangle A B C en vraie grandeur.

2. Déterminer la valeur exacte de la longueur AC.

3. Vérifier le résultat sur la figure.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

B
Exercice numérique

Soit A B C un triangle rectangle en A tel que AB= 10 cm et AC= 11 cm. 1. Construire le triangle A B C en vraie grandeur.

2. Déterminer la valeur exacte de la longueur BC.

3. Vérifier le résultat sur la figure.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Parcours de compétences

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Énoncé

✔ Je participe à une recherche collective de résolution de problème.

Yasmine et son cousin Mattéo font une balade en rase campagne. Ils admirent le paysage devant eux.« – Comme la Terre est ronde, il y a un moment où une partie de la Terre est cachée, remarque Mattéo. Crois-tu que l'on pourrait préciser où se situe cet endroit géographiquement ?– Facile, lui répond Yasmine, je mesure 1,70 m... Remarque, si on grimpait au 3e étage de la tour Eiffel, cet endroit se trouverait dix fois plus loin... »

Que pensez-vous de lʼaffirmation de Yasmine ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Niveau 1

J'écoute les autres

Coup de pouce
Quelles solutions sont proposées par vos camarades ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Niveau 2

Je donne mon avis quand on le demande.

Coup de pouce
Répondez aux questions des autres ou du professeur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Niveau 3

Je propose une méthode de résolution au groupe.

Coup de pouce
Si vous étiez seul pour réoudre ce problème, comment feriez-vous ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Niveau 4

J'anime le débat et je participe à l'élaboration de la réponse.

Coup de pouce
Posez des questions aux autres et prenez en compte leurs réponses pour améliorer la méthode.

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.