Nous allons utiliser un algorithme pour comprendre comment évoluent les probabilités de chaque issue quand lʼenvironnement dans lequel se situe un évènement évolue.

1. Douze cafards fous organisent une course. Elle se déroule comme suit. Chaque cafard porte un numéro. Ils choisissent ensuite un nombre au hasard, compris entre 1 et 12. Le cafard qui porte pour numéro le nombre choisi avance dʼun pas. Puis ils recommencent jusquʼà ce que lʼun dʼentre eux passe la ligne dʼarrivée. Ouvrez le fichier Scratch de lʼexercice.
a. Ouvrez le fichier Scratch de l'exercice. Dans la scène, modifiez le script du lutin afin que la course se déroule selon la règle établie par les cafards.

b. Est-il vrai que si lʼon fait 12 courses, chaque cafard gagnera une fois ?

2. Les douze cafards changent de règle. Dorénavant, ils choisiront deux nombres au hasard compris entre 1 et 6. Le cafard qui porte pour numéro la somme des deux nombres choisis avance dʼun pas. Puis ils recommencent jusquʼà ce que lʼun dʼentre eux passe à la ligne dʼarrivée.
a. Choisissez deux nombres au hasard entre 1 et 6 et calculez leur somme.

b. Le cafard numéro 1 déclare forfait. Pourquoi ? Comment se nomme lʼévènement « Le cafard 1 gagne la course » ?

c. Dans la scène, modifiez le script du lutin afin que la course se déroule selon la règle établie par les cafards.

d. Les onze cafards restants ont-ils la même chance de gagner ? Sauriez-vous expliquer pourquoi ?

3. Saurez-vous trouver une règle du jeu qui fasse que ce soit le cafard numéro 8 qui ait plus de chance de gagner que les autres ? (Ne choisir que le nombre 8 ne compte pas comme une règle valide : les autres cafards déclareraient forfait !)

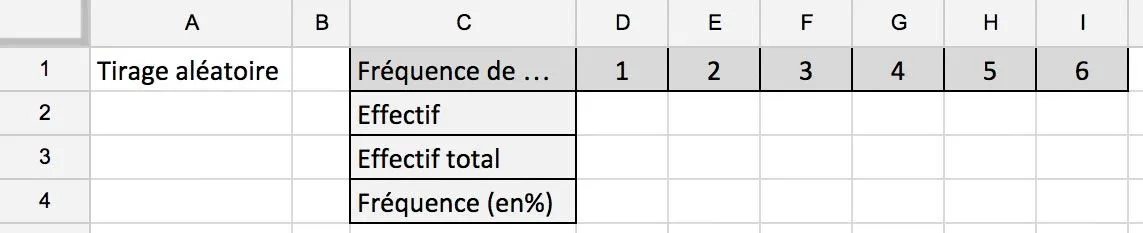
Nous allons simuler et étudier des probabilités à lʼaide dʼun tableur en travaillant sur la fréquence dʼapparition de chaque face dʼun dé.Créez un nouveau document tableur et recopiez les cases du tableau ci-contre.