Exercices numériques

Exercice 43 : Tableur : Forme d'une pyramide en fonction de la forme de sa base

Nous allons étudier à lʼaide dʼun tableur le nombre de faces, de sommets et dʼarêtes dʼune pyramide en fonction du nombre de côtés de sa base.Téléchargez le fichier ressource de l'exercice.

1

Combien une pyramide dont la base est en forme de quadrilatère a-t-elle de faces ? De sommets ? Dʼarêtes ?

2

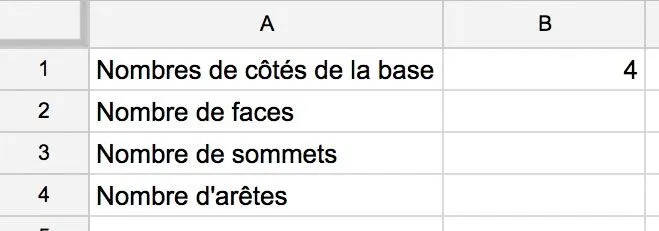
En vous basant sur l'image ci-contre, quelle formule doit-on mettre dans les cellules B2, B3 et B4 ?

3

Ouvrez le fichier tableur joint ou recopiez dans un tableur le tableau et testez vos formules. Vérifiez vos réponses à la question précédente.

4

Modifiez la cellule B1 pour avoir une pyramide à base hexagonale. Combien a-t-elle de faces ? De sommets ? Dʼarêtes ?

Exercice 44 : Logiciels de géométrie dynamique : Sphère et boule

Ouvrez un logiciel de géométrie dynamique en mode « graphique 3D ».

1

Tracez une sphère de centre O et de rayon 4 cm.

2

Placez deux points M et N sur cette sphère tels que M et N soient diamétralement opposés.

3

Combien mesure [MN] ? Pourquoi ?

4

Vérifiez cette longueur à lʼaide du logiciel.

Exercice 45 : Scratch : Construction d'un pavé droit

Nous allons construire un pavé droit de dimensions 100 pas × 60 pas × 50 pas en perspective à lʼaide du logiciel Scratch. Ouvrez le document Scratch de lʼexercice.

1

Testez ce programme.

2

On ne veut plus quʼil y ait dʼespace entre les « couches » qui forment ce pavé. Complétez le programme.

3

Modifiez ce programme pour tracer un cube de 60 pas de côté.

Exercice 46 : Logiciel de géométrie dynamique : Section d'une pyramide

Nous allons tracer une pyramide et le plan qui la sectionne à lʼaide dʼun logiciel de géométrie dynamique.

1

Placez les points A (−2 ; 0), B (3 ; 0), C (3 ; 3) et D (−2 ; 3). Tracez le polygone ABCD.

2

Ouvrez lʼaffichage « graphique 3D ». En utilisant lʼicône « extrusion », tracez la pyramide de base ABCD, de sommet E et de hauteur 7 cm.

3

Placez un point F sur [AE] tel que AF = 5 cm. Tracez un plan parallèle à la base ABCD passant par F. Quelle est la nature de la section formée ? Vérifiez que les longueurs des côtés de la section sont proportionnelles à la base ABCD.