Chapitre 15
Exercices
Je résous des problèmes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25Un beau paquet cadeau
Le cadeau de Virginie est de forme cubique. Il est empaqueté dans du papier rouge. Deux rubans verts lʼentourent en joignant le milieu des arêtes.
Représentez le cadeau et les rubans en perspective cavalière, puis dessinez un patron de ce cube et indiquez-y lʼendroit où passent les rubans.
Représentez le cadeau et les rubans en perspective cavalière, puis dessinez un patron de ce cube et indiquez-y lʼendroit où passent les rubans.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26Savoir refaireCoupe d'un pavé droit

1. Que peut-on dire de \text{(IJ)} et \text{(AB)} ?
2. Le point \text{K} de \text{[FG]} est tel que \text{FK = 3,5 cm}. Le plan passant par \text{I}, \text{J} et \text{K} coupe \text{[EH]} en \text{L}. Déterminez la nature de la section plane de \text{ABCDEFGH} par ce plan. Donnez les dimensions de la section plane.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27Camion citerne

1. Déterminez la capacité maximale de la citerne.
2. La citerne est remplie partiellement : le niveau dʼeau est à \text{20 cm} en dessous de la moitié du réservoir. Quelle est la forme de la surface de lʼeau ?
3. Déterminez les dimensions de cette surface.
4. Déterminez lʼaire de cette surface en \mathrm{m}^{2}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28Savoir refaireChâteau d'eau

\mathrm{AH}=\mathrm{AO}=11,4 \mathrm{~m}.
1. Déterminez le volume de la citerne au \mathrm{dm}^{3} près.
2. Combien de litres dʼeau faut-il pour remplir la citerne à moitié ?
3. Quelle part de la contenance totale un remplissage au niveau de la ligne rouge représente-t-il ?
1. Déterminez le volume de la citerne au \mathrm{dm}^{3} près.
2. Combien de litres dʼeau faut-il pour remplir la citerne à moitié ?
3. Quelle part de la contenance totale un remplissage au niveau de la ligne rouge représente-t-il ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29Vers le Brevet (Polynésie, 2011)
1. La section \text{AIJD} du cube est-elle un losange, un rectangle, un parallélogramme ou un carré ?

2. Dessinez en grandeur réelle le triangle \text{AIB} et la section \text{AIJD}.
3. Montrez que lʼaire du triangle \text{AIB} est égale à 9 \mathrm{~cm}^{2}.
4. La partie basse \text{ABCDJI} du cube est un prisme droit. Calculez le volume du prisme droit \text{ABCDJI} en \mathrm{cm}^{3}.
3. Montrez que lʼaire du triangle \text{AIB} est égale à 9 \mathrm{~cm}^{2}.
4. La partie basse \text{ABCDJI} du cube est un prisme droit. Calculez le volume du prisme droit \text{ABCDJI} en \mathrm{cm}^{3}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30Savoir refaireDans un aquarium
Un aquarium en forme de sphère coupée de 15 \mathrm{~cm} de rayon est rempli d'eau à une hauteur de 21 \mathrm{~cm}.

1. Quelle forme a la surface de lʼeau ? Quelle est lʼaire en \mathrm{cm}^{2} de cette surface ?
2. Le niveau dʼeau baisse jusquʼà atteindre le point \text{O}. Quel volume dʼeau en \mathrm{cm}^{3} reste-t-il dans le bocal ?
2. Le niveau dʼeau baisse jusquʼà atteindre le point \text{O}. Quel volume dʼeau en \mathrm{cm}^{3} reste-t-il dans le bocal ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31Un jeu finlandais
Marc, Pierre et Romain jouent à un jeu de quilles un peu spécial. Ce jeu se joue avec des quilles en bois. Les quilles sont obtenues par la section en biais dʼun cylindre en bois.
1. Construisez une représentation cavalière dʼune quille.
1. Construisez une représentation cavalière dʼune quille.
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32Coupe d'une sphère
S est une sphère de centre \text{O}. On la coupe par un plan passant par \text{O'} tel que \text{OO' = 4 cm}. \text{M} est un point de cette section tel que le triangle \text{OO'M} est rectangle isocèle en \text{O'}.
 1. Quel est le rayon de la sphère S ?
1. Quel est le rayon de la sphère S ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33La Géode
La Géode est une salle de cinéma à Paris permettant de projeter des films à 360^{\circ}. Cette salle a la forme dʼune sphère de \text{36 m} de diamètre, avec une section à sa base. Lorsque lʼon est à lʼintérieur de la Géode, le plafond se trouve \text{29 m} au-dessus de notre tête.
 1. Quelle est la surface au sol de la Géode ?
1. Quelle est la surface au sol de la Géode ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
34De l'autre côté du monde
Les coordonnées géographiques de la ville de Syracuse en Italie sont approximativement de 37^{\circ}~\mathrm{N} et 15^{\circ}~\mathrm{E}.
1. Déterminez les coordonnées géographiques du point situé diamétralement à lʼopposé de Syracuse.
2. Où se situe approximativement ce point ?
1. Déterminez les coordonnées géographiques du point situé diamétralement à lʼopposé de Syracuse.
2. Où se situe approximativement ce point ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35Distances terrestres
Sachant que la Terre a un rayon de {6~371 \mathrm{~km}}. Quelle est la distance du Sud à lʼOuest...
1. en ligne droite, à lʼintérieur de la Terre ?
2. à vol dʼoiseau en suivant la surface de la Terre ?
1. en ligne droite, à lʼintérieur de la Terre ?
2. à vol dʼoiseau en suivant la surface de la Terre ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
36Méridiens et parallèles



2. Quelle est la longueur de lʼÉquateur ?
3. Quelle est la longueur dʼun méridien ?
4. Quelles sont les coordonnées du pôle Nord ? Du pôle Sud ? Dʼune ville située sur lʼÉquateur ? De la ville de Greenwich ?
5. Le plus court chemin pour aller du point de coordonnées {22^{\circ}~\mathrm{S}}, {43^{\circ}~\mathrm{O}} au point {10^{\circ}~\mathrm{N}}, {106^{\circ}~\mathrm{E}} passe-t-il par lʼÉquateur ? Par le méridien de Greenwich ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
37À la surface de la Terre
On considère les villes de Santiago du Chili (\text{S}), Boston (\text{B}) et Carcassonne (\text{C}). Leurs coordonnées géographiques sont :
{\mathrm{S}\left(33^{\circ}~\mathrm{S}~; 70^{\circ}~\mathrm{O}\right)} ;
{\mathrm{B}\left(43^{\circ}~\mathrm{N}~; 70^{\circ}~\mathrm{O}\right)} ;
{\mathrm{C}\left(43^{\circ}~\mathrm{N}~; 2^{\circ}~\mathrm{E}\right)}.
1. Que peut-on dire des villes Santiago du Chili et Boston ?
2. \text{O} est le centre de la Terre. Quelle est la mesure de l'angle \widehat{\text{SOB}} ?
3. Sachant que le rayon de la Terre est de {\text{6~371 km}}, calculez une valeur arrondie au \text{km} près de la distance entre Santiago du Chili et Boston.
4. Reprennez les questions précédentes avec Boston et Carcassonne.
{\mathrm{S}\left(33^{\circ}~\mathrm{S}~; 70^{\circ}~\mathrm{O}\right)} ;
{\mathrm{B}\left(43^{\circ}~\mathrm{N}~; 70^{\circ}~\mathrm{O}\right)} ;
{\mathrm{C}\left(43^{\circ}~\mathrm{N}~; 2^{\circ}~\mathrm{E}\right)}.
1. Que peut-on dire des villes Santiago du Chili et Boston ?
2. \text{O} est le centre de la Terre. Quelle est la mesure de l'angle \widehat{\text{SOB}} ?
3. Sachant que le rayon de la Terre est de {\text{6~371 km}}, calculez une valeur arrondie au \text{km} près de la distance entre Santiago du Chili et Boston.
4. Reprennez les questions précédentes avec Boston et Carcassonne.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
38De Cape Town à Sydney
On considère les villes de Cape Town {\left(33^{\circ}~\mathrm{S}~; 18^{\circ}~\mathrm{E})\right.} et de Sydney {\left(33^{\circ}~\mathrm{S}~; 151^{\circ}~\mathrm{E})\right.}. Le rayon de la Terre est de \text{6~371 km}.
1. Quel est le rayon du parallèle situé {33^{\circ}~ \mathrm{S}} ?
2. Quelle est la distance à vol dʼoiseau entre ces deux villes au \text{km} près ?
1. Quel est le rayon du parallèle situé {33^{\circ}~ \mathrm{S}} ?
Coup de pouce
Le rayon forme un angle droit avec l'axe de rotation de la Terre. On peut utiliser la trigonométrie.
2. Quelle est la distance à vol dʼoiseau entre ces deux villes au \text{km} près ?
Coup de pouce
Il faut d'abord trouver l'angle entre ces deux villes qui ont pour sommet le centre de la sphère.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
39Cartes avec courbes de niveau et randonnées
Pour mieux se repérer sur une carte et pouvoir représenter des montagnes en deux dimensions, il existe une solution : les courbes de niveau.

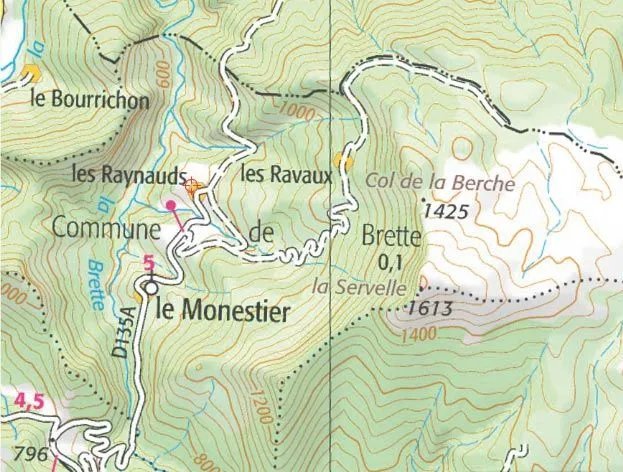 Il suffit de sʼimaginer que lʼon coupe en tranches le relief du paysage. Une personne qui se déplace du point \text{A} au point \text{B} descend de \text{50 m}. Une personne qui se déplace du point \text{B} au point \text{C} monte de \text{100 m}.
Il suffit de sʼimaginer que lʼon coupe en tranches le relief du paysage. Une personne qui se déplace du point \text{A} au point \text{B} descend de \text{50 m}. Une personne qui se déplace du point \text{B} au point \text{C} monte de \text{100 m}.
 Pour représenter cela sur une carte, il suffit de symboliser avec des courbes tous les endroits de la carte ayant la même altitude.
Pour représenter cela sur une carte, il suffit de symboliser avec des courbes tous les endroits de la carte ayant la même altitude.
1. Sur la carte, quel est le point le plus haut représenté ?
2. La ville de Le Monestier se trouve-t-elle à plus de {\text{1~000 m}} dʼaltitude ? À moins de {\text{600 m}} ? À moins de {\text{800 m}} ?
3. Combien y a-t-il de courbes de niveau entre {\text{1~200 m}} et {\text{1~400 m}} dʼaltitude ? Quelle différence dʼaltitude y a-t-il entre deux courbes de niveaux ?



1. Sur la carte, quel est le point le plus haut représenté ?
2. La ville de Le Monestier se trouve-t-elle à plus de {\text{1~000 m}} dʼaltitude ? À moins de {\text{600 m}} ? À moins de {\text{800 m}} ?
3. Combien y a-t-il de courbes de niveau entre {\text{1~200 m}} et {\text{1~400 m}} dʼaltitude ? Quelle différence dʼaltitude y a-t-il entre deux courbes de niveaux ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
40Londres



Coup de pouce
LPC est un triangle rectangle en P.
2. Calculez la mesure de lʼangle \widehat{\text{PCL}} et arrondissez-le au degré près.
Coup de pouce
On peut utiliser la trigonométrie.
3. Déduisez-en, au degré près, la latitude Nord de Londres par rapport à lʼéquateur, cʼest-à-dire l'angle \widehat{\text{LCM}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
41Vers le Brevet (Métropole, 2002)
La Terre est assimilée à une sphère de rayon {\text{6~371 km}}.
 1. On considère le plan perpendiculaire à la ligne des pôles \text{(NS)} et équidistant de ces deux pôles. Lʼintersection de ce plan avec la Terre sʼappelle lʼéquateur. Calculez la longueur de lʼéquateur.
1. On considère le plan perpendiculaire à la ligne des pôles \text{(NS)} et équidistant de ces deux pôles. Lʼintersection de ce plan avec la Terre sʼappelle lʼéquateur. Calculez la longueur de lʼéquateur.
2. On note \text{C} le centre de la Terre et \text{G} un point de lʼéquateur. On considère deux points \text{A} et \text{B} situés en Afrique sur lʼéquateur. Ces points sont disposés comme l'indique le schéma. On sait que {\widehat{\text{GCA}}=42^{\circ}} et {\widehat{\text{GCB}}=9^{\circ}}. Calculez la longueur de l'arc \text{AB}, portion de l'équateur située en Afrique.

2. On note \text{C} le centre de la Terre et \text{G} un point de lʼéquateur. On considère deux points \text{A} et \text{B} situés en Afrique sur lʼéquateur. Ces points sont disposés comme l'indique le schéma. On sait que {\widehat{\text{GCA}}=42^{\circ}} et {\widehat{\text{GCB}}=9^{\circ}}. Calculez la longueur de l'arc \text{AB}, portion de l'équateur située en Afrique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
42L'aquarium de Margaux
Margaux possède un aquarium. Elle le soulève pour changer lʼeau. Avant que Margaux ne vide lʼaquarium, un canard en plastique flottait en plein milieu de la surface de lʼeau.



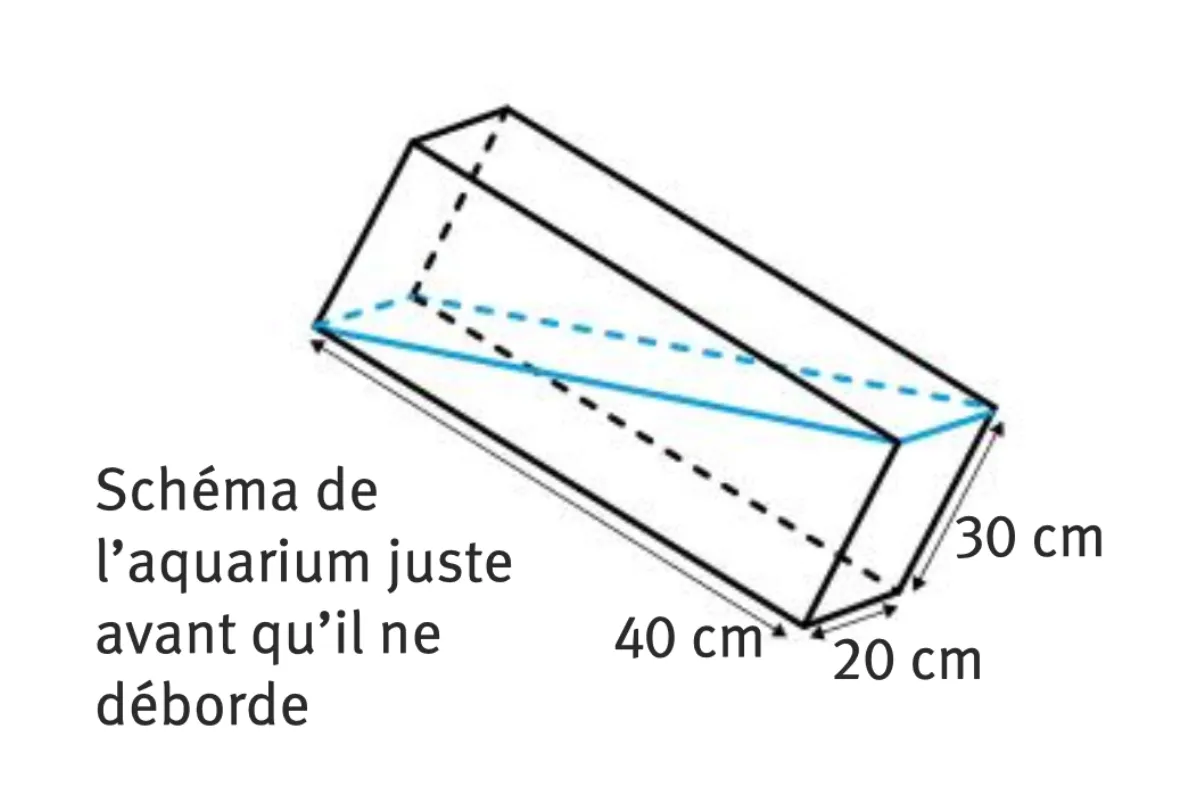 1. Quelles étaient ses coordonnées dans lʼaquarium ?
1. Quelles étaient ses coordonnées dans lʼaquarium ?




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
A Exercice numérique
Jeanne dispose d'un moule en silicone composé de \text{6} cubes de \text{5~cm} de côté ainsi que de \text{5~L} de pâte à gâteaux qu'elle veut utiliser.
1. Combien de fournées va-t-elle devoir réaliser ?
1. Combien de fournées va-t-elle devoir réaliser ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
B Exercice numérique
On dispose d'une citerne de lait de forme cylindrique de \text{80~cm} de diamètre et d'une capacité de \text{800~L}.
1. Déterminer la hauteur de cette citerne.
1. Déterminer la hauteur de cette citerne.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Tâche complexeUn sacré périple !
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Lucile sʼest fait plein dʼamis à lʼuniversité et décide de leur rendre visite pendant ses vacances. Elle veut savoir combien de kilomètres elle a parcouru. Elle fait la liste de ses déplacements.
1. Quelle distance a-t-elle parcourue à votre avis ?
1. Quelle distance a-t-elle parcourue à votre avis ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1Extrait du carnet de Lucile
« Je suis partie de Londres dont les coordonnées sont {\left(51^{\circ}~\mathrm{N}~; 0^{\circ}~\mathrm{E})\right.} pour aller jusqu'à Valencia en Espagne {\left(40^{\circ}~\mathrm{N}~; 0^{\circ}~\mathrm{E})\right.}. Puis je me suis dirigée vers Pékin {\left(40^{\circ}~\mathrm{N}~; 116^{\circ}~\mathrm{E})\right.}. J'ai ensuite fait {\text{4~450 km}} vers le Sud et {\text{12~900 km}} vers l'Ouest. C'est à partir de ce point que je suis revenue à Londres. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 2Terre
La Terre est assimilée à une sphère de rayon {\text{6~371 km}}. Le parallèle passant à {40^{\circ}~\mathrm{N}} a une longueur approximative de {\text{30~740 km}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 3Planisphère

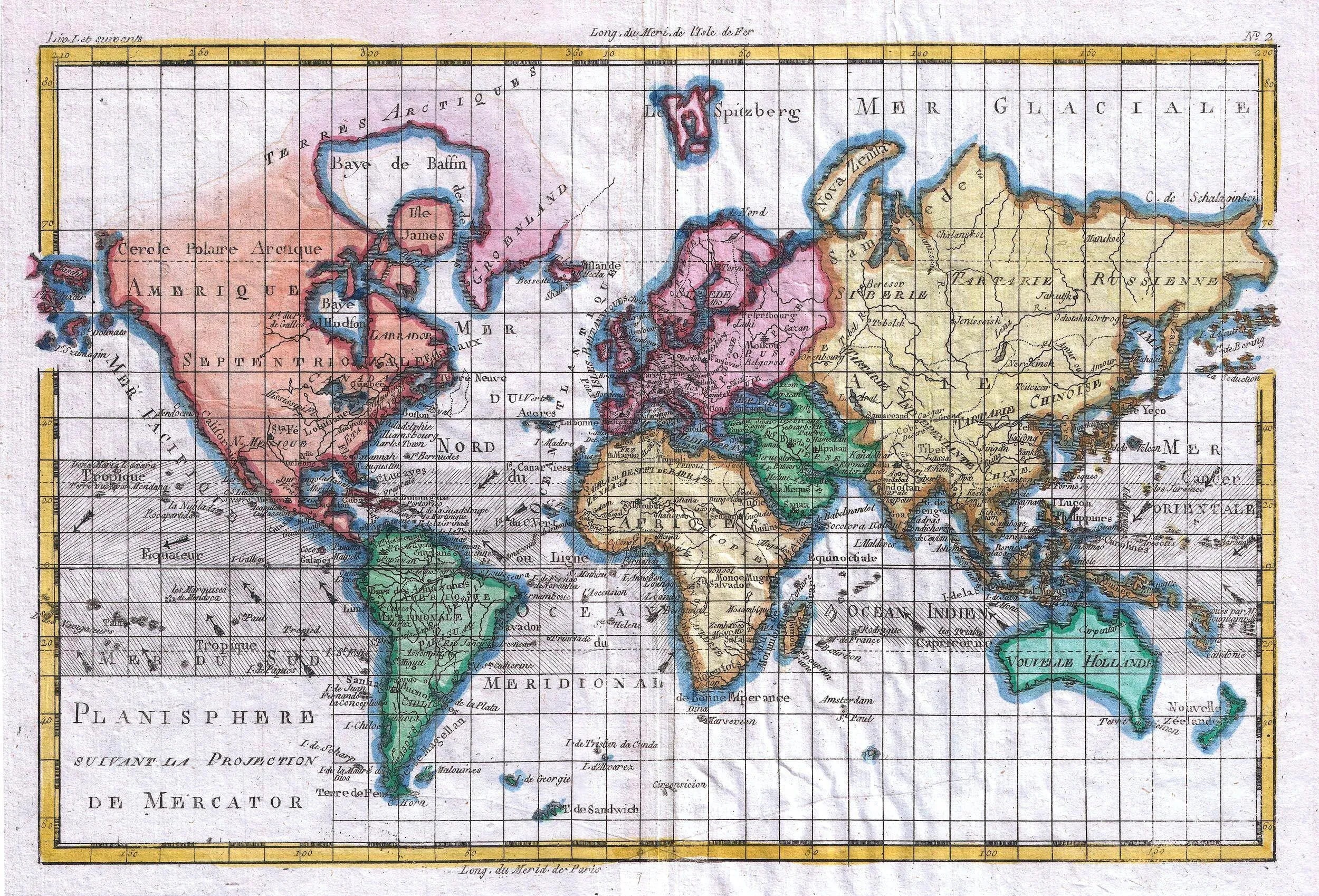
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

