Perspective cavalière
Un parallélépipède rectangle (ou pavé droit) est un solide possédant 6 faces, dont tous les angles sont des angles droits. Il a 8 sommets et 12 arêtes.

représentation d'un parallélépipède rectangle avec vu en pointillés des arêtes normalement non visibles

Dans la figure de gauche, on ne voit pas le point F ; il est sur la face arrière. La perspective cavalière permet de représenter ce que lʼon ne voit pas en réalité en traçant en pointillés les arêtes non visibles : [AF], [EF] et [FG].
En perspective cavalière :

les faces avant et arrière sont en vraie grandeur ;
les autres faces sont déformées par la perspective mais conservent le parallélisme.

Exercices n° 1 à 5
p. 334-335

Remarque : Un pavé droit dont toutes les faces sont des carrés est un cube.

Définition

Un patron est une figure plane qui permet de fabriquer le solide par pliage.
Le patron dʼun pavé droit est constitué de 6 faces rectangulaires. Les faces parallèles par pliage ont les mêmes dimensions.

Exercices n° 3, 6 et 7
p. 334

Patron d'un pavé droit

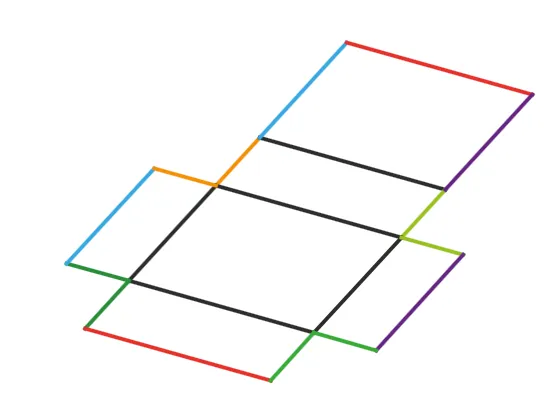
Remarque : Un pavé droit peut avoir plusieurs patrons possibles.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

2

J'approfondis
Se repérer dans un pavé droit

Repérage

Pour se repérer dans un pavé droit, il faut munir lʼespace dʼun repère composé dʼune origine et de 3 axes gradués perpendiculaires.
Les coordonnées dʼun point seront composées :

dʼune abscisse (x) ;
dʼune ordonnée (y) ;
dʼune altitude (z).

Dans la figure ci-dessous, O est lʼorigine du repère. Le point B, par exemple, a pour coordonnées (11 ; 0 ; 0) et F (11 ; 0 ; 6).

Pavé droit avec repère composé d'une origine et de 3 axes gradués perpendiculaires.

Exercices n° 8 à 10
p. 335

J'applique

Consigne : En utilisant la figure précédente, quelles sont les coordonnées des points E, C et G ?

Correction :

E (0 ; 0 ; 6) car E se situe sur lʼaxe z (altitude).
Pour aller de O à C, il faut 11 graduations en abscisse et 6 en ordonnées donc C (11 ; 6 ; 0).
Pour aller de O à G, il faut 11 graduations en abscisse, 6 en ordonnées et 6 en altitude donc G (11 ; 6 ; 6).

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

B
La sphère

Je découvre

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1
La sphère dans l'espace

Représentation

Perspective cavalière
La sphère de centre O et de rayon r est formée de tous les points M de lʼespace tels que OM = r.
La boule de centre O et de rayon r est formée de tous les points M de lʼespace tels que OM \leq r.

Exercices n° 11 à 12
p. 336

Aide

En résumé, la sphère est vide et la boule est pleine.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

2
Je perfectionne
Repérage sur une sphère

Repérage

Pour se repérer sur une sphère (par exemple la Terre), il faut des coordonnées géographiques : une latitude et une longitude exprimées en degrés.
Dans le cas de la Terre :

Horizontalement, la Terre est découpée selon des lignes parallèles qui sont utilisées pour déterminer la latitude. Le parallèle de référence est lʼéquateur (0°). Verticalement, la Terre est découpée en quartiers par des méridiens qui sont utilisés pour déterminer la longitude. Le méridien de référence est le méridien qui passe par la ville de Greenwich en Angleterre (0°).

Exercices n° 13 à 17
p. 336

Remarque :

La latitude est comprise entre 0° et 90° Nord ou Sud.
La longitude est comprise entre 0° et 180° Est ou Ouest.

J'applique

Consigne : Quelles sont les coordonnées du point M ?

Correction : M a pour coordonnées 40° Nord (latitude) et 70° Est (longitude).

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

C
Représentations de solides usuels et de sections planes

J'approfondis

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Les solides usuels

Solides	Perspective cavalière	Section
Pavé droit		La section dʼun pavé droit par un plan parallèle à une face est un rectangle de même dimension que la face.	La section dʼun pavé droit par un plan parallèle à une arête est un rectangle dont lʼune des dimensions est la longueur de cette arête.
Cylindre		La section dʼun cylindre par un plan parallèle à sa base est un cercle de même rayon que la base.	La section dʼun cylindre par un plan perpendiculaire à sa base est un rectangle dont une des dimensions est la hauteur du cylindre.
Cône de révolution		La section dʼun cône par un plan parallèle à sa base est une réduction de sa base, donc un cercle.
Pyramide		La section dʼune pyramide par un plan parallèle à sa base est une réduction de celle-ci, cʼest-à-dire de même forme que la base (les deux bases sont dites homothétiques).
Sphère		La section dʼune sphère par un plan est un cercle.