Chapitre 15
Problèmes résolus
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
✔ Je reconnais une situation de proportionnalité
✔ Je modèlise une situation à l'aide d'un schéma, d'un tableau ou d'un arbre
✔ Je modèlise une situation à l'aide d'un schéma, d'un tableau ou d'un arbre
Voici les coordonnées approximatives de deux villes :
Londres \text{(51° N ; 0° E)} et Yendi \text{(9° N ; 0°E)}. Londres et Yendi sont distantes de 4 683 km.
1. Quelle est la circonférence de la Terre ?
2. Quel est le rayon de la Terre ? Utilisez la notation scientifique pour exprimez votre résultat.
1. Quelle est la circonférence de la Terre ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1
Quand il nous est demandé de calculer une distance sur ou dans un volume, il peut être intéressant de se représenter ce volume. Dans le cas dʼune sphère qui représente la Terre, il faut avoir clairement à lʼesprit les « coupes » que représentent les méridiens et les parallèles. On représente ensuite les données du problème sur le schéma.

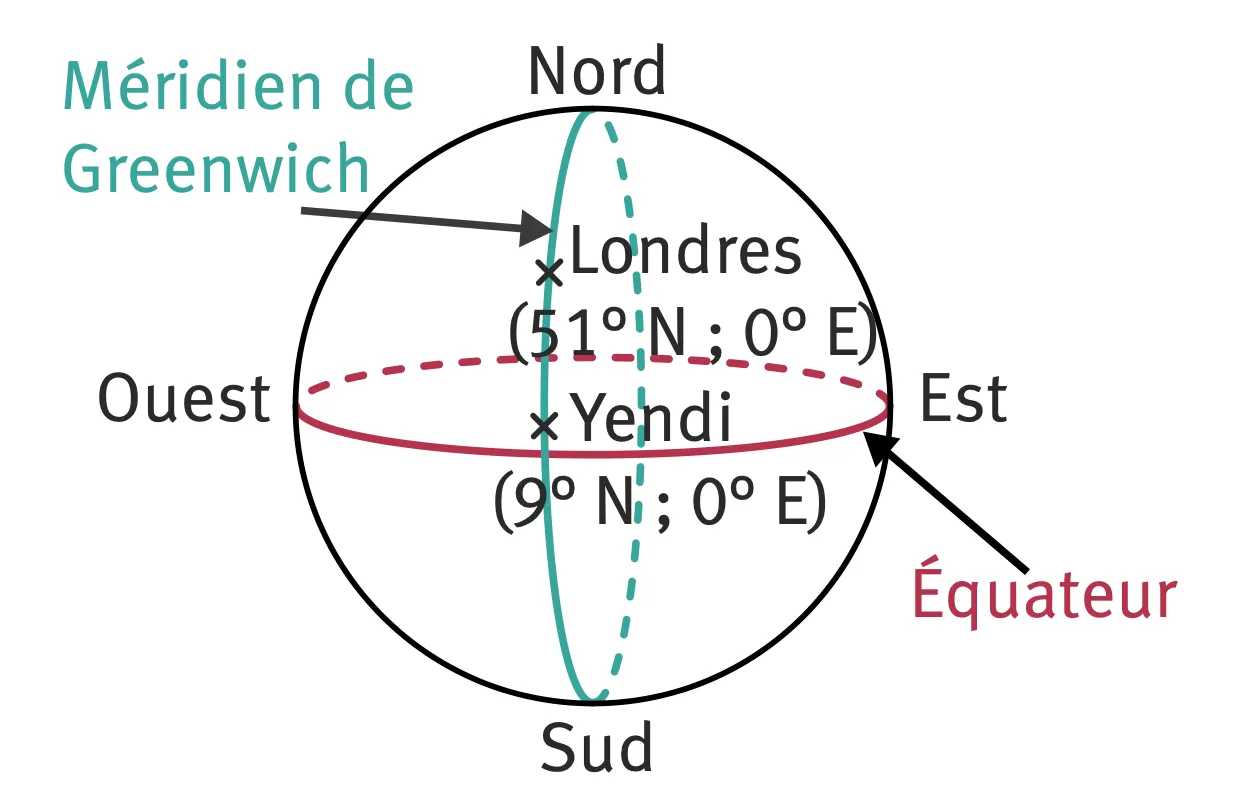
Corrigé 1


- Les points L et Y ont la même longitude et se trouvent donc sur un même grand cercle, dont le rayon correspond à celui de la Terre.
Lʼarc de cercle reliant les deux villes a une ouverture de 51^{\circ} - 9^{\circ} = 42^{\circ} et correspond à une distance de 4 683 km. La circonférence de la Terre correspond à un angle de 360^{\circ}. Cʼest une situation de proportionnalité.
Lʼégalité des produits en croix donne : 360 \times 4\:683 \div 42 = 40\:140.
La circonférence de la Terre est donc dʼenviron 40 140 km. - On obtient le rayon dʼun cercle en divisant son périmètre par 2 \pi .
40\:140 \div 2 \pi \approx 6\text{,}4 \times 10^3
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2
Quand il nous est demandé de trouver une valeur dʼune figure géométrique, on peut représenter cette figure à lʼaide dʼun logiciel de géométrie dynamique en gardant les proportions et les angles. Grâce au logiciel, on trouve alors la mesure voulue et on en déduit celles recherchées par proportionnalité.
Corrigé 2
Dans le logiciel :
Il sʼagit dʼune situation de proportionnalité. Pour un rayon de 1 cm, lʼarc de cercle mesure 0,733 cm. Pour un arc de cercle de 4 683 km, le rayon mesure donc environ :
4\:683 \times 1 \div 0\text{,}73 \approx \boldsymbol{6\textbf{,}4 \times 10^3} km.
Pour obtenir la circonférence, il suffit de multiplier le rayon par 2 \pi. La circonférence de la Terre est donc dʼenviron 40 140 km.
- Placer un point A.
- Placer les points B et B' tel que \text{AB = 1}, \text{AB}^{\prime} = 1 et \widehat{\text{BAB}^{\prime}} = 42^{\circ}.
Il sʼagit dʼune situation de proportionnalité. Pour un rayon de 1 cm, lʼarc de cercle mesure 0,733 cm. Pour un arc de cercle de 4 683 km, le rayon mesure donc environ :
4\:683 \times 1 \div 0\text{,}73 \approx \boldsymbol{6\textbf{,}4 \times 10^3} km.
Pour obtenir la circonférence, il suffit de multiplier le rayon par 2 \pi. La circonférence de la Terre est donc dʼenviron 40 140 km.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24Problème similaireÀ vol d'oiseau
La sphère suivante est assimilée à la Terre et que le rayon de la Terre est de 6 371 km.
Calculez la distance à vol dʼoiseau de NM.
Calculez la distance à vol dʼoiseau de NM.

Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

