Mathématiques Cycle 4
Mes Pages
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Ch. 7
Puissances
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et géométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Ch. 17
Agrandissements - réductions
Ch. 18
Trigonométrie
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Chapitre 13
Les maths autrement
Des aires surprenantes !
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Présentation
Vincenzo Viviani
Vincenzo Viviani (1622-1703) est un savant italien, disciple de Galilée. Il est à la fois mathématicien, physicien et astronome. Il est notamment connu pour avoir amélioré l'estimation de la vitesse du son en mesurant le délai entre l'étincelle et le bruit lors d'un tir de canon. Un théorème de géométrie sur les triangles équilatéraux porte également son nom.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Je mène à bien un calcul littéral.
- Je modélise une situation à l'aide d'une expression mathématique.
- Je représente des objets et des figures géométriques.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Étape 1Observation du théorème
1. Avec un logiciel de géométrie dynamique, construisez un triangle équilatéral ABC. Placez un point M à lʼintérieur de ce triangle.
2. Construisez d, e et f, trois droites passant par le point M et respectivement perpendiculaires aux côtés [AB], [BC] et [AC]. Nommez D, E et F les points dʼintersection respectifs de d et [AB], de e et [BC] et de f et [AC].
3. À lʼaide du logiciel, mesurez les longueurs MD, ME et MF.
4. Dans la ligne de saisie, créez un nombre n égal à la somme de ces trois longueurs.
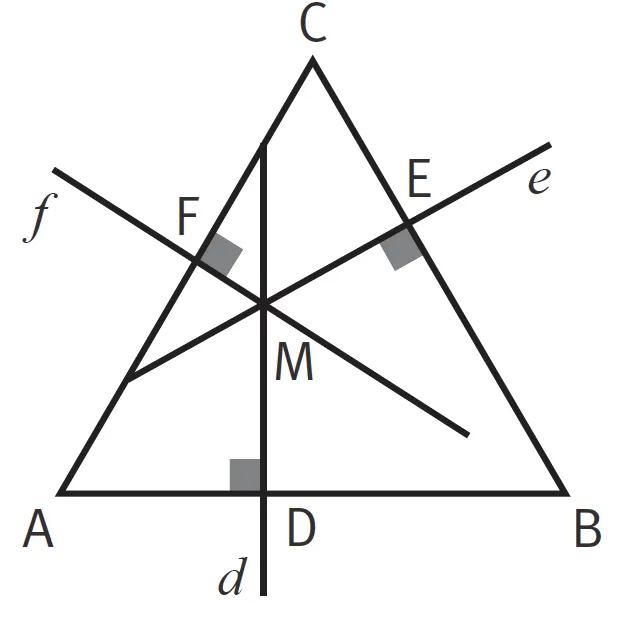
2. Construisez d, e et f, trois droites passant par le point M et respectivement perpendiculaires aux côtés [AB], [BC] et [AC]. Nommez D, E et F les points dʼintersection respectifs de d et [AB], de e et [BC] et de f et [AC].
3. À lʼaide du logiciel, mesurez les longueurs MD, ME et MF.
4. Dans la ligne de saisie, créez un nombre n égal à la somme de ces trois longueurs.
GeoGebra
5. Déplacez le point M. Que remarquez-vous quant à la valeur de cette somme ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Étape 2Une démonstration
On nomme h la longueur de la hauteur du triangle relative au côté [AB].
1. Écrivez une expression permettant de calculer lʼaire du triangle ABC en fonction des longueurs AB et h.
2. Écrivez trois expressions permettant de calculer les aires des triangles AMB, BMC et AMC à l'aide respectivement des mesures MD, MF et ME.
3. Écrivez une expression permettant de calculer lʼaire du triangle ABC à lʼaide des aires des triangles AMB, BMC et AMC.
4. Déduisez-en que \text{MD} + \text{ME} + \text{MF} = h.
Vous avez montré que la somme des distances aux trois côtés dʼun point intérieur à un triangle équilatéral est toujours égale à la hauteur du triangle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Envie d'en savoir plus ?
Découvrez à l'aide de triangles équilatéraux.
Découvrez à l'aide de triangles équilatéraux.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
