Nos classiques
Sommaire
Mes pages
N° Page
Thème 1 : Nombres et calculs
Thème 2 : Organisation et gestion de données
Thème 3 : Grandeurs et mesures
Thème 4 : Espace et géométrie
Annexes
Nos dossiers d'actualité
Dossier d'actualité
/ 443
Page précédente
Chapitre 5
Exercices

Questions Flash - Je m'entraine

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Questions flash

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
1. L'équation \bm{2x + 3 = 0} a pour solution :




2. La solution de l'équation \bm{(x + 3) \times 2 - 7 = x + 4} est :




3. Ces deux équations ont la même solution : \bm{8x - 4 = 0} et \bm{x + 1 = \dfrac{1}{2}}



4. Une inéquation ne peut avoir qu'une solution.



5. L'inéquation \bm{5x + 3 \leq 8 + x} est vraie pour...








6. Si \bm{(4 + x) - 1 = 3 + x} , cela signifie...





7. \bm{x} est un nombre tel que \bm{x > 5}. Quelles inégalités sont vérifiées ?






Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Je m'entraine

Résolution d'équations
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1
Testez des valeurs.

Soit l'équation (E) : 2x - 6 = 0.

1. Le nombre 0 est-il une solution de (E) ? Justifiez.
2.  Le nombre 3 est-il une solution de (E) ? Justifiez.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

2
Testez des valeurs.

✔ J'utilise des cas particuliers pour orienter ma démarche de résolution

Soit l'équation (E) : 2x^2 - 6x = 0.

1. Le nombre 0 est-il une solution de (E) ? Justifiez.
2.  Le nombre 3 est-il une solution de (E) ? Justifiez.
3.  Le nombre −3 est-il une solution de (E) ? Justifiez.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

3
Associez chaque solution à son équation.

6x + 2 = 50
7 = -3 -2x
22 = 4x - 6
22 = 4x + 6
22 = 6 - 4x
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

4
Associez chaque solution à son équation.

x + x + x = 10 - x
2x + 3 = 3x + 2
4(1 - x) = 18
5x × 2 = 4x + 24
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

5
Léonie, Nathalie, Samuel et Serge ont essayé de résoudre l'équation \bm{3(x - 4) = -4 - x}.

✔ J'exerce mon esprit critique pour vérifier la cohérence des résultats

Voici leurs copies corrigées par le professeur.

LéonieNathalie
\bcancel{\begin {array}{l} 3(x - 4) = -4 - x\\ 3x - 4 = -4 - x\\ 3x + x - 4 = - 4 - x + x\\ 4x - 4 = - 4\\ 4x = 0\\ x = 0\\ \end{array}}
FAUX !
3(x - 4) = -4 - x
3x - 12 = -4 - x
3x - 12 + x = -4 - x + x
4x - 12 = -4
4x - 12 + 12 = -4 + 12
4x = 8
x = 2
SamuelSerge
3(x - 4) = -4 - x
3x - 12 = -4 - x
3x - 12 + 4 = -4 - x + 4
3x - 8 = -x
3x - 8 + x = -x + x
4x - 8 = 0
4x - 8 + 8 = 0 + 8
4x = 8
x = 2
\bcancel{\begin {array}{l} 3(x - 4) = -4 - x \\ 3(x - 4) + 4 = -4 - x + 4 \\ 3x = -x \\ 3x + x = -x + x \\ 4x = 0 \\ x = 0 \end{array}}
FAUX !

1.  Vérifiez que x = 2 est une solution de lʼéquation et que x = 0 ne lʼest pas.
2.  Expliquez les erreurs que Léonie et Serge ont faites.
3.  Expliquez ce que Nathalie et Samuel ont fait à chaque transformation de lʼéquation.
4.  Expliquez pourquoi Nathalie a trouvé la solution plus rapidement que Samuel.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

6
Résolvez les équations suivantes.

1.  x + 4 = 12
2.  x + 5\text{,}1 = x + x
3.  6x = x - 15
4.  -14 = 2x
5.  5 = 4x
6.  x + 8 = 2x + 3
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

7
Résolvez les équations suivantes.

1.  3x + 7 = -13 - 2x
2.  3(2x - 3) = 27
3.  6(x - 3) = 3x
4.  2x - 9 = (5x + 7) \times (-3)
5.  0\text{,}5x - 2\text{,}6 = 3x + 1\text{,}4
6.  8x = (5x - 3) \times (-0\text{,}2)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

8
Résolvez les équations suivantes.

✔ Je mène à bien un calcul littéral

1.  3 = 2x + 8
2.  5x - 4 = -3x
3.  3\text{,}8 = 6x - 0\text{,}4
4.  6 + 2x = 0\text{,}5x
5.  x + x + x = 28 - 1
6.  10 = 5(x - 8)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

9
Par quelle valeur faut-il remplacer \bm{x} pour que les deux fractions soient égales ?

✔ J'utilise l'écriture d'un nombre la plus appropriée pour calculer

1.  \dfrac{x}{9} et \dfrac{1}{6}
2.  \dfrac{4}{x} et \dfrac{2}{3}
3.  \dfrac{13}{2} et \dfrac{x}{5}
4.  \dfrac{10}{3} et \dfrac{7}{x}
5.  \dfrac{x}{2} et \dfrac{3}{8}
6.  \dfrac{3}{x} et \dfrac{2}{5}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

10
Résolvez les équations suivantes.

1.  7x + 30 = 2x - 24
2.  2x + (8 + x) = 20
3.  6 - x = 7 + x
4.  2x + 6 = 4(x - 7)
5.  8 - (3 - 2x) = 3x
6.  \dfrac{1}{4} x = \dfrac{3}{2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

11
Résolvez les équations suivantes.

1.  34 - 4x = 5
2.  0\text{,}2x = -4\text{,}3
3.  3x + 2 = 8 - 2x
4.  3 - x = x + 9
5.  1\text{,}4 - 2x = -12 - 3x
6.  5x + 6 = 8 - x
7.  3\text{,}4x - 2x = -7
8.  3(3a - 3) = a
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

12
Résolvez les équations suivantes.

1.  6x - 4 = 3 \times (2 - x)
2.  2 \times \pi \times x = 10
3.  -\dfrac{1}{2} = \dfrac{1}{4}x + 5
4.  0\text{,}5x + 2 = 3x - 8
5.  2x = 3 \times \pi
6.  \dfrac{1}{3}x + \dfrac{2}{3}x = 5 + 2x
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

13
Résolvez les équations suivantes.

1.  9(x + 7) = 27(x +1)
2.  18(5x - 3) = 18(2x + 1)
3.  5(x + 4) = -3(x - 2)
 4.  6x - 3 = 3(x + 6)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

14
Kevin reçoit chaque mois 11,50 € d'argent de poche.

Il décide d'économiser tout son argent de poche jusqu'à avoir suffisamment dans sa tirelire pour pouvoir acheter le coffret de jeux vidéo de ses rêves qui coute 49,90 €.

1.  Combien de mois Kevin devra-t-il attendre avant de pouvoir acheter son coffret ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

15
Savoir refaire
Rectangles de longueur variable.

✔ Je modélise une situation à l'aide d'une expression mathématique

Deux rectangles : un de longueur x + 5 et de largueur 2 et un autre de longeur 10-2x et de largeur 3.
1.  Déterminez la valeur de x pour laquelle les deux rectangles ont la même aire.
2.  Déterminez la valeur de x pour laquelle les deux rectangles ont le même périmètre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

16
Aires.

Deux figures. Un trapèze de petite base égal à 3, de grande base égal à x et de hauteur 2. et un triangle de base égal à 3 et de hauteur égal à x.
1.  Déterminez la valeur de x pour laquelle le trapèze est de même aire que le triangle.
Coup de pouce
L'aire d'un trapèze est \frac{1}{2} \times(~petite \space base+ grande \space base) \times hauteur .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

17
Aude veut former la figure illustrée ci-dessous avec un fil métallique de 96 cm de longueur.

✔ Je mène à bien un calcul littéral
Croix pleine où la base vaut 2x, un côté et le retour vaut x
1.  Quelle est la valeur maximale que l'on peut choisir pour x ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

18
ABC est un triangle isocèle en C tel que AB = 14 cm.

1.  Quelle doit être la longueur des côtés [AC] et [BC] pour que le périmètre de ABC soit de 1 m ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

19
Voici deux rectangles ABCD et EFGH. Les dimensions sont données en cm.

✔ Je structure mon raisonnement

Les dimensions sont données en cm.
Deux retangles. ABCD où BC = x-4 et DC = 2x-3. Et EFGH où EH = x-4 et HG = x+2.
1.  Pour quelles valeurs de x ces deux rectangles peuvent-ils être construits ?
2.  Calculez les aires de ces rectangles lorsque x = 100. Sont-elles égales ? Que valent alors leurs périmètres ?
3.  Cherchez pour quelle(s) valeur(s) de x ces deux périmètres sont égaux.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

20
Déterminez la valeur de \bm{x} pour laquelle le cercle et le rectangle suivants ont le même périmètre.

Un cerle de rayon x et un rectangle de longueur égal à 3x et de largeur égal à 3
1.  Donnez une valeur approchée au centième de la solution.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

21
La somme entre le nombre qui me précède et moi-même est égale à 47.

1.  Quel nombre entier suis-je ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

22
Nous sommes trois nombres entiers consécutifs et notre somme est égale à 258.

✔ J'émets une hypothèse

1.  Qui sommes-nous ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

23
Si j'additionne un nombre, son double et son triple, j'obtiens 78.

1.  Quel est ce nombre ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Résolution d'inéquations
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

24
La somme d'un entier, de son double et de son triple est supérieure à 100.

Mais le plus grand de ces trois entiers est inférieur à 99.

1.  Déterminez les valeurs possibles du plus petit de ces trois entiers.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

25
De quel côté penche la balance dans chacun des cas suivants ?

Situation initiale :
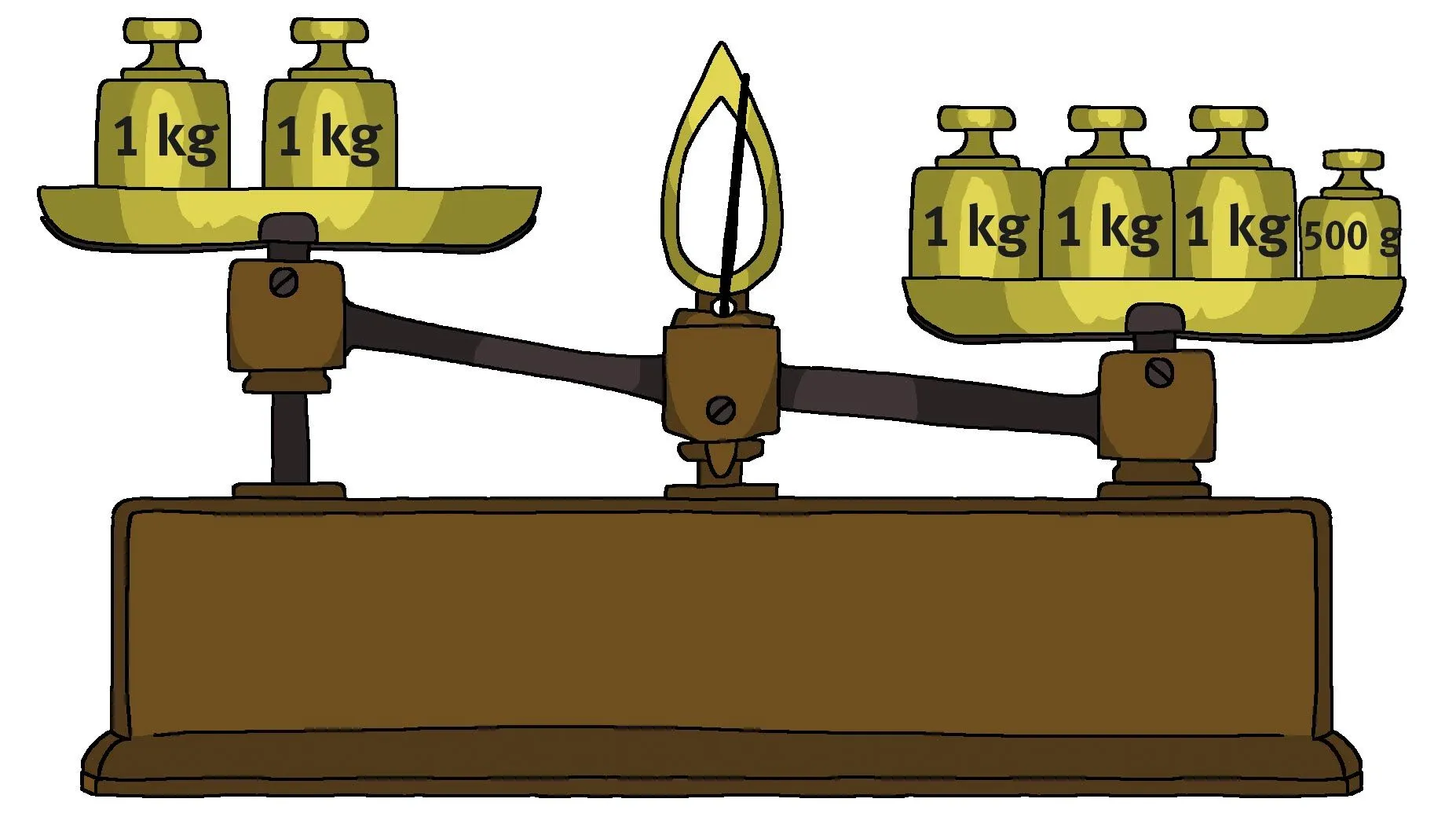
Placeholder pour Illustration d'une balance mécanique déséquilibrée : 2 kg à gauche, 3,5 kg à droite. La balance penche du côté droit.Illustration d'une balance mécanique déséquilibrée : 2 kg à gauche, 3,5 kg à droite. La balance penche du côté droit.
1.  On ajoute 300 g sur le côté gauche de la balance ?
2.  On ajoute 1,5 kg sur le côté gauche de la balance ?
3.  On ajoute 2 kg sur le côté gauche de la balance ?
4.  On enlève 300 g du côté droit ?
5.  On enlève 1,5 kg du côté droit ?
6.  On enlève 2 kg du côté droit ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

26
On considère l'inéquation suivante : \bm{(x + 3)(x - 2) \leq x^2 - 3x}.

1.  Justifiez que 0 est solution de cette inéquation.
2.  2 est-il solution de cette inéquation ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

27
Les nombres \bm{-3~; 6~; 1~; \dfrac{1}{ 3}~; 0,5} sont-ils solution des inéquations suivantes ?

✔ Je combine de façon approprié le calcul mental, posé et instrumenté

1.  3x + 6 > -2
2.  -5x - 1 \lt 1
3.  -0\text{,}5x + 6 \leq 11
 4.  x + 3 \geq 0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

28
Résolvez les inéquations suivantes.

1.  3x - 4 \leq 5
2.  -2x + 1 \leq 3
3.  5(x + 1) \leq 25
4.  9 \leq -3x \times -6
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

29
Résolvez les inéquations suivantes et représentez graphiquement l'ensemble des solutions.

✔ Je modélise une situation à l'aide d'un schéma, d'un tableau ou d'un arbre

1.  3x + 1 \leq 0
2.  4x \leq 16
3.  -5x \leq 5
4.  -x + 9 \leq 1
Logo Geogebra

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

30
Inégalités.

✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème

1.  Si x est un nombre tel que {x > 4}, que peut-on dire de {x + 4} ? Et de {x - 7} ?
2.  Si x est un nombre tel que {x \leq 8}, que peut-on dire de - x ? De 4x ?
3.  Si un nombre x est tel que {x \lt -3}, que peut-on dire de {4x + 2} ? Et de {-5x + 1} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

31
Résolvez les inéquations suivantes et représentez graphiquement l'ensemble des solutions.

1.  7x + 18 \leq -3
2.  -2x +5 \leq 15
3.  x - 7 \leq 7
4.  -10x \leq -3
Logo Geogebra

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

32
La somme de quatre entiers consécutifs est strictement supérieure à 100.

1.  Déterminez la plus petite valeur possible que peut prendre le plus petit des quatre nombres.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Parcours de compétences

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Énoncé

✔ Je modélise une situation à l'aide d'une expression mathématique

Mattéo aime aller au cinéma. Yasmine, en se documentant sur internet, trouve deux tarifs possibles :
Tarif 1 sans abonnement : 8,60 euros la place.
Tarif 2 avec abonnement : 6,25 euros la place et une carte dʼabonnement à 30 euros valable un an.

« À partir de combien de places ai-je intérêt à m'abonner ? » s'interroge-t-il. Qu'en pensez-vous ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Niveau 1

Je reconnais les éléments mathématiques dans l'énoncé.

Coup de pouce
Identifiez les nombres dans lʼénoncé. Expliquez à quoi correspond chacun dʼeux.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Niveau 2

Je classe les informations du problème entre celles qui sont connues et inconnues.

Coup de pouce
Listez ce que vous savez grâce à lʼénoncé. Quelle information manque-t-il pour connaitre le prix total payé par Mattéo chaque année dans chacun des cas ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Niveau 3

J'identifie les opérations nécessaires à la résolution du problème.

Coup de pouce
Expliquez quelle démarche mathématique permet de comparer deux expressions.
Dans cet exercice, que cherche-t-on à comparer ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Niveau 4

J'exprime les informations du problème en fonction des inconnues.

Coup de pouce
Répondre à la question correspond à résoudre une inéquation.
Page suivante

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.