Sommaire
Mes pages
N° Page
ouverture
p. 1-12
Thème 1 : Nombres et calculs
Thème 2 : Organisation et gestion de données
Thème 3 : Grandeurs et mesures
Thème 4 : Espace et géométrie
Annexes
Nos dossiers d'actualité
Dossier d'actualité
/ 443
Page précédente
Chapitre 5
J'apprends

Équations et inéquations

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

A
Résolution d'équations

J'approfondis
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1
Notions d'équation, de solution

Définitions
On met deux expressions littérales en équation quand on veut savoir pour quelles valeurs des variables les membres de droite et de gauche sont égaux.

\underbrace{\color{#5438E0}{3 \times x+2}}=\underbrace{\color{#006141}{x + 6}} \\ {\color{#5438E0}\text{membre de gauche}} \space\space\space {\color{#006141}\text{membre de droite}}

Dans une équation, les lettres utilisées sont appelées des inconnues parce quʼon ne connait pas leur valeur quand on écrit lʼéquation.
On dit quʼun nombre est solution dʼune équation quand lʼégalité est vraie lorsquʼon remplace une inconnue par ce nombre.

Exercices n° 
1 à 23
 p. 108 - 110.

Exemple :
  • Le nombre x = 2 est une solution de lʼéquation précédente car quand on remplace x par 2, les deux membres prennent la même valeur :
    3 \times 2 + 2 = 6 + 2 = 8 et 2 + 6 = 8.
  • Le nombre x = 5 nʼest pas une solution de lʼéquation précédente car quand on remplace x par 5, les deux membres nʼont pas la même valeur :
    3 \times 5 + 2 = 15 + 2 = 17 et 5 + 6 = 11.
 
Définition
Résoudre une équation, cʼest trouver toutes ses solutions.

Exercices n° 
1 à 23
 p. 108 - 110.

Exemple :
Lʼéquation 2x = 5 a une seule solution : \dfrac{5}{2}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

2
Résolution d'une équation à une inconnue, du premier degré

Propriétés
  • Une égalité est toujours valable lorsquʼon additionne ou soustrait un même nombre aux deux membres de lʼégalité.
  • Une égalité est toujours valable lorsquʼon multiplie ou divise les deux membres de lʼégalité par un même nombre non nul.
Ainsi, si a = b : 
  • a {\color{#99331F}~+ \space c} = b {\color{#99331F}~+ \space c}
  • a {\color{#99331F}~\times \space c} = b {\color{#99331F}~\times \space c}
  • a {\color{#99331F}~- \space c} = b {\color{#99331F}~- \space c}
  • Si c \neq 0, \dfrac{a}{{\color{#99331F}c}} = \dfrac{b}{{\color{#99331F}c}}
Exercices n° 
1 à 23
 p. 108 - 110.
Méthode
Pour résoudre une équation :
  • On applique des opérations successives aux deux membres de lʼéquation dans le but dʼavoir lʼinconnue dʼun seul côté. On obtient ainsi la valeur de lʼinconnue.
  • On vérifie que chaque valeur trouvée est bien solution de lʼéquation.

Exercices n° 
1 à 23
 p. 108 - 110.

  

J'applique

Consigne :
Résolvez 10x - 99 = x + 18.

Correction :
  • Supposons 10x - 99 = x + 18
    donc 10x - x - 99 = x -  x + 18 (on retranche x)
    donc 9x - 99 = 18
    donc 9x - 99 + 99 = 18 + 99 (on ajoute 99)
    donc 9x = 117
    donc 9x \div 9 = 117 \div 9 (on divise par 9)
    donc x = 13
  • On vérifie pour x = 13
    10x - 99 = 10 \times 13 - 99 x + 18 = 13 + 18
         = 31       = 31
  • Donc 13 est la seule solution de cette équation.
Attention
Il ne faut surtout pas oublier lʼétape de vérification !
 

Propriété
Un produit est nul si et seulement si lʼun de ses facteurs est nul.
Donc souvent pour résoudre des équations :
  • On met tous les termes du même côté du signe « = » ;
  • On factorise ;
  • On trouve les valeurs de lʼinconnue pour lesquelles au moins un des facteurs est nul.

Exercices n° 
1 à 23
 p. 108 - 110.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

B
Résolution d'inéquations

Je perfectionne
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1
Inégalités strictes et larges

Définition
Pour comparer des nombres, on utilise deux types de symboles :
  • Les symboles larges :
    • a \geq b : a est supérieur ou égal à b ;
    • a \leq b : a est inférieur ou égal à b.
  • Les symboles stricts :
    • a > b : a est strictement supérieur à b ;
    • a \lt b : a est strictement inférieur à b.

Exercices n° 
24 à 32
 p. 110 - 111.

Exemple :
Lʼinégalité 1 \leq x \lt 3 est vérifiée pour tous les nombres allant de 1 (inclus) à 3 (exclu) et peut être représentée sur une droite graduée.
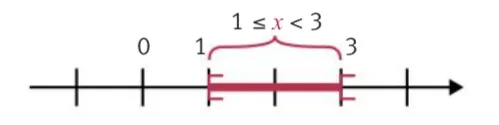Placeholder pour Graphique : droite numérique montrant l'intervalle 1 ≤ x < 3.Graphique : droite numérique montrant l'intervalle 1 ≤ x < 3.
Le sens des crochets a une signification :
  • Lorsque le crochet est ouvert vers lʼextérieur de la ligne, la valeur nʼest pas une solution. Ici, 3 nʼest pas une valeur possible de x.
  • Lorsque le crochet est ouvert vers lʼintérieur de la ligne, la valeur est solution. Ici, 1 est une valeur possible de x.
Remarque : Le contraire de a \lt b est a \geq b. Le contraire de a>b est a \leq b. a \leq b et b \geq a sont équivalentes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

2
Notions d'inéquation

Définitions
On met deux expressions littérales en inéquation quand on veut savoir pour quelles valeurs des inconnues les membres de droite et de gauche vérifient une inégalité.

\underbrace{\color{#5438E0}{3 \times x+2}} > \underbrace{\color{#006141}{x + 6}} \\ {\color{#5438E0}\text{membre de gauche}} \space\space\space {\color{#006141}\text{membre de droite}}

On dit quʼun nombre est solution dʼune inéquation quand lʼinégalité est vérifiée lorsquʼon remplace une inconnue par ce nombre.
Résoudre une inéquation, cʼest trouver toutes ses solutions.

Exercices n° 
24 à 32
 p. 110 - 111.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

3
Résolution d'une inéquation à une inconnue, du premier degré

Propriété
  • On obtient une inégalité de même sens lorsquʼon additionne ou soustrait un même nombre à chacun des membres de lʼinégalité.
  • On obtient une inégalité de même sens lorsquʼon multiplie ou divise par un même nombre strictement positif chacun des membres de lʼinégalité.
  • On obtient une inégalité de sens contraire lorsquʼon multiplie ou divise par un même nombre strictement négatif chacun des membres de lʼinégalité.

Exercices n° 
24 à 32
 p. 110 - 111.
Méthode
Pour résoudre une inéquation, on applique des opérations successives aux deux membres de lʼinéquation jusquʼà ce que lʼon ait uniquement lʼinconnue dʼun côté. On obtient ainsi la valeur de lʼinconnue.
Exercices n° 
24 à 32
 p. 110 - 111.

J'applique

Consigne :
Résolvez 10x - 33 \lt x + 3.

Correction :
  • Supposons 10x - 33 \lt x + 3
    donc 10x - x - 33 \lt x - x + 3 (on retranche x)
    donc 9x - 33 \lt 3
    donc 9x - 33 + 33 \lt 3 + 33 (on ajoute 33)
    donc 9x \lt 36

    donc 9x \times \dfrac{1}{9} \lt 36 \times \dfrac{1}{9} (on multiplie par \dfrac{1}{9} > 0)

    donc x \lt \dfrac {36}{9}

    donc x \lt 4
  • Les solutions de cette inéquation sont les nombres x tels que x \lt 4.
  • On représente les résultats sur une droite graduée.
    Placeholder pour Illustration : droite numérique graduée de 0 à 4.Illustration : droite numérique graduée de 0 à 4.

J'applique

Consigne :
Résolvez l'inéquation suivante : -2x + 6 \leq 12.

Correction :
  • Supposons - 2x + 6 \leq 12 
    donc -2x + 6 - 6 \leq 12 - 6 (on soustrait 6)
    donc -2x \leq 6
    donc \left(-2x\right) \times \left(- \dfrac{1}{2}\right) \geq 6 \times \left(-\dfrac {1}{2}\right) (on multiplie par \left(-\dfrac{1}{2}\right) ou on divise par \left(-2\right) qui sont strictement négatifs, donc le sens de l'inégalité change.)
    donc x \geq -3
  • Les solutions de -2x + 6 \leq 12 sont les nombres x \geq -3.
  • On les représente sur la droite graduée ci-dessous.
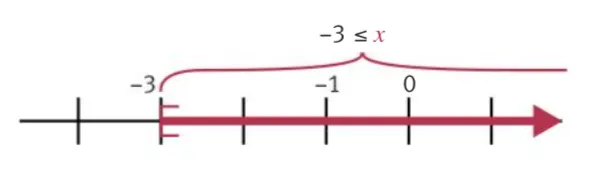
    Placeholder pour Graphique: droite numérique représentant l'inéquation -3 ≤ x. Les valeurs supérieures ou égales à -3 sont colorées en rouge.Graphique: droite numérique représentant l'inéquation -3 ≤ x. Les valeurs supérieures ou égales à -3 sont colorées en rouge.
Attention
On change le sens de lʼinéquation si on la multiplie ou divise par un nombre strictement négatif.

Remarque : Pour éviter de multiplier lʼinéquation par un nombre négatif, on aurait pu écrire :
-2x + 6 \leq 12
donc -2x + 6 - 12 \leq 12 - 12 (on soustrait 12)
donc -2x - 6 \leq 0
donc -2x - 6 + 2x \leq 0 + 2x (on ajoute 2x)
donc -6\leq 2x
donc \dfrac{-6}{2} \leq \dfrac{2}{2}x (on divise par 2, et 2 > 0).
donc -3 \leq x

Attention
À chaque fois que lʼon multiplie une inégalité par un nombre, il faut penser à préciser si ce nombre est positif (ou négatif) pour justifier que lʼinégalité ne change pas de sens (ou, au contraire, change de sens).

Remarque : Une équation ou une inéquation peut aussi être résolue à lʼaide dʼun graphique.
On représente dʼabord les deux membres de lʼéquation ou de lʼinéquation dans un même repère orthogonal. Ensuite on utilise ces représentations pour voir pour quelles valeurs de x chaque membre est supérieur, égal ou inférieur à lʼautre.

Exemple :
Pour résoudre lʼinéquation x + 1 \leq 5 - x, on trace le graphique :  
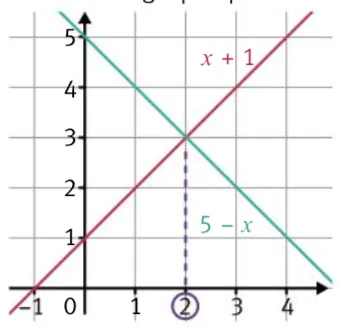
Placeholder pour Graphique : résolution graphique système équations linéaires (y = x + 1 et y = 5 - x). Intersection des droites au point (2, 3).Graphique : résolution graphique système équations linéaires (y = x + 1 et y = 5 - x). Intersection des droites au point (2, 3).
On a donc x + 1 \leq 5 - x pour tous les x où la courbe représentatrice de x + 1 est en dessous de celle représentatrice de 5 - x soit x \leq 2.
Notez que lʼon voit ici que x + 1 = 5 - x pour x = 2.
Page suivante

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille