ABC est un triangle rectangle et isocèle en B. On construit le symétrique de ABC par rapport à la droite (AC). Le symétrique du point B est appelé B'. Puis on place le point D à lʼintersection du segment [AC] et du segment [BB'].

Aide

carré ABCB' où ses diagonales se coupent en D. On sait que AD = DC = BD = DB' et AB' = B'C = CB = BA

Le zoom est accessible dans la version Premium.

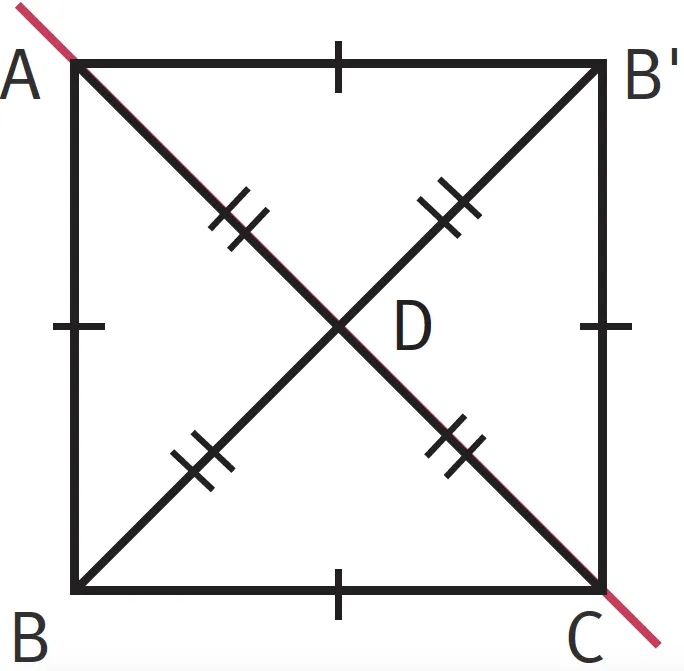Tracer la figure est très utile pour se représenter le problème et trouver la solution.Pensez à bien coder la figure pour synthétiser toutes les données.

Montrez que (AD) est une médiatrice du triangle ABB'.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Méthode 1

Pour démontrer des propriétés de figures de géométrie plane, il peut être efficace dʼutiliser des propriétés de la symétrie axiale.

Corrigé 1

B' est le symétrique de B par rapport à (AC), donc (AC) est la médiatrice de [BB'].
D appartient à (AC) donc (AD) et (AC) sont confondues. Donc (AD) est aussi la médiatrice de [BB']. (AD) est donc une médiatrice de ABB'.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Méthode 2

Il est également possible de repérer les figures particulières et dʼutiliser leurs propriétés pour résoudre le problème.

Corrigé 2

ABC est un triangle isocèle et rectangle en B, donc AB = BC. La symétrie axiale conserve les longueurs, donc AB = BC = AB' = B'C, donc ABCB' est un losange.
On sait que lʼangle \widehat{\text{ABC}} est droit, puisque ABC est rectangle en B.
ABCB' est donc un losange avec un angle droit, cʼest donc un carré.
Or les diagonales dʼun carré se coupent perpendiculairement et en leur milieu. Donc D est le milieu de [BB'] et [BB'] est perpendiculaire à [AD].

On en déduit donc que (AD) coupe [BB'] en son milieu et perpendiculairement, cʼest donc la médiatrice de [BB'].
Donc (AD) une médiatrice de ABB'.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

31
Problème similaire
Triangle équilatéral et symétrique.

ABC est un triangle équilatéral. D est le symétrique de A par rapport à (BC). E est le point dʼintersection de (AD) et (BC).

Montrez que [BE] est une hauteur et une médiatrice du triangle ABD.

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

Oups, une coquille

j'ai une idée !

Nous préparons votre pageNous vous offrons 5 essais

Yolène

Émilie

Jean-Paul

Fatima

Sarah

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Problèmes résolus

30Symétriques et médiatrices.

31Problème similaireTriangle équilatéral et symétrique.

Une erreur sur la page ? Une idée à proposer ?

Nous préparons votre pageNous vous offrons 5 essais

30
Symétriques et médiatrices.

31
Problème similaire
Triangle équilatéral et symétrique.