Chapitre 13
Exercices
Questions Flash - Je m'entraine
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions flash
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. On considère un triangle ABC tel que AB = 6,1 cm et BC = 2,7 cm. Quelles sont les valeurs de AC pour lesquelles il est possible de construire le triangle non plat ABC ?
2. Un triangle rectangle possède...
3. ABC est un triangle rectangle en A tel que {\widehat{\text{ABC}} = 35^{\circ}}. Alors :
4. On prend un triangle ABC tel que AB = 6,7 cm ; ABC = 60^{\circ} et BC = 6,7 cm. Alors on sait que...
2. Un triangle rectangle possède...
3. ABC est un triangle rectangle en A tel que {\widehat{\text{ABC}} = 35^{\circ}}. Alors :
4. On prend un triangle ABC tel que AB = 6,7 cm ; ABC = 60^{\circ} et BC = 6,7 cm. Alors on sait que...
5. MNO est un triangle isocèle en M tel que {\widehat{\text{NMO}} = 40^{\circ}}, alors :
6. MNO est un triangle isocèle en M. La droite d, passant par M, est perpendiculaire à (NO) et coupe [NO] en son milieu. On peut dire que...
7. PQR est un triangle quelconque. d est une droite passant par R et perpendiculaire à (PQ).
8. Le triangle OPC est isocèle en O, on a donc...
9. Deux triangles semblables sont toujours égaux.
6. MNO est un triangle isocèle en M. La droite d, passant par M, est perpendiculaire à (NO) et coupe [NO] en son milieu. On peut dire que...
7. PQR est un triangle quelconque. d est une droite passant par R et perpendiculaire à (PQ).
8. Le triangle OPC est isocèle en O, on a donc...
9. Deux triangles semblables sont toujours égaux.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je m'entraine
Les propriétés des triangles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Triangle
1. Un triangle OUA peut-il être isocèle en U et rectangle en O ? Si cʼest le cas, tracez un tel triangle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Construisez les triangles suivants.
1. \mathrm{ABC} tel que \widehat{\mathrm{ABC}}=120^{\circ} ; \mathrm{AB}=6 \mathrm{~cm} et \mathrm{BC}=12 \mathrm{~cm}.
2. \text {FGH} tel que \text {FGH}=45^{\circ} ; \mathrm{GH}=10 \mathrm{~cm} et \mathrm{GHF}=32^{\circ}.
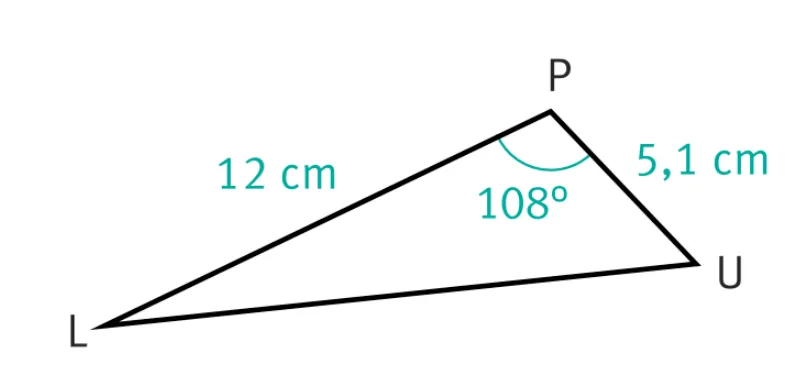
3. Le triangle LPU présenté ci-suit.

4. \text{MOS} tel que \text{MO} = 11 \mathrm{~cm} ; \text{OS} = 13,4\mathrm{~cm} et \text{SM} = 7,7 \mathrm{~cm}.
2. \text {FGH} tel que \text {FGH}=45^{\circ} ; \mathrm{GH}=10 \mathrm{~cm} et \mathrm{GHF}=32^{\circ}.
3. Le triangle LPU présenté ci-suit.


4. \text{MOS} tel que \text{MO} = 11 \mathrm{~cm} ; \text{OS} = 13,4\mathrm{~cm} et \text{SM} = 7,7 \mathrm{~cm}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3 Construisez les triangles suivants.
✔ Je réalise des figures, des schémas, des représentations d'objets
1. DEF tel que DE = 7 cm ; EF = 6 cm et DF = 4,9 cm.
2. SRT tel que SR = 8,5 cm ; \widehat{\text{SRT}} = 56^{\circ} et \widehat{\text{TSR}} = 65^{\circ}.
3. Le triangle ABD présenté ci-contre.

4. Le triangle ABO présenté ci-contre.

5. USC tel que SC = 4,2 cm ; CU = 5,4 cm et \widehat{\text{SCU}}= 38^{\circ}.
1. DEF tel que DE = 7 cm ; EF = 6 cm et DF = 4,9 cm.
2. SRT tel que SR = 8,5 cm ; \widehat{\text{SRT}} = 56^{\circ} et \widehat{\text{TSR}} = 65^{\circ}.
3. Le triangle ABD présenté ci-contre.

4. Le triangle ABO présenté ci-contre.

5. USC tel que SC = 4,2 cm ; CU = 5,4 cm et \widehat{\text{SCU}}= 38^{\circ}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4 Construisez les triangles suivants lorsque cʼest possible.
✔ J'exerce mon esprit critique pour vérifier la cohérence des résultats
1. ARG tel que AR = 4 cm ; RG = 8 cm et AG = 3 cm.
2. FDK tel que FD = 13,2 cm ; DK = 97 mm et FK = 5,5 cm.
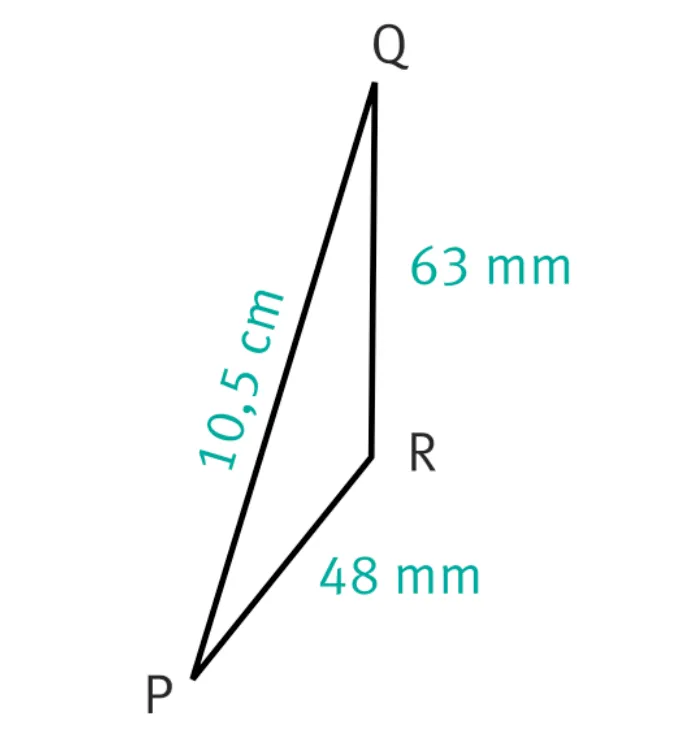
3. Le triangle PQR présenté ci-contre.

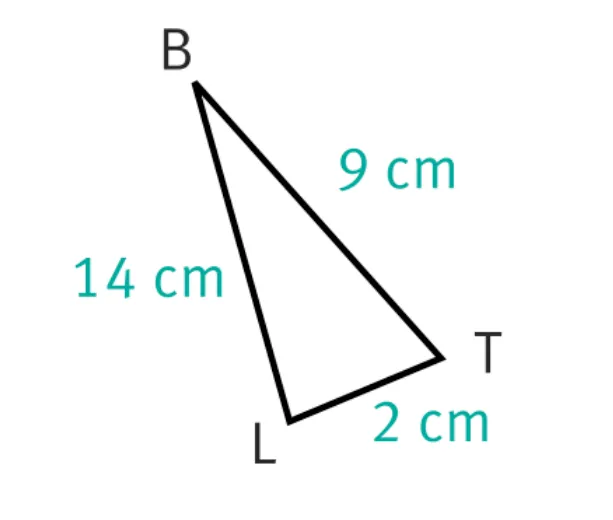
4. Le triangle BLT présenté ci-contre.

1. ARG tel que AR = 4 cm ; RG = 8 cm et AG = 3 cm.
2. FDK tel que FD = 13,2 cm ; DK = 97 mm et FK = 5,5 cm.
3. Le triangle PQR présenté ci-contre.


4. Le triangle BLT présenté ci-contre.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5 Construisez les triangles suivants lorsque cʼest possible.
✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème
1. ALO tel que AL = 7,8 cm ; \widehat{\text{ALO}} = 82^{\circ} et AO = 9 cm.
2. URT tel que UR = RT = 7 cm et \widehat{\text{RTU}} = 65^{\circ}.
3. HNR tel que HN = HR = 4,7 cm et NR = 9,5 cm.
4. GTY rectangle en Y tel que \widehat{\text{TYG}} = 34^{\circ}.
5. LPO tel que LP = 10 cm ; \widehat{\text{LPO}} = 20^{\circ} et \widehat{\text{POL}} = 104^{\circ}.
6. JHG tel que HG = 6,3 cm ; \widehat{\text{JHG}} = 78^{\circ} et \widehat{\text{HGJ}} = 104^{\circ}.
1. ALO tel que AL = 7,8 cm ; \widehat{\text{ALO}} = 82^{\circ} et AO = 9 cm.
2. URT tel que UR = RT = 7 cm et \widehat{\text{RTU}} = 65^{\circ}.
3. HNR tel que HN = HR = 4,7 cm et NR = 9,5 cm.
4. GTY rectangle en Y tel que \widehat{\text{TYG}} = 34^{\circ}.
5. LPO tel que LP = 10 cm ; \widehat{\text{LPO}} = 20^{\circ} et \widehat{\text{POL}} = 104^{\circ}.
6. JHG tel que HG = 6,3 cm ; \widehat{\text{JHG}} = 78^{\circ} et \widehat{\text{HGJ}} = 104^{\circ}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6 Construisez les triangles suivants lorsque cʼest possible.
1. OMG tel que MO = 5 cm ; OG = 12 cm et \widehat{\text{OMG}} = \widehat{\text{MGO}} = 76^{\circ}.
2. LSV tel que LS = 2 cm ; SV = 19 cm et \widehat{\text{LSV}} = 162^{\circ}.
3. AFR tel que AF = FR = 15 cm et \widehat{\text{AFR}} = 55^{\circ}.
4. ABE rectangle en E tel que AE = 62,5 cm et \widehat{\text{ABE}} = \widehat{\text{EAB}} = 34^{\circ}.
2. LSV tel que LS = 2 cm ; SV = 19 cm et \widehat{\text{LSV}} = 162^{\circ}.
3. AFR tel que AF = FR = 15 cm et \widehat{\text{AFR}} = 55^{\circ}.
4. ABE rectangle en E tel que AE = 62,5 cm et \widehat{\text{ABE}} = \widehat{\text{EAB}} = 34^{\circ}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7 Calculez la mesure du troisième angle dans les triangles suivants.
1. CDI tel que \widehat{\text{CDI}} = 12^{\circ} et \widehat{\text{DIC}} = 100^{\circ}.
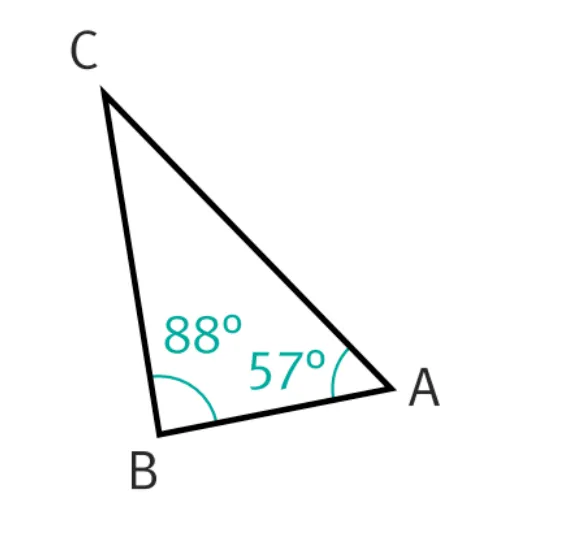
2. Dans le triangle ABC.

3. Dans le triangle GHT.

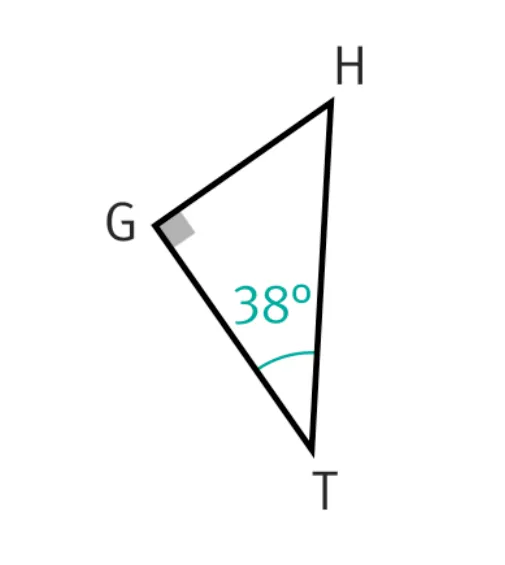
4. FRH tel que \widehat{\text{RHF}} = 77^{\circ} et \widehat{\text{FRH}} = 41^{\circ}.
2. Dans le triangle ABC.


3. Dans le triangle GHT.


4. FRH tel que \widehat{\text{RHF}} = 77^{\circ} et \widehat{\text{FRH}} = 41^{\circ}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8 Donnez la mesure des angles manquants dans les triangles suivants.
1. Dans le triangle ARN.

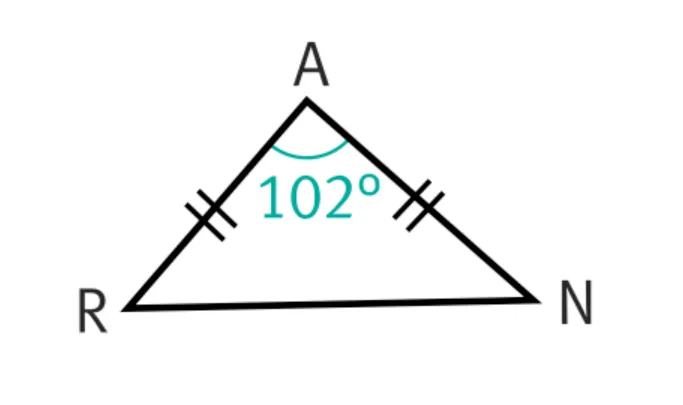
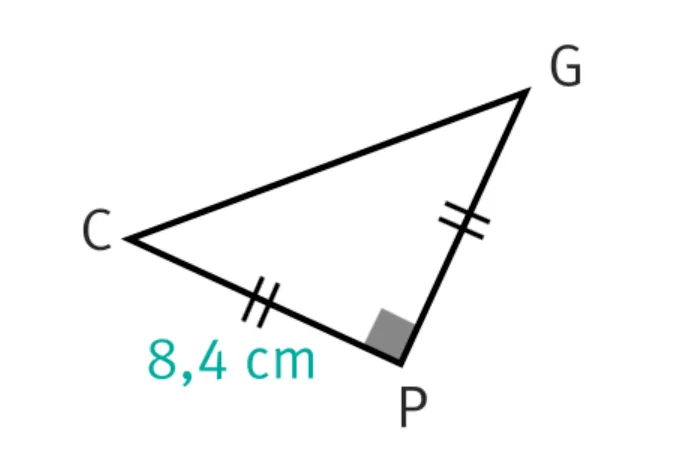
2. Dans le triangle CGP.

3. RIO tel que \widehat{\text{IRO}} = 94^{\circ} et RI = RO = 13,7 cm.
4. CPS rectangle en P tel que \widehat{\text{PSC}} = 12^{\circ}.


2. Dans le triangle CGP.


3. RIO tel que \widehat{\text{IRO}} = 94^{\circ} et RI = RO = 13,7 cm.
4. CPS rectangle en P tel que \widehat{\text{PSC}} = 12^{\circ}.
5. Dans le triangle ENI.

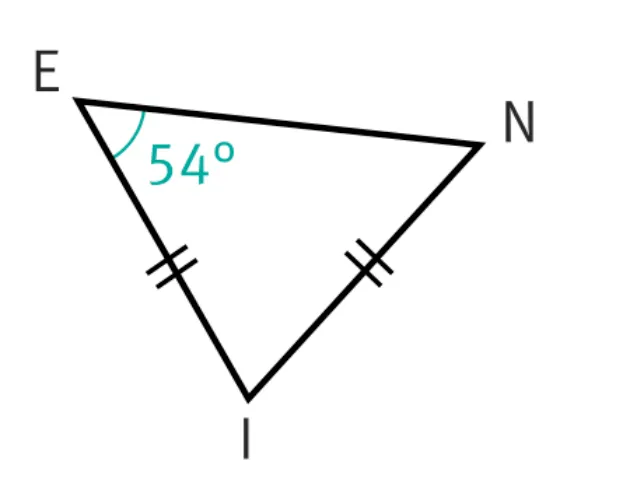
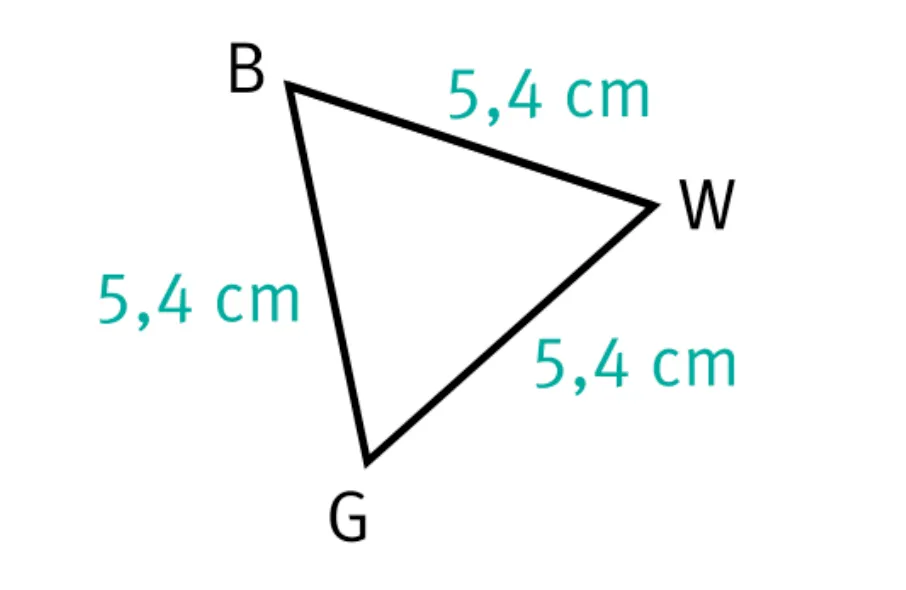
6. Dans le triangle BWG.

7. TPL isocèle en T telque \widehat{\text{LTP}} = 68^{\circ}.
8. JKL tel que JK = KL et JK = JL = 8,1 cm.


6. Dans le triangle BWG.


7. TPL isocèle en T telque \widehat{\text{LTP}} = 68^{\circ}.
8. JKL tel que JK = KL et JK = JL = 8,1 cm.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9 Vrai ou faux ?
1. Un triangle isocèle est équilatéral.
2. Un triangle équilatéral est isocèle.
3. Dans un triangle rectangle, les angles adjacents à lʼhypoténuse sont de même mesure.
4. Un triangle peut être équilatéral et rectangle.
2. Un triangle équilatéral est isocèle.
3. Dans un triangle rectangle, les angles adjacents à lʼhypoténuse sont de même mesure.
4. Un triangle peut être équilatéral et rectangle.
5. Un triangle qui a deux angles de même mesure est isocèle.
6. Un triangle peut avoir deux angles droits.
7. Un triangle qui possède deux angles de 60^{\circ} a ses trois côtés de même longueur.
6. Un triangle peut avoir deux angles droits.
7. Un triangle qui possède deux angles de 60^{\circ} a ses trois côtés de même longueur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10 Les triangles suivants sont-ils particuliers ? Si cʼest le cas, précisez leur nature.
✔ J'extrais et j'exploite les informations utiles d'un document
1. HLC tel que \widehat{\text{HLC}} = 80^{\circ} et \widehat{\text{LCH}} = 40^{\circ}
2. UNB tel que \widehat{\text{NBU}} = 75^{\circ} et \widehat{\text{BUN}} = 40^{\circ}.
2. UNB tel que \widehat{\text{NBU}} = 75^{\circ} et \widehat{\text{BUN}} = 40^{\circ}.
3. RTS tel que \widehat{\text{RTS}} = 108^{\circ} et \widehat{\text{TSR}} = 36^{\circ}.
4. GJF tel que \widehat{\text{GJF}} = 8^{\circ} et \widehat{\text{JFG}} = 82^{\circ}.
4. GJF tel que \widehat{\text{GJF}} = 8^{\circ} et \widehat{\text{JFG}} = 82^{\circ}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11 Nature de triangles.
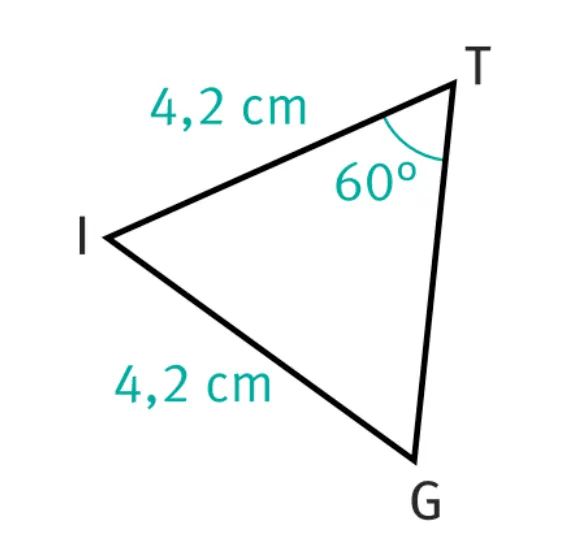
1. Le triangle ITG est-il particulier ? Si oui précisez sa nature.

2. Le triangle SPG est-il particulier ? Si oui précisez sa nature.

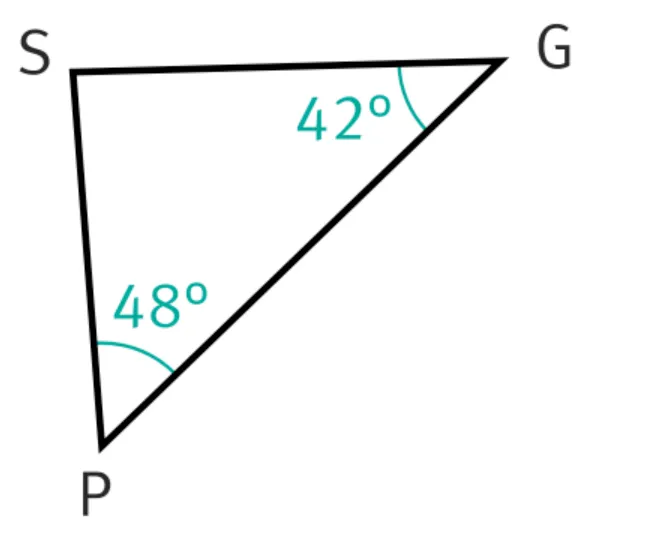


2. Le triangle SPG est-il particulier ? Si oui précisez sa nature.


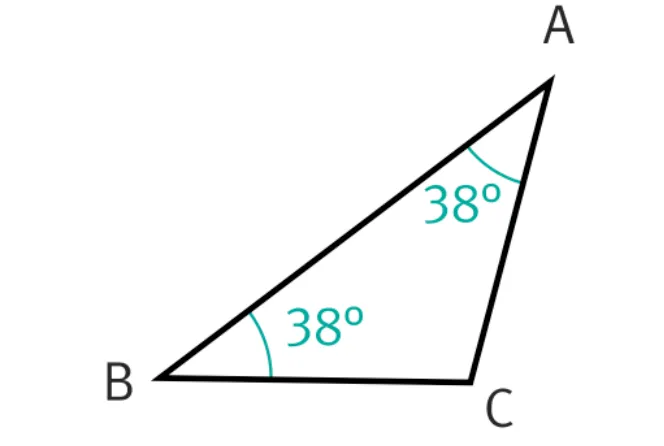
3. Le triangle ABC est-il particulier ? Si oui précisez sa nature.

4. Le triangle CPG est-il particulier ? Si oui précisez sa nature.

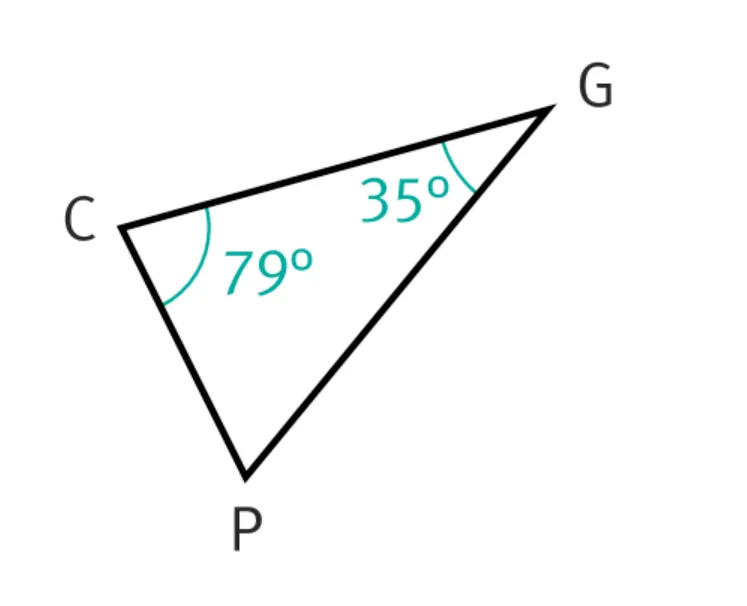


4. Le triangle CPG est-il particulier ? Si oui précisez sa nature.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12 ABCD est un quadrilatère.
✔ Je choisis un cadre adapté (numérique, algébrique ou géométrique) pour traiter un problème

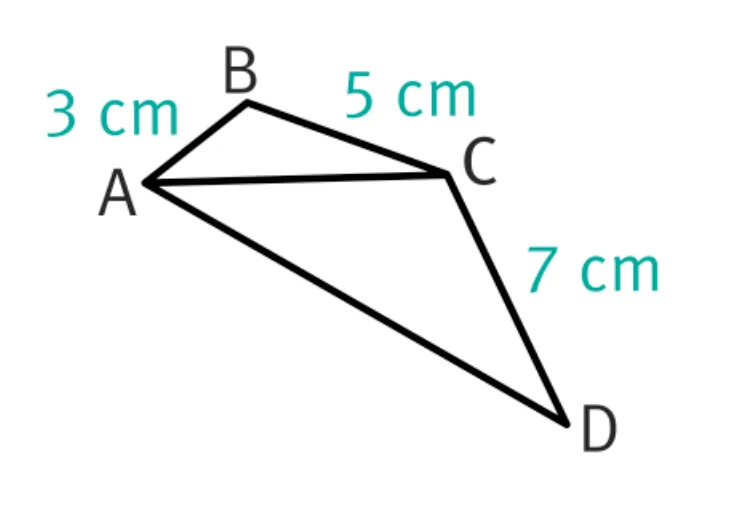


1. Quelle est la longueur minimale et la longueur maximale de [AC] pour que le triangle ABC existe ?
2. On suppose que AC = 6 cm. À quelle condition le triangle ACD existe-t-il ?
2. On suppose que AC = 6 cm. À quelle condition le triangle ACD existe-t-il ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13 Un peu de symétrie centrale.
1. Tracez le triangle ABC tel que BC = 9 cm ; \widehat{\text{ABC}} = 65^{\circ} et \widehat{\text{BCA}} = 39^{\circ}.
2. Construisez les points D et E, symétriques respectifs de B et de C par rapport à A, puis tracez le triangle DAE.
3. Donnez les mesures des angles du triangle AED.
2. Construisez les points D et E, symétriques respectifs de B et de C par rapport à A, puis tracez le triangle DAE.
3. Donnez les mesures des angles du triangle AED.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
14 Angles et nature d'un triangle
✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème
1. Complétez le tableau suivant.
1. Complétez le tableau suivant.
| \widehat{\text{ABC}} | \widehat{\text{ACB}} | \widehat{\text{CAB}} | Nature du triangle ABC |
| 69° |
| 55,5° |
|
| 21° |
|
| Rectangle en C |
|
|
|
| Rectangle isocèle en A |
|
|
| 62° | Isocèle en B |
|
| 17° | 73° |
|
| 24° |
|
| Isocèle en A |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15 Figure
✔ Je représente des objets et des figures géométriques
 1. Reproduisez la figure ci-contre.
1. Reproduisez la figure ci-contre.

Coup de pouce
Commencez par tracer le segment [OE].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16 Tracez le triangle ABD tel que \widehat{\text{ABD}} = 44° ; AD = 2,7 cm et \widehat{\text{BDA}} = 27°.
1. Tracez la droite d, parallèle à (AB) passant par D.
2. Tracez le cercle de centre D et de rayon [BD]. Ce cercle coupe d en E et F.
3. Quelle est la nature des triangles BDE et BDF ? Donnez la mesure de leurs angles.
2. Tracez le cercle de centre D et de rayon [BD]. Ce cercle coupe d en E et F.
3. Quelle est la nature des triangles BDE et BDF ? Donnez la mesure de leurs angles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les droites remarquables d'un triangle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17 Construisez deux triangles RTU tels que RT = 6 cm ; TU = 4,7 cm et RU = 9,5 cm.
1. Tracez alors toutes les hauteurs sur un des triangles et toutes les médiatrices sur lʼautre. Codez les figures réalisées.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
