Mathématiques 6e - 2025
Mes Pages
Rappels de primaire
Chapitre 1
Nombres entiers
Chapitre 2
Notion de fraction
Chapitre 3
Opérations sur les fractions
Chapitre 4
Nombres décimaux
Chapitre 5
Demi-droites graduées
Chapitre 6
Addition, soustraction, multiplication
Chapitre 7
Divisions
Chapitre 8
Organisation et gestion de données
Chapitre 9
Proportionnalité
Chapitre 10
Durées
Chapitre 11
Probabilités
Chapitre 12
Droites et segments
Chapitre 13
Angles
Chapitre 14
Cercles et disques
Chapitre 15
Symétrie axiale
Chapitre 16
Triangles
Chapitre 17
Aires et volumes
Chapitre 4
Entrée en matière
Nombres décimaux
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Histoire des mathsLes notations des nombres décimaux
Les nombres décimaux sont utilisés dans l'histoire depuis des millénaires. On retrouve
des traces d'écritures décimales chinoises au IIe siècle avant notre ère dans Les Neuf
Chapitres sur l'art mathématique. Cependant, l'écriture des nombres décimaux a évolué
au fil du temps pour devenir celle que nous connaissons aujourd'hui.
En 1585, le mathématicien Simon Stevin a proposé une notation novatrice des nombres décimaux : elle facilitait les calculs. Marie Crous, une mathématicienne du XVIIe siècle, a d'ailleurs publié un ouvrage pédagogique basé sur cette notation, proposant même une amélioration. Malgré tout, la notation de Stevin était complexe et elle fut peu utilisée.
À la fin du XVIe siècle, Giovanni Magini propose une notation utilisant un point entre les parties entières et décimales. C'est aujourd'hui la notation des Anglo-Saxons.
Ce sont Willebrord Snell et John Napier qui ont été les premiers à séparer les parties entières et décimales avec une virgule. C'est cette notation qui perdure en France.
En 1585, le mathématicien Simon Stevin a proposé une notation novatrice des nombres décimaux : elle facilitait les calculs. Marie Crous, une mathématicienne du XVIIe siècle, a d'ailleurs publié un ouvrage pédagogique basé sur cette notation, proposant même une amélioration. Malgré tout, la notation de Stevin était complexe et elle fut peu utilisée.
À la fin du XVIe siècle, Giovanni Magini propose une notation utilisant un point entre les parties entières et décimales. C'est aujourd'hui la notation des Anglo-Saxons.
Ce sont Willebrord Snell et John Napier qui ont été les premiers à séparer les parties entières et décimales avec une virgule. C'est cette notation qui perdure en France.
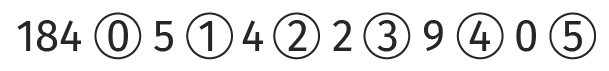
Notation de Simon Stevin du nombre 184,542~90.
Écrire le nombre 45,173 selon la notation de Simon Stevin.
Cliquez ici pour avoir accès à un espace de dessin
Supplément numérique
Retrouvez cette histoire en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les maths à quoi ça sert ?
Dans le monde, il existe environ 160 monnaies différentes : il y a l'euro en France, le
dollar aux États-Unis, le złoty en Pologne, le peso en Argentine, etc. La majorité d'entre
elles s'expriment avec des nombres décimaux dont l'unité principale est subdivisée en
100, d'où le nom de « centimes ».
Par exemple, on a 3~€ = 300 centimes ou bien encore 3,45~€ = 3~€ + 0,45~€ soit 3~€ et 45 centimes.
Par exemple, on a 3~€ = 300 centimes ou bien encore 3,45~€ = 3~€ + 0,45~€ soit 3~€ et 45 centimes.
Pour déposer des pièces d'un centime d'euro à la banque, il faut parfois les
conditionner en rouleaux de 50 pièces. Quelle somme en euros est déposée
si on remplit cinq rouleaux ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité de manipulationDéfinir un nombre décimal
Pour réaliser cette activité, utiliser la .
Pour faire des mesures dans son travail, une bûcheronne s'aide d'un bâton (gabarit n°1) qu'elle reporte sur les choses à mesurer. Ce bâton est donc son unité de mesure.
1. Combien de fois peut-on reporter le bâton sur le tronc ? Quelle est donc la mesure du tronc en nombre de bâtons ?
2. La bûcheronne voudrait mesurer la taille de son fils avec ce même bâton.
a. Peut-elle être aussi précise qu'avec le tronc d'arbre ? Pourquoi ?
Elle décide donc de graduer le bâton en dix segments de même taille.
b. Mesurer le fils avec le bâton gradué (gabarit n°2).
Pour faire des mesures dans son travail, une bûcheronne s'aide d'un bâton (gabarit n°1) qu'elle reporte sur les choses à mesurer. Ce bâton est donc son unité de mesure.
1. Combien de fois peut-on reporter le bâton sur le tronc ? Quelle est donc la mesure du tronc en nombre de bâtons ?
c. Recopier et compléter la phrase: « Le fils mesure \text{\ldots} bâtons entiers et encore \text{\ldots} dixièmes
de bâton que l'on écrit 2+\frac{\text{\ldots}}{10} ou \frac{\text{\ldots}}{10}».
3. La bûcheronne décide maintenant de mesurer l'épaisseur de sa corde. Les dixièmes ne
suffisent plus, elle a alors à nouveau partagé chaque dixième en dix.
a. Quelle fraction du bâton représente chacun des morceaux ainsi obtenus ?
b. Recopier et compléter la phrase :
« L'épaisseur de la corde correspond à cinq morceaux du nouveau découpage, son épaisseur est donc égale à \frac{\text{\ldots}}{\text{\ldots}} de bâton ».
Comment appelle-t-on les fractions dont le dénominateur est égal à 10 ou à 100 ? Comment définir un nombre décimal à partir de ces fractions ?
a. Quelle fraction du bâton représente chacun des morceaux ainsi obtenus ?
« L'épaisseur de la corde correspond à cinq morceaux du nouveau découpage, son épaisseur est donc égale à \frac{\text{\ldots}}{\text{\ldots}} de bâton ».
Bilan
Comment appelle-t-on les fractions dont le dénominateur est égal à 10 ou à 100 ? Comment définir un nombre décimal à partir de ces fractions ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité Comparer des nombres décimaux
Marie, Léana et Apolline vont à la boulangerie
1. Au moment de payer, Marie dit à Léana :
« C'est toi qui as le plus d'argent, c'est toi qui paies ! ».
Marie a-t-elle raison ? Expliquer son raisonnement.
1. Au moment de payer, Marie dit à Léana :
« C'est toi qui as le plus d'argent, c'est toi qui paies ! ».
2. Apolline possède un billet de 10~€. Elle aimerait acheter trois pâtisseries coûtant respectivement 3,75~€, 4,10~€ et 2,95~€.
Que peut-elle faire pour estimer rapidement si son billet de 10~€ sera suffisant ?
Comment comparer deux nombres décimaux ? Comment déterminer un ordre de grandeur d'un nombre décimal?
Que peut-elle faire pour estimer rapidement si son billet de 10~€ sera suffisant ?
Bilan
Comment comparer deux nombres décimaux ? Comment déterminer un ordre de grandeur d'un nombre décimal?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
