Mathématiques 6e - 2025
Mes Pages
Rappels de primaire
Chapitre 1
Nombres entiers
Chapitre 2
Notion de fraction
Chapitre 3
Opérations sur les fractions
Chapitre 4
Nombres décimaux
Chapitre 5
Demi-droites graduées
Chapitre 6
Addition, soustraction, multiplication
Chapitre 7
Divisions
Chapitre 8
Organisation et gestion de données
Chapitre 9
Proportionnalité
Chapitre 10
Durées
Chapitre 11
Probabilités
Chapitre 12
Droites et segments
Chapitre 13
Angles
Chapitre 14
Cercles et disques
Chapitre 15
Symétrie axiale
Chapitre 16
Triangles
Chapitre 17
Aires et volumes
Chapitre 4
Cours
Nombres décimaux
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Définitions et différentes écritures
Définition
Un nombre décimal est un nombre qui peut s'écrire sous la forme d'une fraction décimale, c'est-à-dire une fraction dont le numérateur est un nombre entier et le dénominateur est 1, 10, 100, 1~000, etc.
Exemples :
1. Le nombre \frac{3~487}{1~000} est un nombre décimal : le numérateur est le nombre entier 3 487 et le dénominateur est 1~000.
2. Le nombre entier 35 est aussi un nombre décimal car 35=35 \div 1=\frac{35}{1}.
3. Le pourcentage 72~\% est un nombre décimal car 72~\% = \frac{72}{100}.
1. Le nombre \frac{3~487}{1~000} est un nombre décimal : le numérateur est le nombre entier 3 487 et le dénominateur est 1~000.
2. Le nombre entier 35 est aussi un nombre décimal car 35=35 \div 1=\frac{35}{1}.
3. Le pourcentage 72~\% est un nombre décimal car 72~\% = \frac{72}{100}.
Définition
Lorsqu'un nombre décimal est écrit comme un nombre mixte, l'entier est la partie entière et la fraction décimale inférieure à 1 est la partie décimale.
Exemple :
Le nombre décimal \frac{69~481}{100} s'écrit sous forme d'un nombre mixte
\frac{69~400}{100} + \frac{81}{100} = 694 + \frac{81}{100} donc 694 est la partie entière et \frac{81}{100} est la partie décimale.
Pour finir, puisque \frac{81}{100} = 81 \div 100 = 0,81, on a alors \frac{69~481}{100} = 694 + 0,81 = 694,81.
Le nombre décimal \frac{69~481}{100} s'écrit sous forme d'un nombre mixte
\frac{69~400}{100} + \frac{81}{100} = 694 + \frac{81}{100} donc 694 est la partie entière et \frac{81}{100} est la partie décimale.
Pour finir, puisque \frac{81}{100} = 81 \div 100 = 0,81, on a alors \frac{69~481}{100} = 694 + 0,81 = 694,81.
- Remarque : Certains nombres ne peuvent pas s'écrire sous forme de fraction décimale. Ce ne sont donc pas des nombres décimaux. C'est le cas, par exemple, du nombre \frac{1}{3} et du nombre \pi. Ils possèdent une infinité de chiffres après la virgule.
Propriété
Un nombre décimal admet différentes décompositions.
Exemple :
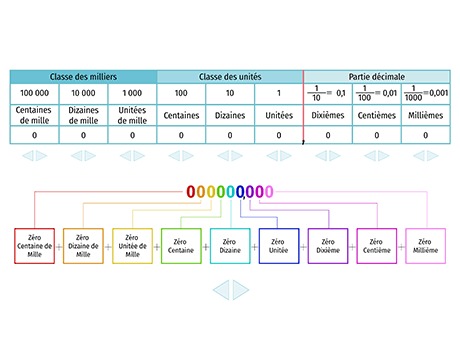
Voici différentes façons de décomposer le nombre 694,81 en s'aidant du tableau
Voici différentes façons de décomposer le nombre 694,81 en s'aidant du tableau
- Remarques : Dans 694,81 : le chiffre 9 est le chiffre des dizaines mais 69 est le nombre de dizaines car 694,81=69 \times 10+4,81 . De même, puisque 694,81=6~948 \times 0,1+0,01 alors 6~948 est le nombre de dixièmes alors que le chiffre de dixièmes est 8.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Comparaison et arrondis
Methode
Pour comparer deux nombres décimaux, on compare d'abord leur partie entière :
- si elles sont différentes, alors le nombre le plus grand est celui qui a la plus grande partie entière ;
- si elles sont égales, on compare les décimales de chaque nombre en commençant par le chiffre des dixièmes, puis celui des centièmes, etc. On peut ajouter des zéros inutiles si besoin.
Exemples :
1. Comparons 13,79 et 11,21. Puisque 13>11 alors 13,79 > 11,21.
2. Comparons 11,2 et 11,201. Les parties entières de 11,2 et 11,201 sont égales. On remarque que 11,2 = 11,200, on va donc comparer 11,{\color{red}2}{\color{blue}0}{\color{green}0} et 11,{\color{red}2}{\color{blue}0}{\color{green}1}. Le chiffre des dixièmes est {\color{red}2} pour ces deux nombres. Le chiffre des centièmes est {\color{blue}0} pour ces deux nombres. Le chiffre des millièmes est différent et {\color{green}0} < {\color{green}1}. On conclut donc que 11,2< 11,201.
1. Comparons 13,79 et 11,21. Puisque 13>11 alors 13,79 > 11,21.
2. Comparons 11,2 et 11,201. Les parties entières de 11,2 et 11,201 sont égales. On remarque que 11,2 = 11,200, on va donc comparer 11,{\color{red}2}{\color{blue}0}{\color{green}0} et 11,{\color{red}2}{\color{blue}0}{\color{green}1}. Le chiffre des dixièmes est {\color{red}2} pour ces deux nombres. Le chiffre des centièmes est {\color{blue}0} pour ces deux nombres. Le chiffre des millièmes est différent et {\color{green}0} < {\color{green}1}. On conclut donc que 11,2< 11,201.
Définition
Arrondir un nombre à un rang donné, c'est trouver le nombre le plus proche du nombre initial dont l'écriture s'arrête à ce rang. On utilise le symbole « environ égal » \approx entre le nombre et son arrondi.
Exemples :
1. L'arrondi à l'unité de 23,7 est 24 : c'est le nombre entier le plus proche de celui-ci. On note 23,7 \approx 24.
2. L'arrondi au dixième de 91,42 est 91,4 : c'est le nombre décimal le plus proche de 91,42 au dixième près. On note 91,42 \approx 91,4.
3. L'arrondi au millième de \frac{1}{3} est 0,333. On note alors \frac{1}{3} \approx 0,333.
4. L'arrondi au centième de \pi est 3,14. On note \pi \approx 3,14.
1. L'arrondi à l'unité de 23,7 est 24 : c'est le nombre entier le plus proche de celui-ci. On note 23,7 \approx 24.
2. L'arrondi au dixième de 91,42 est 91,4 : c'est le nombre décimal le plus proche de 91,42 au dixième près. On note 91,42 \approx 91,4.
3. L'arrondi au millième de \frac{1}{3} est 0,333. On note alors \frac{1}{3} \approx 0,333.
4. L'arrondi au centième de \pi est 3,14. On note \pi \approx 3,14.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
