Chapitre 13
Entraînement
Angles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Angles particuliers
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17
À l'oral
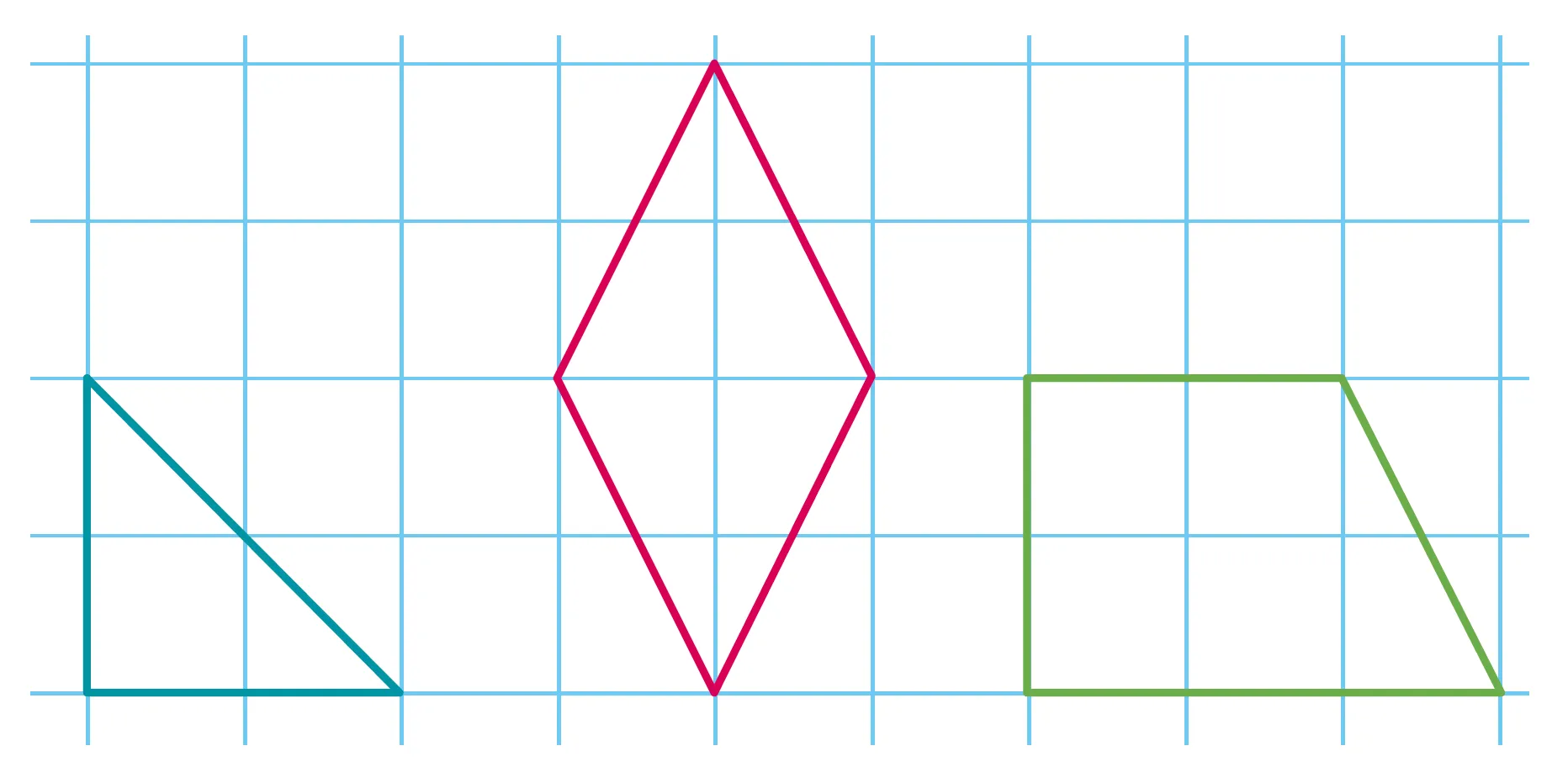
Décrire chaque figure en précisant
combien elle possède d'angles aigus,
droits et obtus.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18
Décrire les figures suivantes en précisant combien elles possèdent d'angles aigus, droits et obtus : un carré, un rectangle et un triangle rectangle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19À l'oral
À l'oral
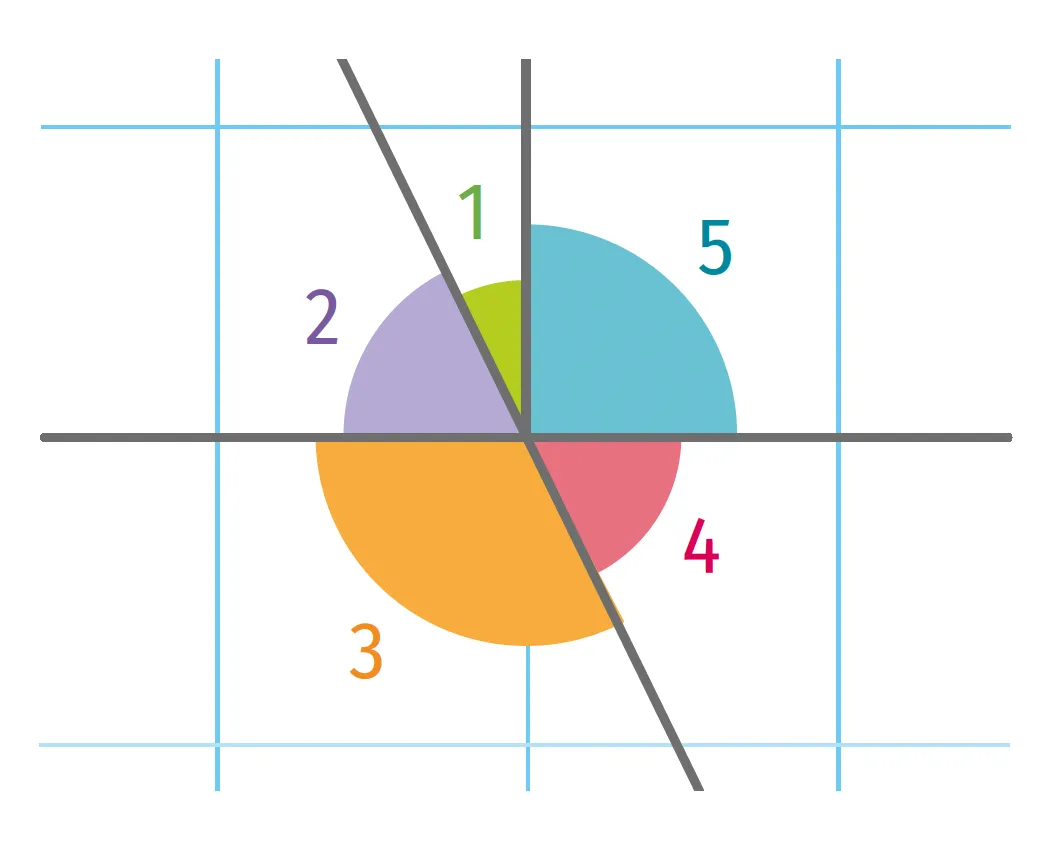
Identifier
les angles
aigus, droits
et obtus de
cette figure.
Expliquer le
raisonnement.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20
Sur la figure ci-dessous, quels angles
semblent être aigus ? Droits ? Obtus ? Après
avoir répondu, vérifier à l'aide d'une équerre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21
Sur la figure ci-dessous,
quels angles semblent
être aigus ? Droits ?
Obtus ? Après avoir
répondu, vérifier à l'aide
d'une équerre.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22
Construire des quadrilatères ayant :
1. deux angles droits consécutifs (qui se suivent), un angle aigu et un obtus ;
2. trois angles obtus dont deux égaux et un aigu.
1. deux angles droits consécutifs (qui se suivent), un angle aigu et un obtus ;
2. trois angles obtus dont deux égaux et un aigu.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
À 10~\text{h}~12, les aiguilles d'une horloge
forment un angle obtus. Donner des
exemples d'heures où elles forment un
autre angle obtus, un droit, un aigu, un nul
et un plat.




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
On partage un angle obtus en deux
angles égaux. Les angles obtenus peuvent-ils être obtus ? Égaux à un angle droit ?
Expliquer le raisonnement.
Expliquer le raisonnement.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
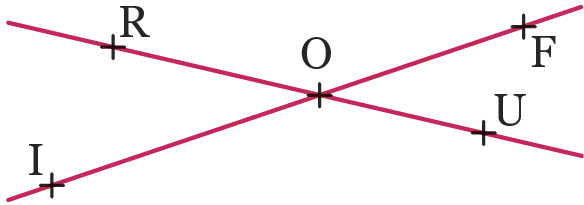
25
Nommer les angles aigus formés par
les droites\text { (RU) }et\text { (FI) }ci-dessous.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
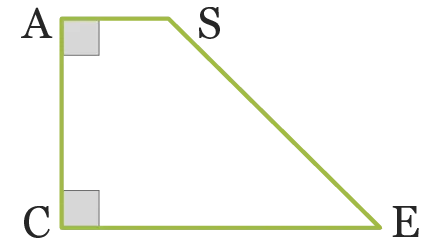
26
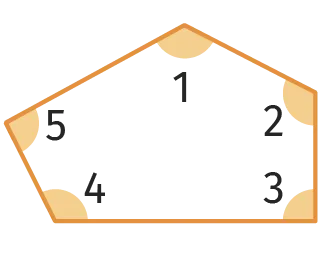
Nommer les
angles de ce trapèze
en précisant leur
nature.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
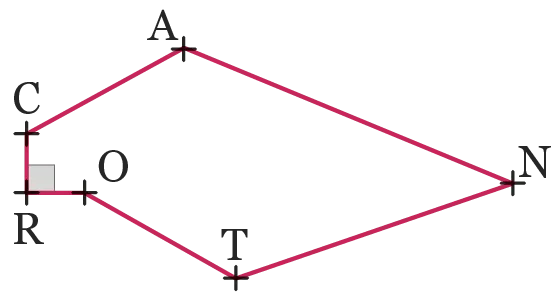
27
Donner la nature des angles du
polygone\text { CANTOR} ci-dessous.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28
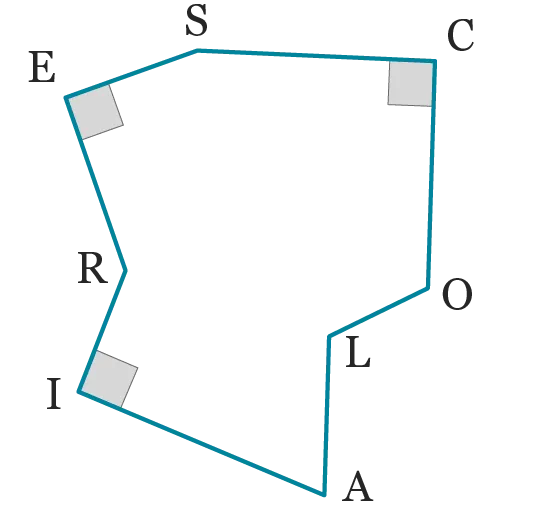
Donner
la nature
des angles
du polygone
\text {SCOLAIRE} ci-
dessous.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29
Copie d'élève
On considère la figure ci-dessous.

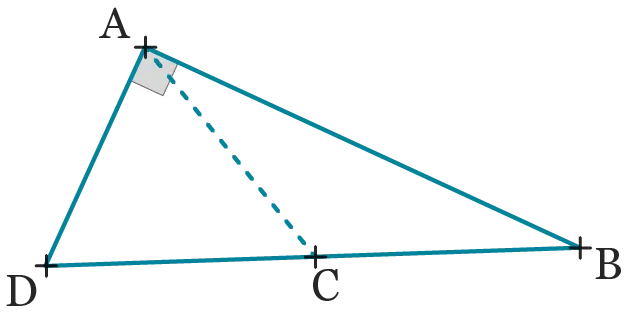
On souhaite connaître la nature des angles
que l'on peut définir avec \text{A} et \text{C}.
Corriger la copie d'Eli ci-dessous.


Corriger la copie d'Eli ci-dessous.
Les angles \widehat{\mathrm{ADC}}, \widehat{\mathrm{DCA}} et \widehat{\mathrm{CAD}} sont obtus.
L'angle \widehat{\mathrm{ACB}} est aigu
L'angle \widehat{\mathrm{ACB}} est aigu
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30
Construire un quadrilatère \text {MATH}
respectant le schéma à main levée ci-dessous.

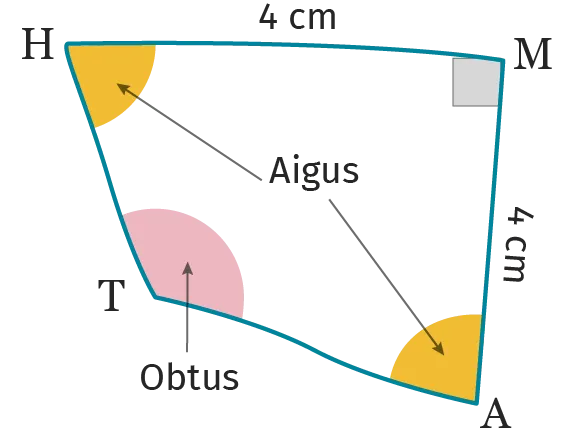


Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31
En s'aidant d'un schéma à main levée,
construire un quadrilatère \text {HALO} tel que
\widehat{\mathrm{OLA}} et \widehat{\mathrm{HOL}} soient aigus et \widehat{\mathrm{OHA}} soit droit.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32
Tracer un polygone \text {CROUS} ayant deux
angles droits, deux angles obtus et un angle
aigu.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33
Compléter les phrases suivantes.
1. Deux angles sont adjacents lorsque.
2. Deux angles ont leur sommet en commun et leurs côtés sont le prolongement l'un de
l'autre.
3. Deux angles supplémentaires forment un à eux deux.
1. Deux angles sont adjacents lorsque
2. Deux angles
3. Deux angles supplémentaires forment un
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
34
Générateur d'exercices
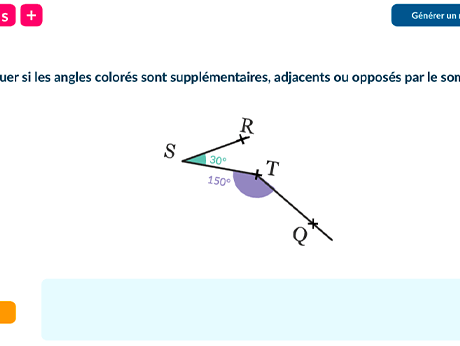
Dans chaque cas, indiquer si les angles
colorés sont supplémentaires, adjacents ou
opposés par le sommet.
1.

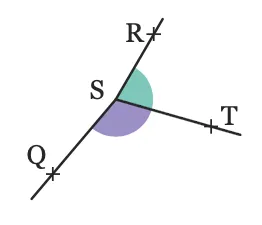 2.
2.

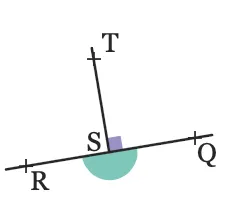




3.

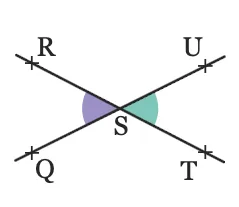 4.
4.





Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35
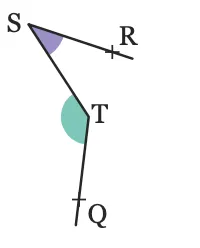
On modélise les boucles d'un nœud par
la figure ci-dessous.


En utilisant les points de la figure, indiquer les angles adjacents, supplémentaires et opposés par le sommet.


En utilisant les points de la figure, indiquer les angles adjacents, supplémentaires et opposés par le sommet.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
36
On considère les figures ci-dessous.

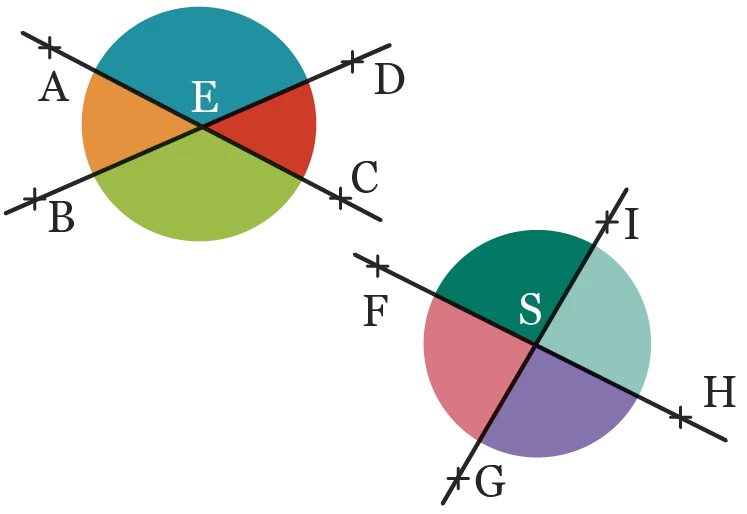 Donner :
Donner :
1. deux paires d'angles supplémentaires ;
2. deux paires d'angles adjacents ;
3. deux paires d'angles opposés par le
sommet.

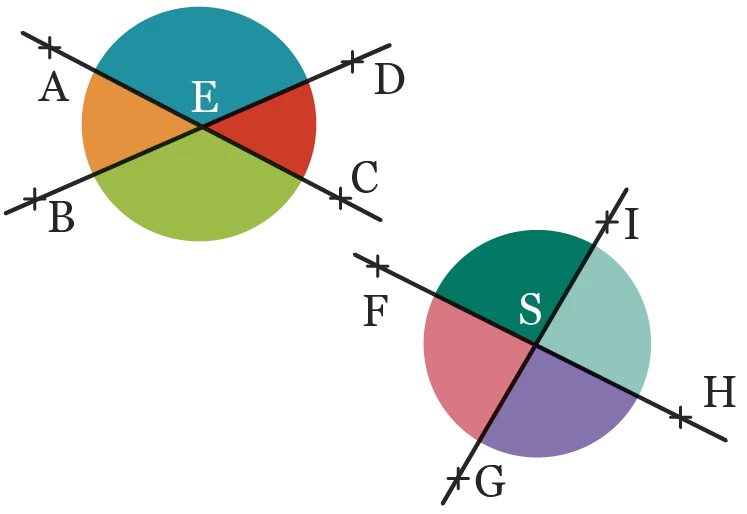
1. deux paires d'angles supplémentaires ;
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
37
Dans chaque cas, réaliser la figure
demandée.
1. Tracer deux angles opposés par le sommet.
2. Tracer deux angles supplémentaires adjacents.
3. Tracer deux angles adjacents qui ne soient pas supplémentaires.
1. Tracer deux angles opposés par le sommet.
2. Tracer deux angles supplémentaires adjacents.
3. Tracer deux angles adjacents qui ne soient pas supplémentaires.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
38
Sur la figure suivante, \text {A} est le point
d'intersection de \text {(EC)} , \text {(GD)} et \text {(BF)} .

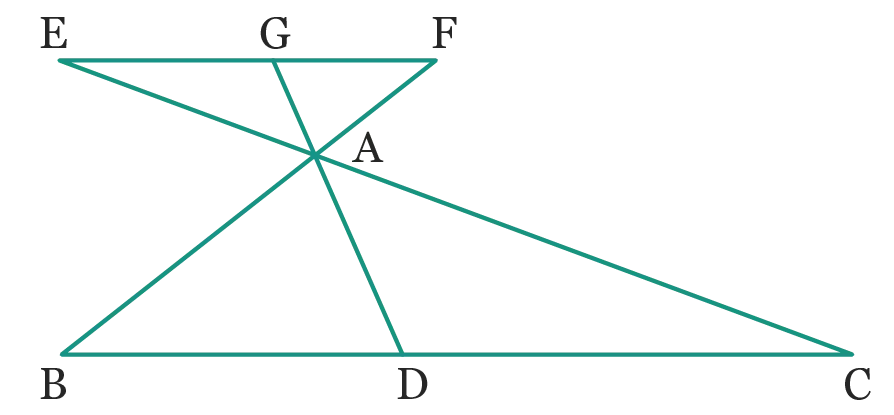 1. Donner cinq paires d'angles adjacents.
2. Donner toutes les paires d'angles opposés
par le sommet.
1. Donner cinq paires d'angles adjacents.
2. Donner toutes les paires d'angles opposés
par le sommet.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Mesure en degré d'un angle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
39
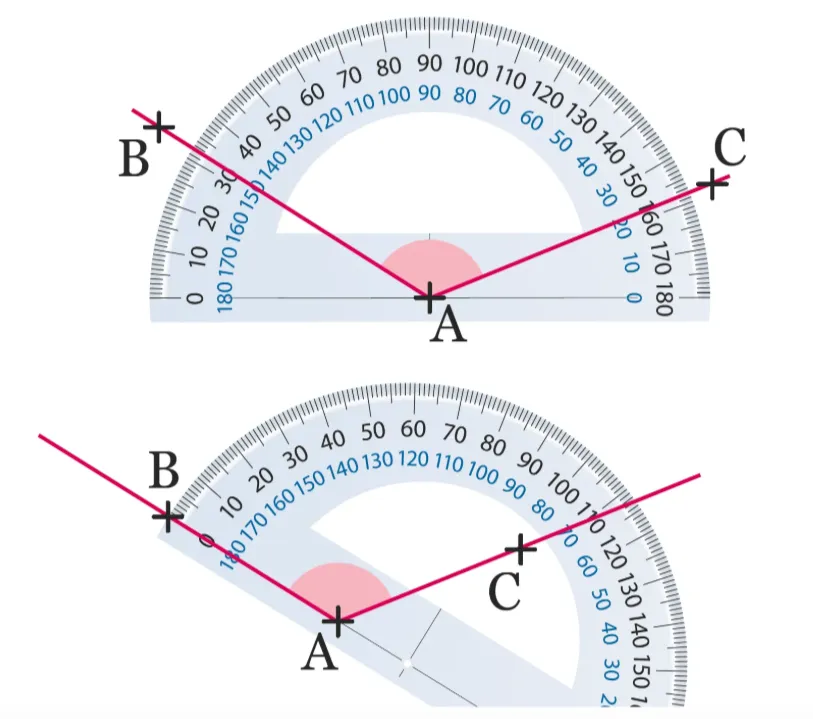
À l'oral
Dans chaque cas, pourquoi le rapporteur est-il mal positionné pour lire la mesure de l'angle \widehat{\mathrm{BAC}} ?



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
40À l'oral
À l'oral
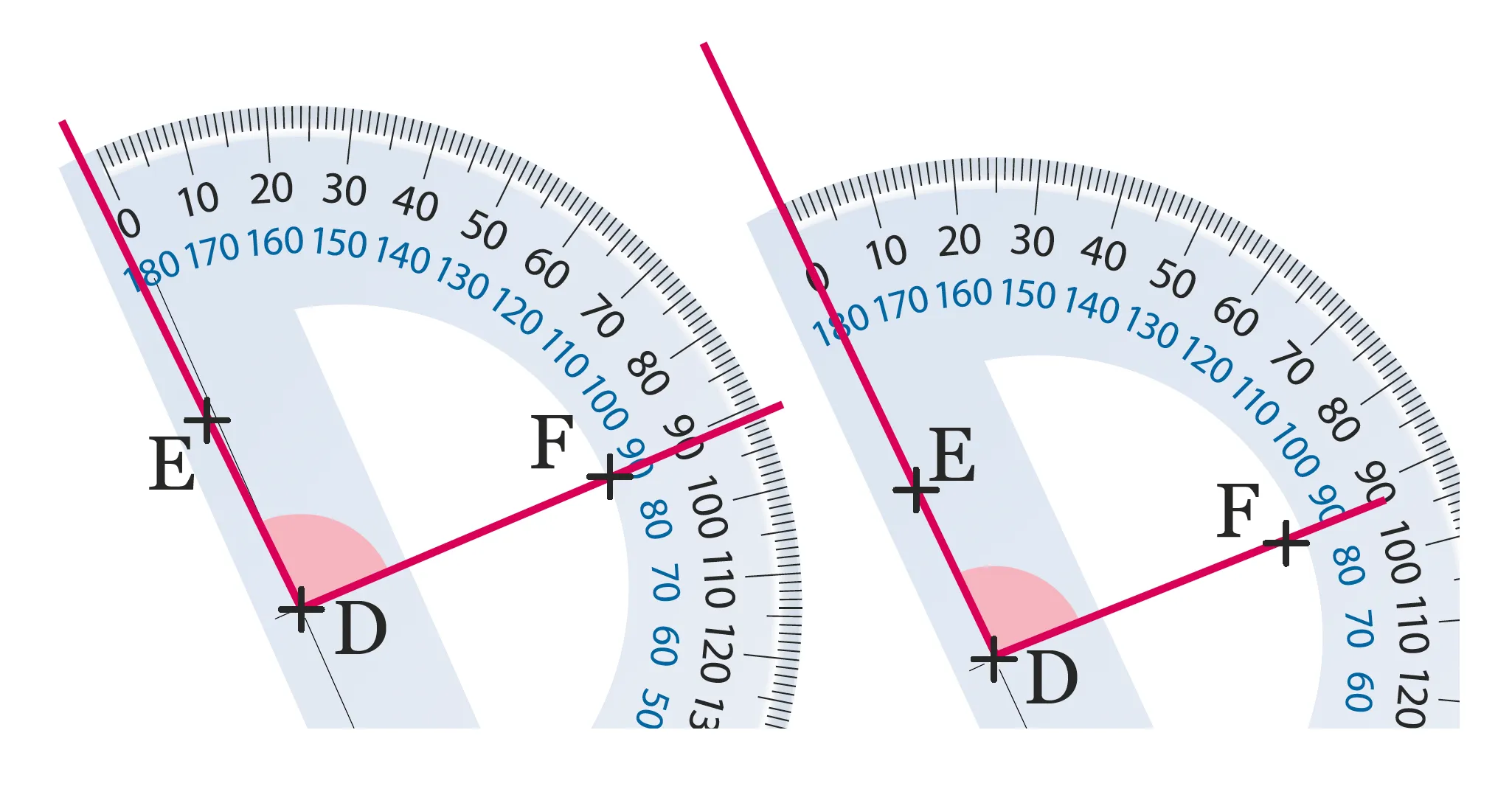
Dans chaque cas, que faut-il corriger
pour bien lire la mesure de l'angle \widehat{\mathrm{EDF}} ?



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
41À l'oral
À l'oral
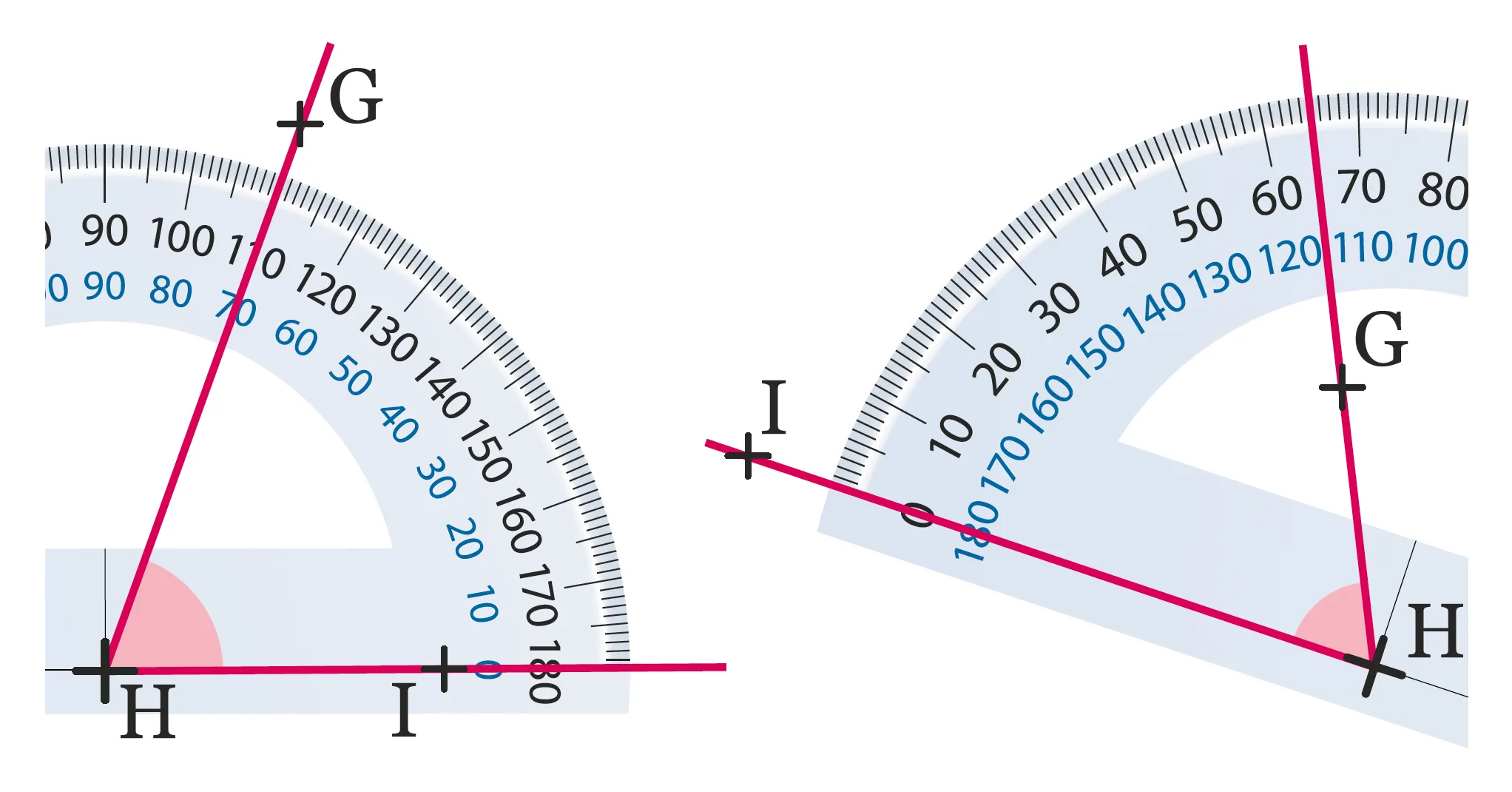
Dans chaque cas, le rapporteur est
bien positionné. Lire la mesure de l'angle
\widehat{\mathrm{GHI}}.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
42
TICE
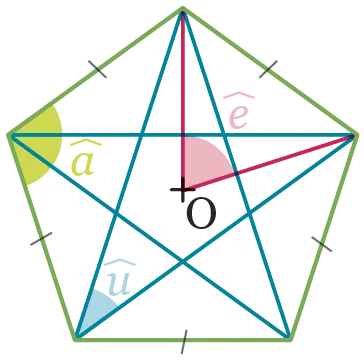
Le point \text {O} est le
centre d'un pentagone
régulier.
Reproduire la figure sur
GeoGebra et afficher la
mesure des angles \hat{u},
\hat{a} et \hat{e}. Que remarque-t-on ?



Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour les exercices 43 à 46, les figures
sont à .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
43
On considère le parallélogramme \text {KEBI}
ci-dessous.




1. Mesurer ses quatre angles.
2. Quelles remarques peut-on faire ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
44
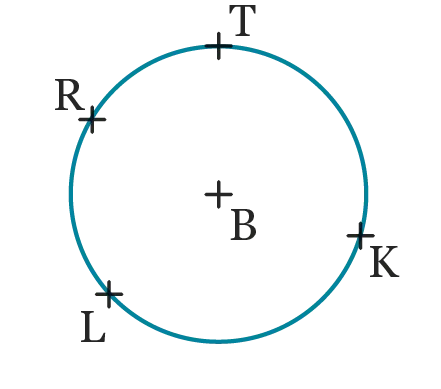
Les points
\text {K} , \text {L} , \text {R} et \text {T}
appartiennent au
cercle de centre \text {B}
ci-dessous.

3. Construire un cercle de centre \text {A} et de
rayon 5\mathrm{~cm}. Placer trois points \text {G}, \text {H} et \text {J} sur
ce cercle et mesurer les angles \widehat{\text {GAH}} et \widehat{\text {GJH}}.
Que remarque-t-on ?
1. Mesurer les angles \widehat{\text {RLT}} et \widehat{\text {RKT}}. Que
remarque-t-on ?
2. Mesurer l'angle \widehat{\text {RBT}}. Que remarque-t-on ?


Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
45
Copie d'élève
En mesurant les angles apparaissant
sur la constellation de la Grande Ourse, Léo
a fait trois erreurs.

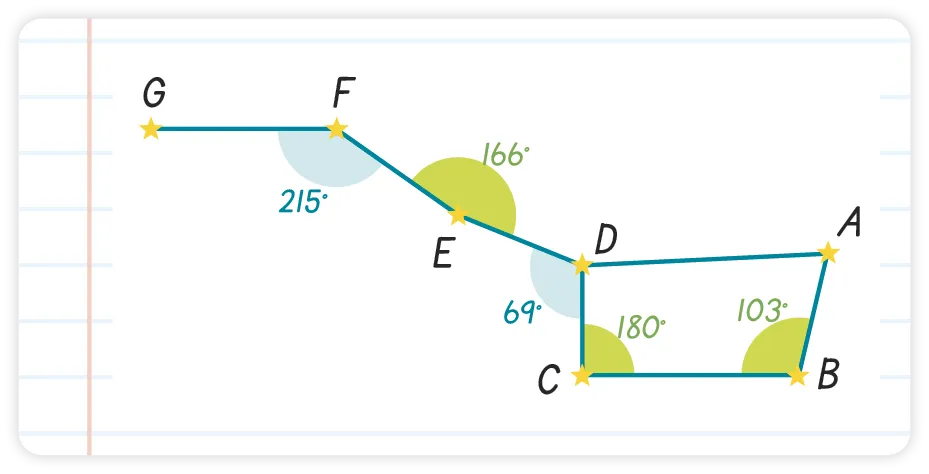
Les identifier sans mesurer, puis les corriger.


Les identifier sans mesurer, puis les corriger.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46
Copie d'élève
En mesurant les angles apparaissant
sur la constellation de la Petite Ourse, Nami
a fait trois erreurs.

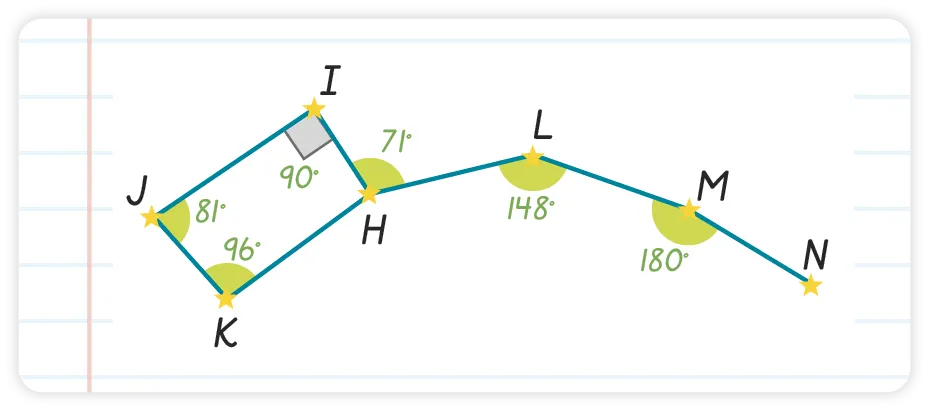
Les identifier sans mesurer, puis les corriger.


Les identifier sans mesurer, puis les corriger.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
47
La constellation de Cassiopée est
constituée de cinq étoiles formant un \text {W} .
Placer deux étoiles \text {A} et \text {B} à 4~\mathrm{cm} l'une de
l'autre à l'horizontale. Placer les étoiles
restantes.
L'étoile \text {C} est à 4~\mathrm{cm} de \text {B} et \widehat{\mathrm{ABC}}=130^{\circ}.
L'étoile \text {D} est à 4~\mathrm{cm} de \text {C} et \widehat{\mathrm{BCD}}=120^{\circ}.
Enfin, l'étoile \text {E} est à 4~\mathrm{cm} de \text {D} et \widehat{\mathrm{CDE}}=80^{\circ}.
L'étoile \text {C} est à 4~\mathrm{cm} de \text {B} et \widehat{\mathrm{ABC}}=130^{\circ}.
L'étoile \text {D} est à 4~\mathrm{cm} de \text {C} et \widehat{\mathrm{BCD}}=120^{\circ}.
Enfin, l'étoile \text {E} est à 4~\mathrm{cm} de \text {D} et \widehat{\mathrm{CDE}}=80^{\circ}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48
Construire un polygone régulier de
côté 3~ \mathrm{cm} et dont les angles aux sommets
mesurent tous 135^\circ. Combien a-t-il de côtés ?
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49
J'ai mangé un sixième d'une pizza
circulaire puis un quart et enfin un huitième.
Calculer la mesure de l'angle correspondant
à la part que j'ai mangé.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
50
Reproduire la figure ci-dessous en
utilisant les mesures indiquées.
Calculer la mesure du dernier angle.

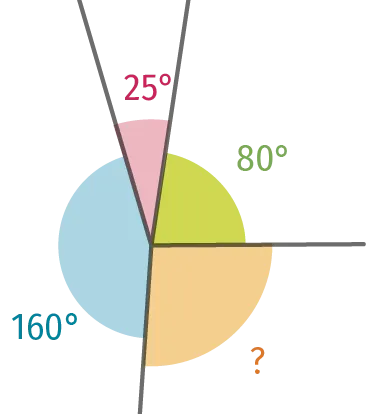

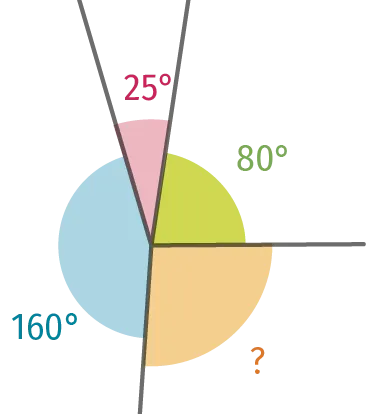
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
51
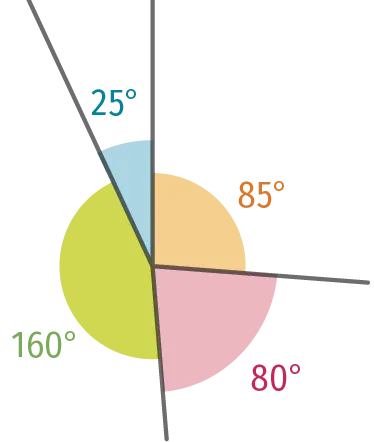
Expliquer pourquoi la figure
schématisée ci-dessous est impossible à
reproduire avec les mesures indiquées.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
52Copie d'élève
Copie d'élève
Voici une figure à main levée donnée
lors d'une évaluation. On demande si les
points \text {P} , \text {O} et \text {T} sont alignés.

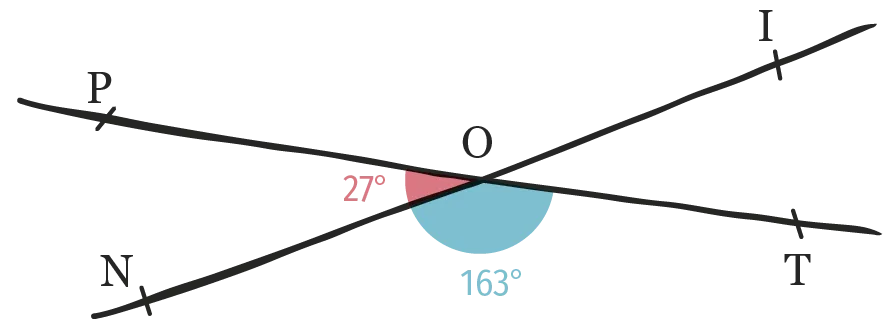
Voici la copie de Gabin.


Voici la copie de Gabin.
27+163=180. On peut donc en déduire
que \widehat{\text {POT}} forme un angle nul.
Les points \text {P} , \text {O} et \text {T} sont donc alignés.
Relire chaque étape de son raisonnement en
corrigeant les éventuelles erreurs.Les points \text {P} , \text {O} et \text {T} sont donc alignés.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
53
Une patte d'un
ornithorynque est
constituée de cinq
doigts qui mesurent
chacun 3,5~\mathrm{cm}.
Ouverte, la patte forme un angle de 125^{\circ} entre ses doigts de gauche et de droite.
Elle est partagée en deux angles de 25^{\circ} aux extrémités. Un des angles intérieurs mesure 35^{\circ}. 1. À l'aide du calcul, déterminer la mesure de l'angle restant.
2. Tracer le schéma de la patte en vraie
grandeur.
Ouverte, la patte forme un angle de 125^{\circ} entre ses doigts de gauche et de droite.
Elle est partagée en deux angles de 25^{\circ} aux extrémités. Un des angles intérieurs mesure 35^{\circ}. 1. À l'aide du calcul, déterminer la mesure de l'angle restant.
Cliquez pour accéder à GeoGebra


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
54
Exercice inversé
Écrire un énoncé d'exercice
dont la réponse pourrait être :
« 155 + 25 = 180.
Les points \text {B} , \text {O} et \text {P} sont donc alignés. »
« 155 + 25 = 180.
Les points \text {B} , \text {O} et \text {P} sont donc alignés. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
55
Générateur d'exercices
Générateur d'exercices

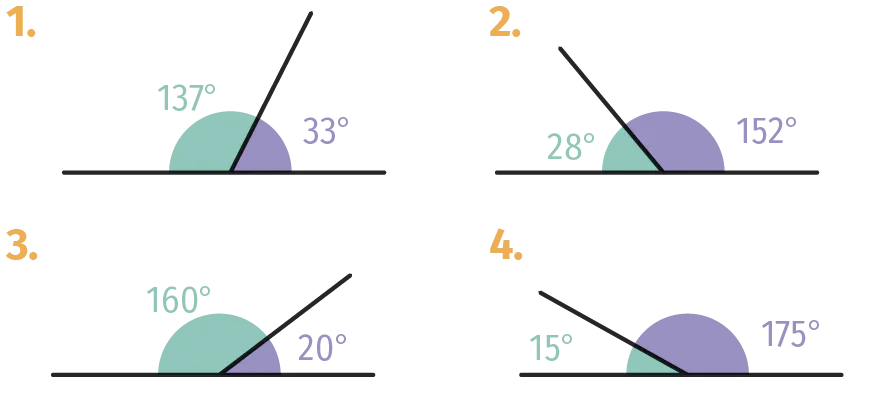
Dans chaque cas, déterminer en justifiant si la figure est correcte.
Figure 1
Figure 2
Figure 3
Figure 4
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
56

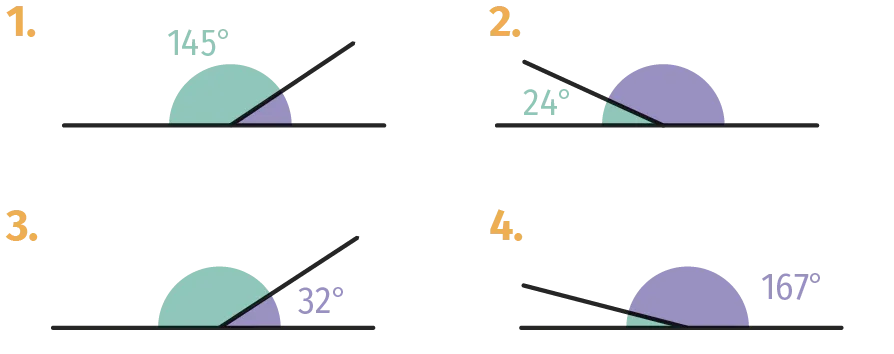
Pour chaque paire d'angles, calculer la mesure de l'angle supplémentaire :
Figure 1
Figure 2
Figure 3
Figure 4
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
57
Environnement
Environnement
On considère le tableau
suivant consignant les secteurs
d'émission de gaz à effet de serre
des Français. Chaque secteur est associé
à un angle : plus l'angle est grand, plus
les émissions du secteur sont
importantes.
1. Construire le diagramme circulaire correspondant.
2. Mesurer la valeur de l'angle correspondant à l'habitat. Comment retrouver cette mesure par le calcul ?
3. Quel est le secteur le plus émetteur de gaz à effet de serre ? Justifier.
| Secteur | Angle |
|---|---|
| Déplacement | 135^{\circ} |
| Équipement | 42^{\circ} |
| Alimentation | 88^{\circ} |
| Habitat | ? |
1. Construire le diagramme circulaire correspondant.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
58
Riley affirme que la bissectrice d'un angle plat forme des angles droits. A‑t-elle raison ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
59
Pour chaque paire d'angles opposés
par le sommet, déterminer la mesure
manquante.

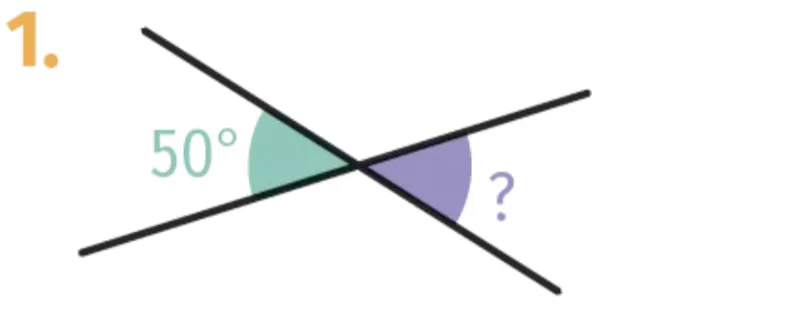 1.
1.

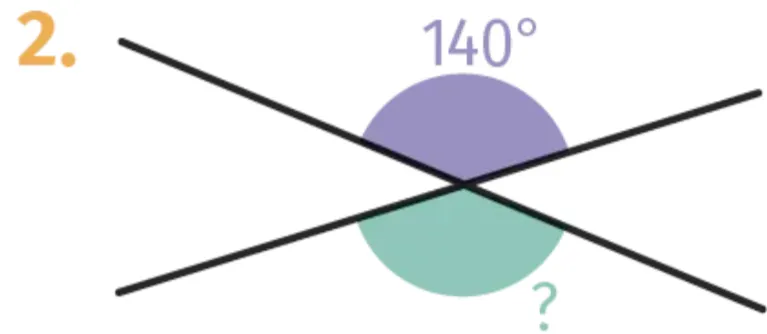 2.
2.




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
60
Dans la figure ci-dessous, le point \text {E} est
Le point d'intersection des droites \text {(IB)} , \text {(JL)}
et \text {(DK)} .

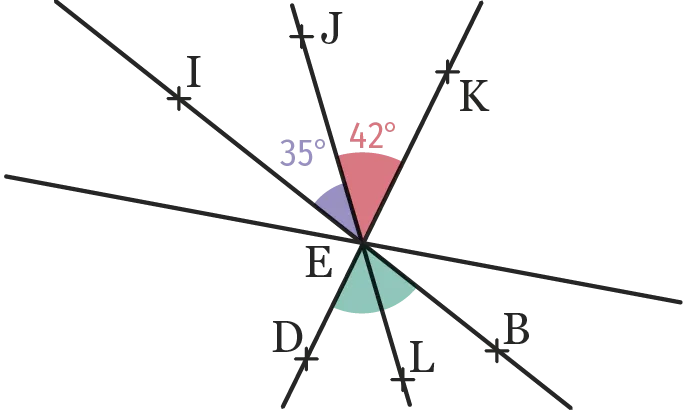
Calculer la mesure de l'angle \widehat{\text {BED}}.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
61
Dans chaque cas, dire si la demi-droite\text { [OB) }est la bissectrice de l'angle \widehat{\mathrm{AOC}}.
Justifier.
Figure 1
Figure 2
Figure 3
Figure 4

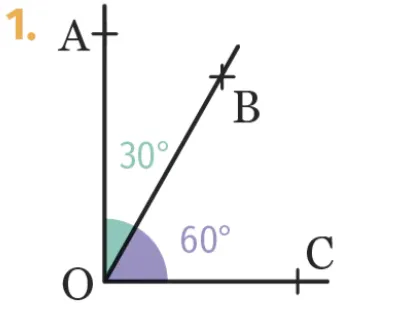

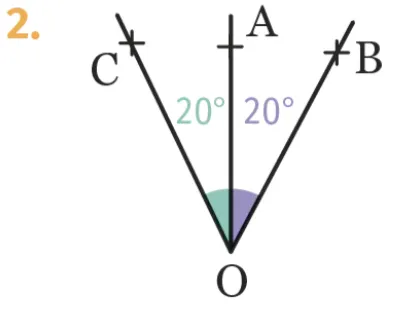

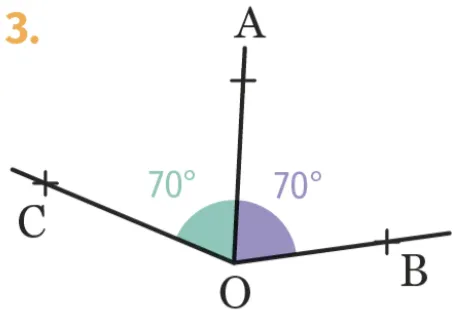

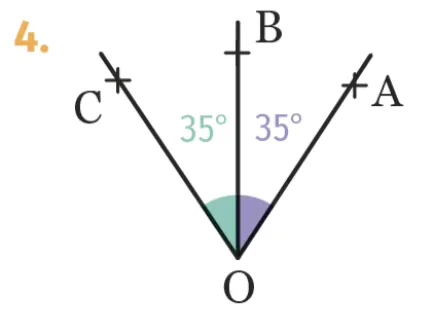
Figure 1








Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
62
Reproduire les angles suivants et tracer leur bissectrice.

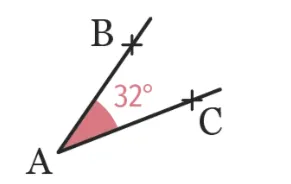

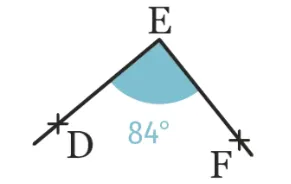

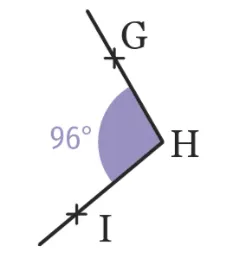









Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
63
Tracer les angles suivants, puis tracer
leur bissectrice.
1. \widehat{\mathrm{COU}}=100^{\circ}
2. \widehat{\mathrm{MAI}}=26^{\circ}
2. \widehat{\mathrm{MAI}}=26^{\circ}
3. \widehat{\mathrm{DUO}}=86^{\circ}
4. \widehat{\mathrm{VAL}}=154^{\circ}
4. \widehat{\mathrm{VAL}}=154^{\circ}
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
64
On considère un angle \widehat{\mathrm{SPA}} pour lequel
on a tracé sa bissectrice \text {[PR)}.
Calculer la mesure de l'angle \widehat{\mathrm{SPA}} dans les cas suivants.
Calculer la mesure de l'angle \widehat{\mathrm{SPA}} dans les cas suivants.
1.
\widehat{\mathrm{SPR}}=30^{\circ}
2.
\widehat{\mathrm{RPA}}=45^{\circ}
3.
\widehat{\mathrm{APR}}=76^{\circ}
4.
\widehat{\mathrm{APS}}=28^{\circ}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
65
On considère un angle \widehat{\mathrm{QUI}} pour lequel
on a tracé sa bissectrice \text {[UE)}.
Calculer la mesure de l'angle \widehat{\mathrm{QUE}} dans les cas suivants.
1. \widehat{\mathrm{QUI}}=80^{\circ}
2.
\widehat{\mathrm{IUQ}}=29^{\circ}
3.
\widehat{\mathrm{IUE}}=58^{\circ}
Calculer la mesure de l'angle \widehat{\mathrm{QUE}} dans les cas suivants.
1. \widehat{\mathrm{QUI}}=80^{\circ}
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille