Chapitre 13
Synthèse
Angles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
66
TICE
Si on double la taille d'un angle aigu en
le reproduisant par symétrie axiale le long
d'un de ses côtés, pour quelles valeurs de
l'angle de départ l'angle obtenu est-il obtus ?
Aigu ? Égal à l'angle droit ? Expérimenter à
l'aide de GeoGebra et expliquer la démarche.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
67
La spirale d'Archimède est définie comme
le trajet d'une fourmi qui avance à vitesse
constante sur la grande aiguille d'une
horloge.
1. Tracer un disque de rayon 6~\mathrm{cm}.
2. Diviser le disque en douze secteurs
angulaires égaux. Quelle est leur mesure ?
3. La fourmi part du centre à midi et avance
sur l'aiguille de 0,5~\mathrm{cm} par heure. Placer sur
chaque rayon le point correspondant à la
position de la fourmi à l'heure indiquée.
4. Relier ces points à main levée par une courbe. Où se trouve la fourmi à 23 heures ?
1. Tracer un disque de rayon 6~\mathrm{cm}.
Cliquez pour accéder à GeoGebra
4. Relier ces points à main levée par une courbe. Où se trouve la fourmi à 23 heures ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
68
Pour cacher son trésor, une pirate est partie
d'un arbre, a marché sept pas dans la
direction nord-est, puis cinq pas dans la
direction nord-ouest et enfin dix pas vers
sud.
1. Construire un plan de son trajet à l'échelle 1~\mathrm{cm} = 1 pas en partant d'un point \text {A} .
2. Dans quelle direction doit-elle partir depuis le point \text {A} pour retrouver son trésor en ligne droite ? Combien de pas doit-elle faire enviroח ?
1. Construire un plan de son trajet à l'échelle 1~\mathrm{cm} = 1 pas en partant d'un point \text {A} .
2. Dans quelle direction doit-elle partir depuis le point \text {A} pour retrouver son trésor en ligne droite ? Combien de pas doit-elle faire enviroח ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
69
Il ne reste qu'une part de mon gâteau !
Combien de parts égales y avait-il ?
Combien de parts égales y avait-il ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
70
On considère l'angle suivant.

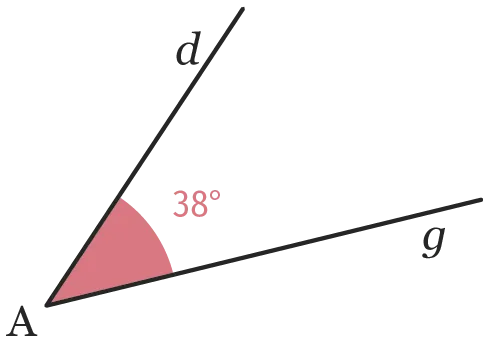
1. Reproduire cet angle en vraie grandeur.
2. Construire la demi-droite [\mathrm{A} x) telle que les angles \widehat{d \mathrm{A}g} et \widehat{g\mathrm{A}x} soient supplémentaires.
3. Construire la demi-droite [\mathrm{A} y) telle que les angles \widehat{g\mathrm{A}x} et \widehat{x\mathrm{A}y} soient supplémentaires.
4. Que peut-on dire des angles \widehat{x\mathrm{A}d} et \widehat{y\mathrm{A}g} ? Justifier.


1. Reproduire cet angle en vraie grandeur.
2. Construire la demi-droite [\mathrm{A} x) telle que les angles \widehat{d \mathrm{A}g} et \widehat{g\mathrm{A}x} soient supplémentaires.
3. Construire la demi-droite [\mathrm{A} y) telle que les angles \widehat{g\mathrm{A}x} et \widehat{x\mathrm{A}y} soient supplémentaires.
Cliquez pour accéder à GeoGebra
4. Que peut-on dire des angles \widehat{x\mathrm{A}d} et \widehat{y\mathrm{A}g} ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
71
On considère la figure suivante.

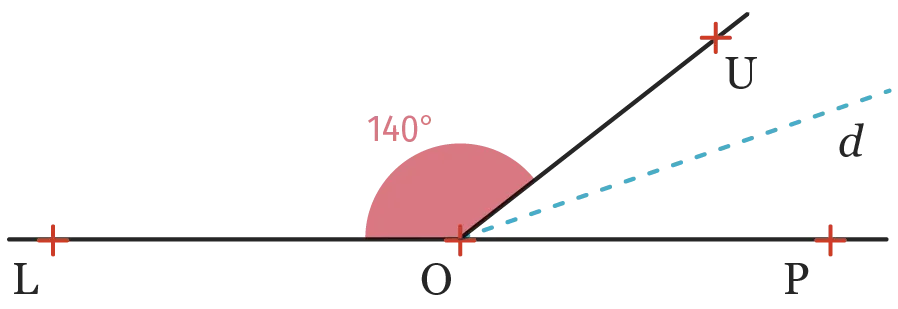
Les points \text {L} , \text {O} et \text {P} sont alignés. La demi-droite {d} est la bissectrice de l'angle \widehat{\mathrm{POU}}.
Quelle est la mesure de l'angle \widehat{ \mathrm{LO}d} ?


Les points \text {L} , \text {O} et \text {P} sont alignés. La demi-droite {d} est la bissectrice de l'angle \widehat{\mathrm{POU}}.
Quelle est la mesure de l'angle \widehat{ \mathrm{LO}d} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
72
1. Réaliser la construction suivante.
2. Les points \text {R} , \text {I} et \text {X} sont-ils alignés ? Justifier.
- Construire le segment \text {[BI]} de longueur 4~\text{cm.}
- Placer \text {S} sur la demi-droite \text {[BI)} tel que \widehat{\mathrm{BIS}} soit un angle plat.
- Construire l'angle \widehat{\mathrm{SIX}} de mesure 32^\circ.
- Construire l'angle \widehat{\mathrm{SIR}} de mesure 148^\circ.
Cliquez pour accéder à GeoGebra
2. Les points \text {R} , \text {I} et \text {X} sont-ils alignés ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
73
1. Réaliser la construction suivante.
2. Déterminer les mesures de \widehat{\text {BAD}} et \widehat{\text {CAD}}.
3. Si on modifie la position du point \text {B} sur la
droite \text {(AB)} , la mesure de ces angles change-t-elle ? Justifier.
- Tracer une droite \text {(AB)} .
- Construire l'angle \widehat{\text {BAC}} tel que \widehat{\mathrm{BAC}}=78^{\circ}.
- Tracer la bissectrice de cet angle et placer un point \text {D} sur cette demi-droite.
Cliquez pour accéder à GeoGebra
2. Déterminer les mesures de \widehat{\text {BAD}} et \widehat{\text {CAD}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
74
Sur cette figure, les droites \text {(AD)} et \text {(BC)}
se coupent en \text {O} . On définit \text {E} et \text {F} tels que
\text {[OE)} est la bissectrice de \widehat{\text {DOC}} et \text {[OF)} est
celle de \widehat{\text {AOB}}. Démontrer que les points \text {B} , \text {O}
et \text {F} sont alignés.

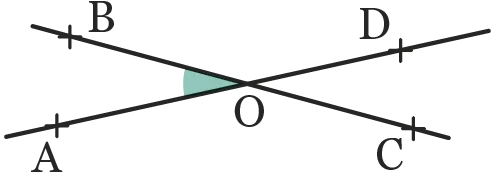


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
75
On a commencé
à tracer une fleur
formée de pétales
identiques.
Chaque pétale est séparé du suivant par un angle toujours identique.

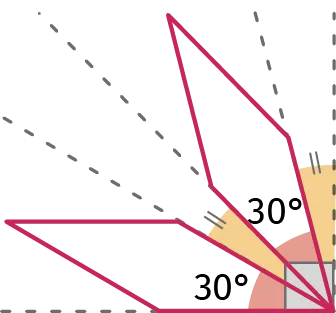
1. À partir de la figure ci-dessus, déterminer la mesure d'un de ces angles.
2. Chaque pétale est modélisé par un losange
de côté 3~\mathrm{cm}. Réaliser la figure complète.
Chaque pétale est séparé du suivant par un angle toujours identique.


1. À partir de la figure ci-dessus, déterminer la mesure d'un de ces angles.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
76
Au VIe siècle avant notre ère, les Grecs ont
construit un tunnel sur l'île de Samos. Ils ont
creusé par les deux côtés en même temps
sur une distance de 1~\mathrm{km} et se sont trompés
de 60~\mathrm{cm} seulement !
1. Pour faire un plan, on appelle \text {A} et \text {B} les deux entrées du tunnel de Samos. On peut relier \text {A} et \text {B} par deux segments \text {[AC]} et \text {[CB]} qui contournent la montagne et tels que \mathrm{AC}=0,9 \mathrm{~km}, \mathrm{CB}=1,1 \mathrm{~km} et \widehat{\mathrm{ACB}}=59^{\circ}.
Construire un schéma à l'échelle où 10~\mathrm{cm} sur le dessin représentent 1~\mathrm{km} dans la réalité.
2. Vérifier que le tunnel mesure bien environ
1~\mathrm{km}.
3. Mesurer les angles \widehat{\text {CBA}} et \widehat{\text {CAB}} pour
savoir dans quelles directions creuser.
1. Pour faire un plan, on appelle \text {A} et \text {B} les deux entrées du tunnel de Samos. On peut relier \text {A} et \text {B} par deux segments \text {[AC]} et \text {[CB]} qui contournent la montagne et tels que \mathrm{AC}=0,9 \mathrm{~km}, \mathrm{CB}=1,1 \mathrm{~km} et \widehat{\mathrm{ACB}}=59^{\circ}.
Construire un schéma à l'échelle où 10~\mathrm{cm} sur le dessin représentent 1~\mathrm{km} dans la réalité.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Club de maths
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
77
Comment tracer la bissectrice
d'un angle en n'utilisant qu'un
compas et une règle non graduée ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
78
Quel est l'angle formé par la petite et la grande aiguille d'une horloge à 15 \text{h} 30 ? Et à 16 \text{h} 45 ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
79
Faire un nœud avec
une bande de papier de
2~\mathrm{cm} de large par 20~\mathrm{cm}
de long et l'aplatir pour
former un pentagone
régulier. En déduire un
gabarit des angles de
108^\circet de 36^\circ.








Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

