Cercles et disques

Lorsque l'on calcule la longueur d'un cercle, l'aire d'un disque ou le volume d'une boule, un nombre bien particulier apparaît dans la formule : π, prononcé « pi ». Cette constante, dont il n'existe pas de valeur décimale exacte, est égale au rapport entre la longueur du cercle et son diamètre. On l'appelle ainsi parce qu'il s'agit de la première lettre du mot \pi \varepsilon \rho і \mu \varepsilon т \rho о \varsigma, qui signifie « périmètre » en grec.

En 250 avant notre ère, Archimède, un grand savant grec, propose une méthode pour trouver une valeur approchée de π. L'idée est d'encadrer le cercle par deux polygones : un plus petit que le cercle et un plus grand, dont il sait mesurer le périmètre. En augmentant le nombre de côtés des polygones, ceux-ci sont de plus en plus rapprochés du cercle. Il peut alors obtenir un encadrement précis de la valeur de π.

Avec cette méthode et un polygone à 96 côtés, il obtient \frac{223}{71} \leqslant \pi \leqslant \frac{22}{7}.

Le cercle est l'un des symboles les plus répandus à travers le monde. Il est présent dans la nature et est utilisé par l'être humain. C'est par exemple le cas de la roue ou bien du jeu de fléchettes.

Une cible standard est un disque de 451\mathrm{~mm} de diamètre, divisé en vingt secteurs angulaires correspondant au nombre de points obtenus. Le centre du disque est appelé la bulle. On y retrouve également deux couronnes (surfaces délimitées par deux cercles) dont la largeur intérieure est de 8\mathrm{~mm}.

Le rayon du cercle extérieur de la couronne des doubles est de 170\mathrm{~mm}, et celui de la couronne des triples est de 107,4\mathrm{~mm}.

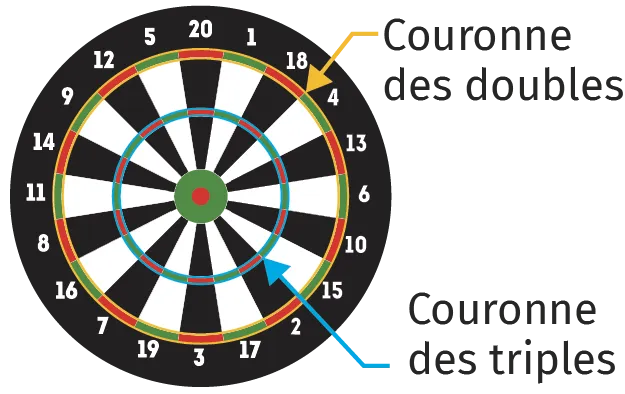
Un joueur a lancé une fléchette à 25\mathrm{~cm} du centre. A-t-elle atteint la cible ? Justifier.

Un pêcheur se trouve sur un rocher au milieu d'un lac. Il a avec lui une canne à pêche et un fil lui permettant de pêcher jusqu'à une distance de 15\mathrm{~m}.

1. Représenter le pêcheur par un point \mathrm{P}.
2. Représenter la zone dans laquelle il peut pêcher. On prendra comme échelle 1\mathrm{~cm} sur le dessin pour 3\mathrm{~m} dans la réalité.
Cette zone est appelée le disque de centre \mathrm{P} et de rayon 15\mathrm{~m}.

Bilan

À quelle condition un point appartient-il au disque de centre \mathrm{O} et de rayon r ?

Pour réaliser cette activité, utiliser

la fiche n°14

.
Dans cette activité, on utilise une bande de papier représentant le diamètre d'un cercle.

1. Pour chaque cercle, découper la bande de papier correspondante.
2. a. En prenant comme unité de longueur la bande de papier, mesurer la longueur de chacun des cercles.

b. Que peut-on constater ?

3. Sur le cahier, tracer un cercle de diamètre quelconque et réaliser la même manipulation que précédemment. La remarque précédente est-elle toujours valable ?

Bilan

Proposer une formule approximative pour calculer la longueur d'un cercle en fonction du diamètre puis en fonction du rayon.