Chapitre 14
Cours
Cercles et disques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Cercles
Définitions
Un cercle est l'ensemble de tous les points situés à une même
distance d'un même point appelé le centre. Cette distance est
appelée le rayon du cercle.
- Un rayon est un segment reliant le centre à un point du cercle.
- Un diamètre est un segment reliant deux points du cercle et passant par le centre du cercle.
- Une corde est un segment reliant deux points distincts du cercle.

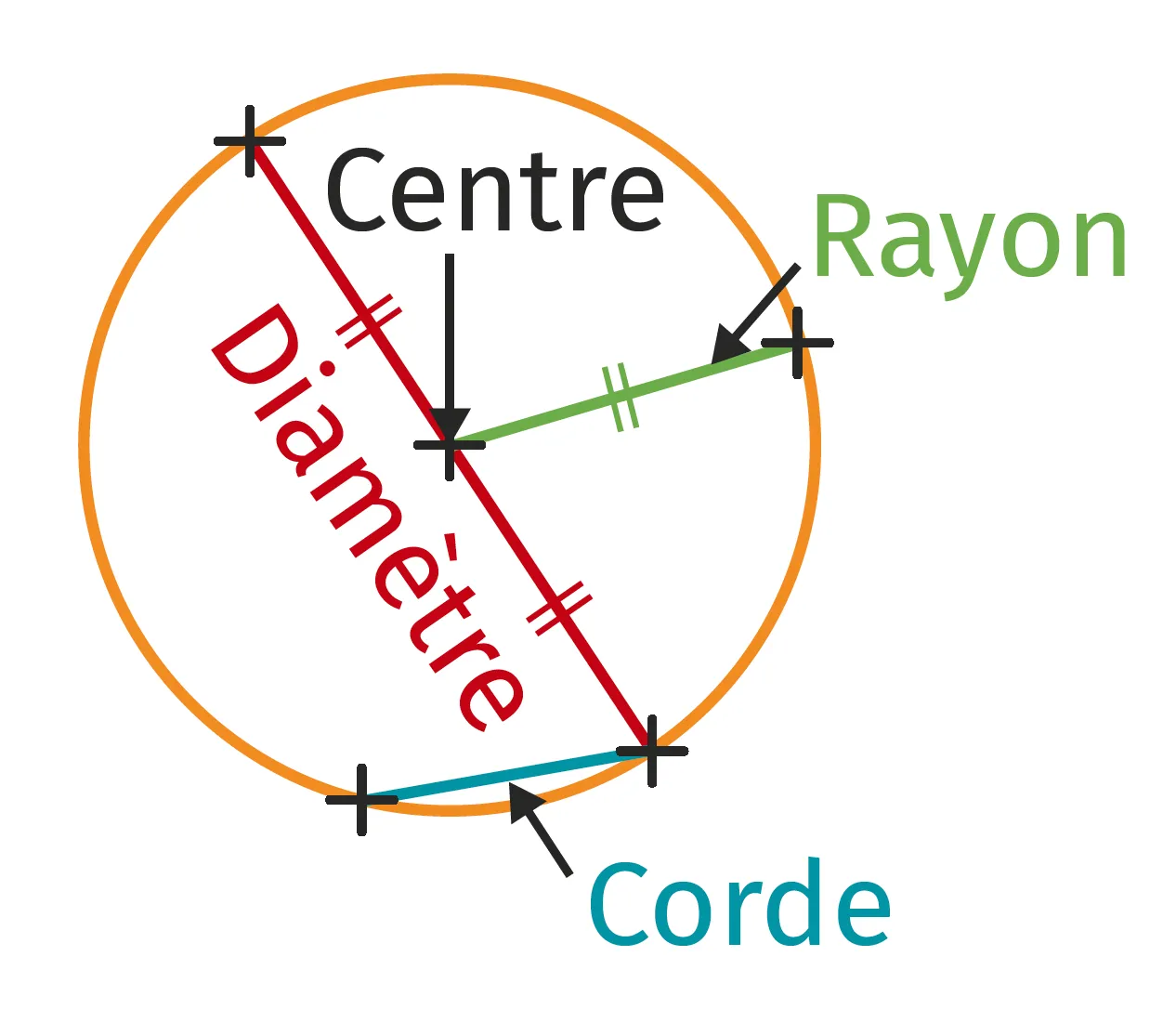
- Remarque : Les termes « rayon » et « diamètre » désignent à la fois un segment et une longueur.
Propriétés
- La longueur d'un diamètre correspond à deux fois celle du rayon. Elle est toujours supérieure ou égale à la longueur d'une corde.
- La longueur \mathrm{L} d'un cercle de diamètre \mathrm{D} est proportionnelle à son diamètre. Elle est égale à \mathrm{L}~= \pi~\times~\mathrm{D} ou encore \mathrm{L}~= 2~\times~\pi~\times~r où r représente le rayon.
- Le nombre \pi (qui se lit « pi ») n'est pas un nombre décimal et ne peut pas s'écrire sous la forme d'une fraction, il possède une infinité de décimales. On a \pi \approx 3,14.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Disques
Définition
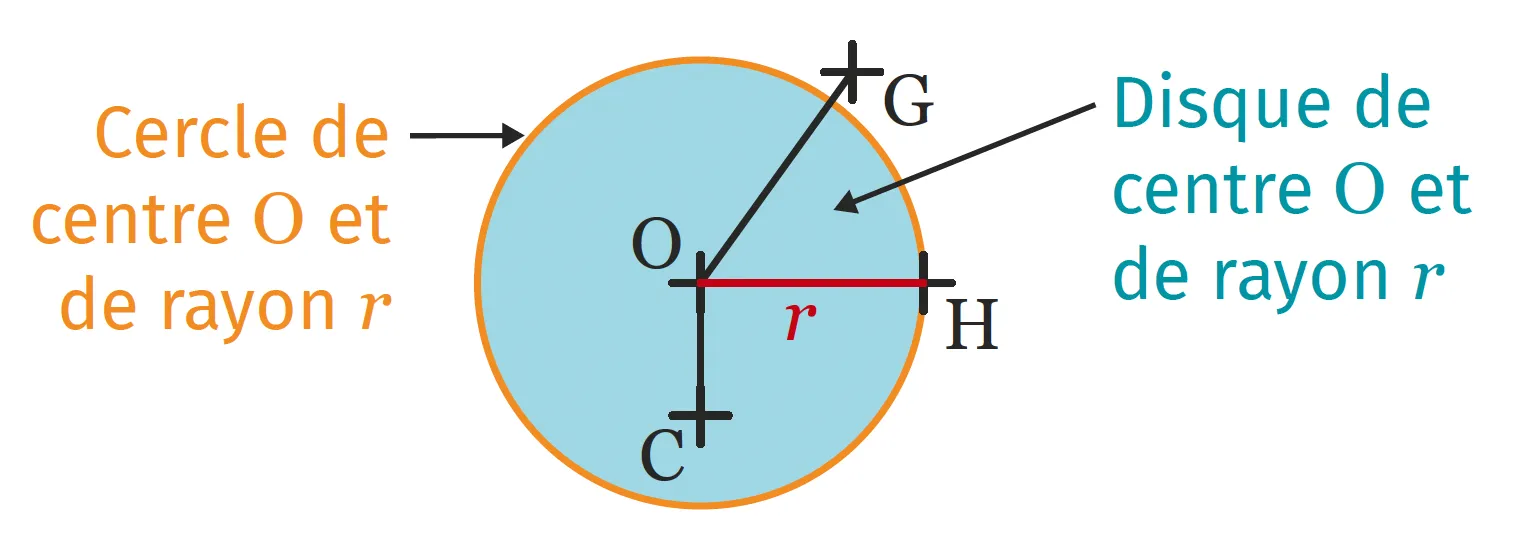
Le disque de centre \mathrm{O} et de rayon r est l'ensemble de tous les points situés à une distance de \mathrm{O} inférieure ou égale à r. Il s'agit de la surface délimitée par le cercle de même centre et de même rayon.
Exemple :
Les points \mathrm{C}, \mathrm{O} et \mathrm{H} appartiennent au disque de centre \mathrm{O} et de rayon r. Le point \mathrm{G} n'appartient pas au disque de centre \mathrm{O} et de rayon r donc \mathrm{OG}>r.
Les points \mathrm{C}, \mathrm{O} et \mathrm{H} appartiennent au disque de centre \mathrm{O} et de rayon r. Le point \mathrm{G} n'appartient pas au disque de centre \mathrm{O} et de rayon r donc \mathrm{OG}>r.

Version interactive
Propriété
Le périmètre \mathrm{P} d'un disque de diamètre \mathrm{D} est égal à la longueur du cercle délimitant ce disque. On a donc \mathrm{P}=~\pi~\times~\mathrm{D}= 2~\times~\pi~\times~r (où r est le rayon du disque).
Exemple :
Le périmètre d'un disque de rayon \color{red}5 cm vaut : \mathrm{P}=~2~\times~\pi~\times~{\color{red}5}~\mathrm{~cm}~\approx~31,4~\mathrm{~cm}.
Le périmètre d'un disque de rayon \color{red}5 cm vaut : \mathrm{P}=~2~\times~\pi~\times~{\color{red}5}~\mathrm{~cm}~\approx~31,4~\mathrm{~cm}.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille