Mathématiques 6e - 2025
Mes Pages
Rappels de primaire
Chapitre 1
Nombres entiers
Chapitre 2
Notion de fraction
Chapitre 3
Opérations sur les fractions
Chapitre 4
Nombres décimaux
Chapitre 5
Demi-droites graduées
Chapitre 6
Addition, soustraction, multiplication
Chapitre 7
Divisions
Chapitre 8
Organisation et gestion de données
Chapitre 9
Proportionnalité
Chapitre 10
Durées
Chapitre 11
Probabilités
Chapitre 12
Droites et segments
Chapitre 13
Angles
Chapitre 14
Cercles et disques
Chapitre 15
Symétrie axiale
Chapitre 16
Triangles
Chapitre 17
Aires et volumes
Outils numériques
Chapitre 16
Entrée en matière
Triangles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Histoire des mathsPoints remarquables des triangles
Les triangles possèdent de nombreux points remarquables,
parfois aussi appelés centres du triangle.
Les mathématiciens de la Grèce antique étaient déjà familiers avec certains d'entre eux : le centre de gravité, le centre du cercle inscrit, l'orthocentre ou bien encore le centre du cercle circonscrit présenté dans ce chapitre.
Les siècles suivants, le point de Torricelli (en 1636), le point de Vecten (en 1815) ou bien encore le point de Lemoine (en 1873) sont définis, mais ce n'est que dans les années 1980 qu'une définition claire et précise d'un centre du triangle a été énoncée.
Au 7 octobre 2024, l'Encyclopédie des centres du triangle du mathématicien américain Clark Kimberling recensait pas moins de 65 607 points !
Les mathématiciens de la Grèce antique étaient déjà familiers avec certains d'entre eux : le centre de gravité, le centre du cercle inscrit, l'orthocentre ou bien encore le centre du cercle circonscrit présenté dans ce chapitre.
Les siècles suivants, le point de Torricelli (en 1636), le point de Vecten (en 1815) ou bien encore le point de Lemoine (en 1873) sont définis, mais ce n'est que dans les années 1980 qu'une définition claire et précise d'un centre du triangle a été énoncée.
Au 7 octobre 2024, l'Encyclopédie des centres du triangle du mathématicien américain Clark Kimberling recensait pas moins de 65 607 points !
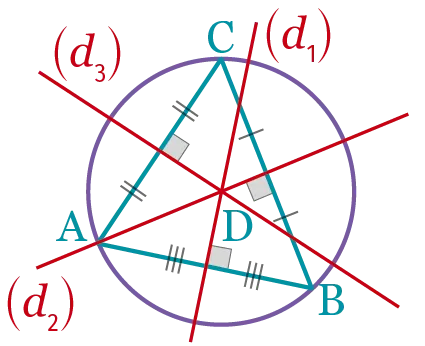
Centre du cercle circonscrit.
Dans un triangle non équilatéral, tracer précisément les bissectrices des trois angles
et les médiatrices des trois côtés. Que remarque-t-on ? Que se passe-t-il dans un
triangle équilatéral ?
Supplément numérique
Retrouvez cette histoire en .
Cliquez pour accéder à GeoGebra
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les maths, à quoi ça sert ?
Pour localiser un téléphone portable, on
peut utiliser la méthode de la triangulation
GMS. Le réseau téléphonique est constitué de
bornes auxquelles se connectent à distance les
téléphones.
L'information que chaque borne peut donner est la distance qui la sépare d'un téléphone connecté. Ainsi, avec trois bornes, en croisant leurs informations, on peut déterminer la position exacte d'un téléphone.
L'information que chaque borne peut donner est la distance qui la sépare d'un téléphone connecté. Ainsi, avec trois bornes, en croisant leurs informations, on peut déterminer la position exacte d'un téléphone.
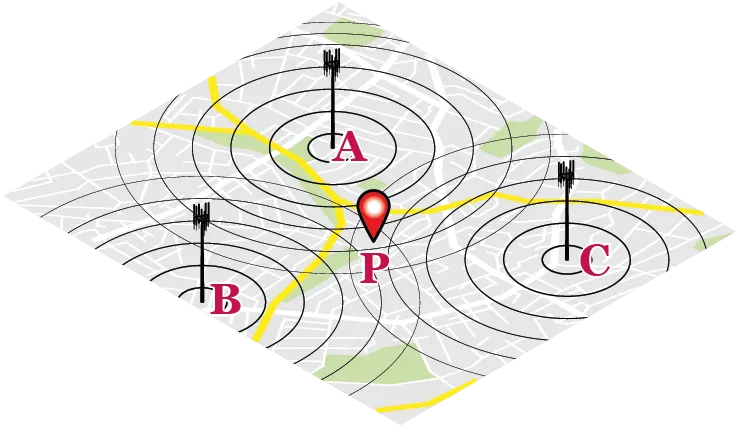
En utilisant un schéma, montrer que deux bornes ne sont pas suffisantes pour
donner la position exacte d'un téléphone alors qu'il n'y a pas de problème avec
trois bornes.
Supplément numérique
Une visualisation de .
Cliquez ici pour avoir accès à un espace de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 1Construire un triangle au compas
1. Réaliser le programme de construction suivant.
- Tracer un segment \mathrm{[AB]} de longueur 6 cm.
- Construire le cercle de centre \mathrm{A} et de rayon 4 cm.
- Construire le cercle de centre \mathrm{B} et de rayon 5 cm.
- Nommer \mathrm{C} l'un des deux points d'intersection des deux cercles.
- Tracer les segments \mathrm{[AC]} et \mathrm{[BC]}.
2.
Quelle est la nature de la figure ainsi construite ? Quelles sont ses
dimensions ?
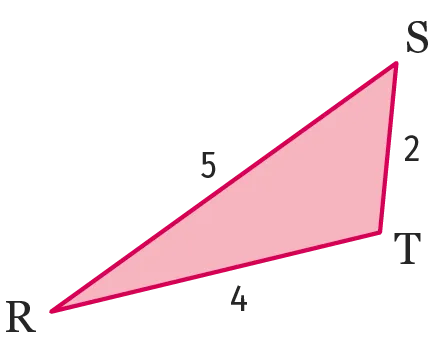
3.
Construire le triangle \mathrm{RST} dont les côtés mesurent 5 cm, 4 cm et
2 cm.
Quelles sont les étapes à suivre pour construire un triangle de longueurs données ?
Bilan
Quelles sont les étapes à suivre pour construire un triangle de longueurs données ?
Cliquez pour accéder à GeoGebra
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité de manipulationInégalité triangulaire
Pour réaliser cette activité, utiliser .
Le but de cette activité est de construire des triangles en utilisant la partie colorée des bandes.
1. En utilisant trois bandes, construire un triangle dont les côtés mesurent 10 cm, 8 cm et 6 cm. Existe-t-il plusieurs triangles différents ?
2. Construire trois autres triangles à l'aide des bandes en notant la longueur des côtés.
Le but de cette activité est de construire des triangles en utilisant la partie colorée des bandes.
1. En utilisant trois bandes, construire un triangle dont les côtés mesurent 10 cm, 8 cm et 6 cm. Existe-t-il plusieurs triangles différents ?
3. Que se passe-t-il si on essaie de construire un triangle avec les bandes de 8 cm, 5 cm et
3 cm ? Comment l'expliquer ?
4. Que se passe-t-il si on essaie de construire un triangle avec les bandes de 10 cm, 5 cm et
3 cm ? Comment l'expliquer ?
Quelle contrainte faut-il vérifier pour qu'un triangle soit constructible ?
Bilan
Quelle contrainte faut-il vérifier pour qu'un triangle soit constructible ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité de manipulationSomme des angles d'un triangle
1. Tracer un triangle quelconque sur une feuille de papier.
Coder les trois angles du triangle avec trois couleurs.
2. Tracer deux autres triangles strictement identiques et
coder les angles avec les mêmes couleurs.
Cliquez ici pour avoir accès à un espace de dessin
Cliquez ici pour avoir accès à un espace de dessin
3. Découper puis accoler les trois triangles comme sur le schéma ci-dessus.
Que peut-on dire des trois angles d'un triangle ? En déduire la valeur de la somme des angles d'un triangle.
Cliquez ici pour avoir accès à un espace de dessin
Bilan
Que peut-on dire des trois angles d'un triangle ? En déduire la valeur de la somme des angles d'un triangle.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
