Chapitre 16
Savoir-faire
Triangles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
MéthodeConstruire un triangle à l'aide
d'un compas et d'une règle graduée
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
Énoncé
Construire le triangle \mathrm{NEZ} tel que \mathrm{NE}=4 \mathrm{~cm}, \mathrm{EZ}=3,2 \mathrm{~cm} et \mathrm{NZ}=2,7 \mathrm{~cm}.Solution commentée

1

2
3
4
5
6
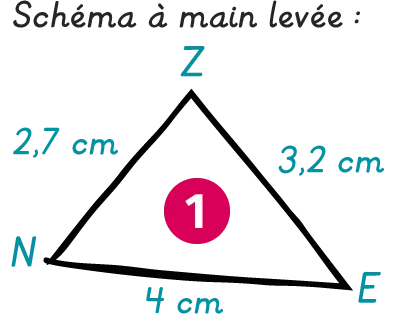
1. On commence par tracer un schéma complet à main levée.
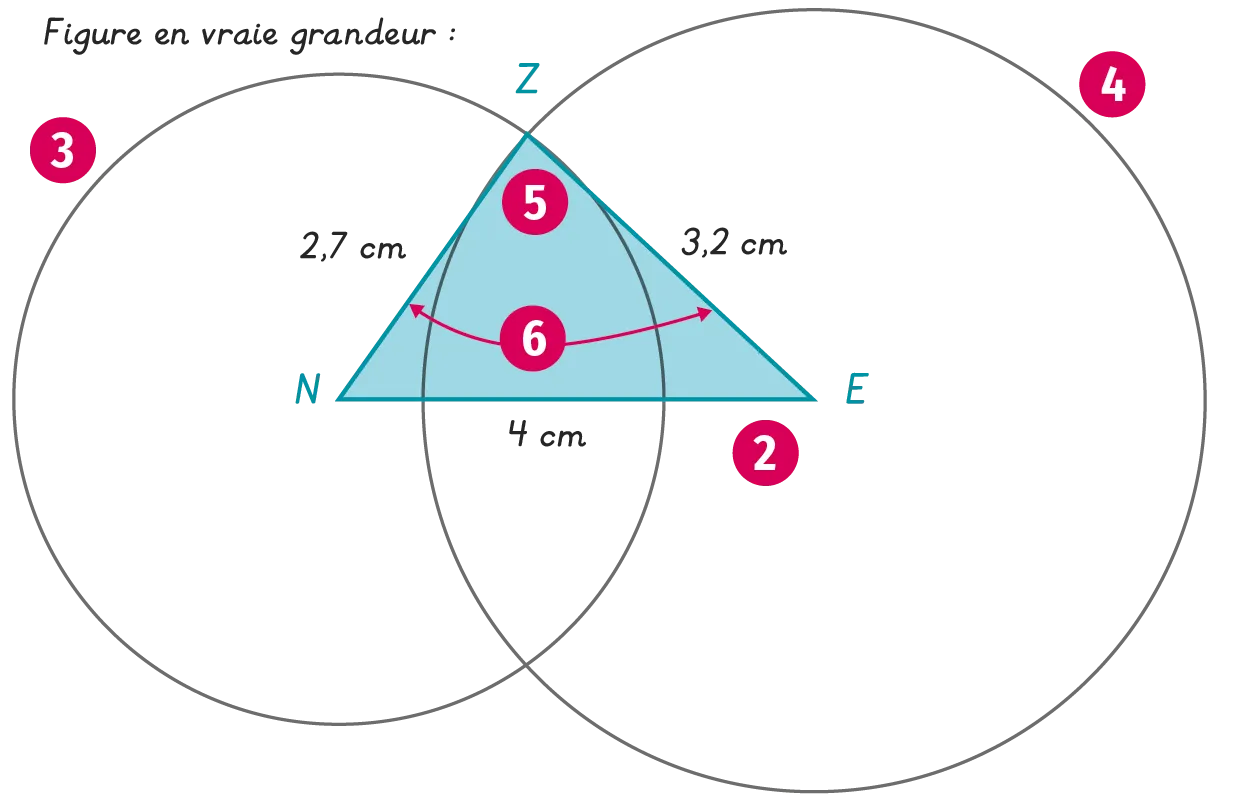
2. À l'aide d'une règle, on trace précisément un des trois côtés, par exemple le segment [\mathrm{NE}] de longueur 4 cm.
3. Le point \mathrm{Z} étant à 2,7 cm de \mathrm{N}, on trace le cercle de centre \mathrm{N} et de rayon 2,7 cm.
4. Le point \mathrm{Z} étant à 3,2 cm de \mathrm{E}, on trace le cercle de centre \mathrm{E} et de rayon 3,2 cm.
5. On nomme \mathrm{Z} l'un des deux points d'intersection des deux cercles.
6. On finit de construire le triangle en traçant les segments [\mathrm{NZ}] et [\mathrm{ZE}].
2. À l'aide d'une règle, on trace précisément un des trois côtés, par exemple le segment [\mathrm{NE}] de longueur 4 cm.
3. Le point \mathrm{Z} étant à 2,7 cm de \mathrm{N}, on trace le cercle de centre \mathrm{N} et de rayon 2,7 cm.
4. Le point \mathrm{Z} étant à 3,2 cm de \mathrm{E}, on trace le cercle de centre \mathrm{E} et de rayon 3,2 cm.
5. On nomme \mathrm{Z} l'un des deux points d'intersection des deux cercles.
6. On finit de construire le triangle en traçant les segments [\mathrm{NZ}] et [\mathrm{ZE}].
Remarque
À la place de tracer
les cercles complets, on peut tracer
uniquement les arcs de cercle pour
obtenir les points d'intersection.
Supplément numérique
La méthode .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
À mon tour
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
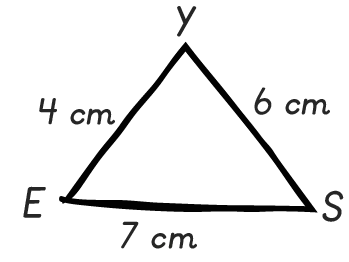
Construire le triangle suivant en vraie grandeur.

Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8
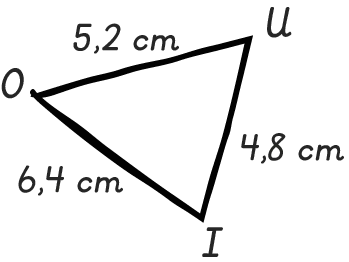
Construire le triangle suivant en vraie grandeur.

Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9
Construire le triangle \mathrm{FOU} tel que \mathrm{FO}=8 \mathrm{~cm}, \mathrm{OU}=6 \mathrm{~cm} et \mathrm{FU}=3 \mathrm{~cm}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10
Construire le triangle \mathrm{ROI} tel que \mathrm{RO}=5,8 \mathrm{~cm}, \mathrm{OI}=6,4 \mathrm{~cm} et \mathrm{RI}=7,3 \mathrm{~cm}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11
Construire le triangle \mathrm{DAM} isocèle en \mathrm{A} tel que \mathrm{AD}=64 \mathrm{~mm} et \mathrm{DM}=42 \mathrm{~mm}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12
Construire le triangle équilatéral \mathrm{CAV}
tel que \mathrm{AC}=4,6 \mathrm{~cm}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
MéthodeConstruire un triangle à l'aide d'un
rapporteur et d'une règle graduée
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13
Énoncé
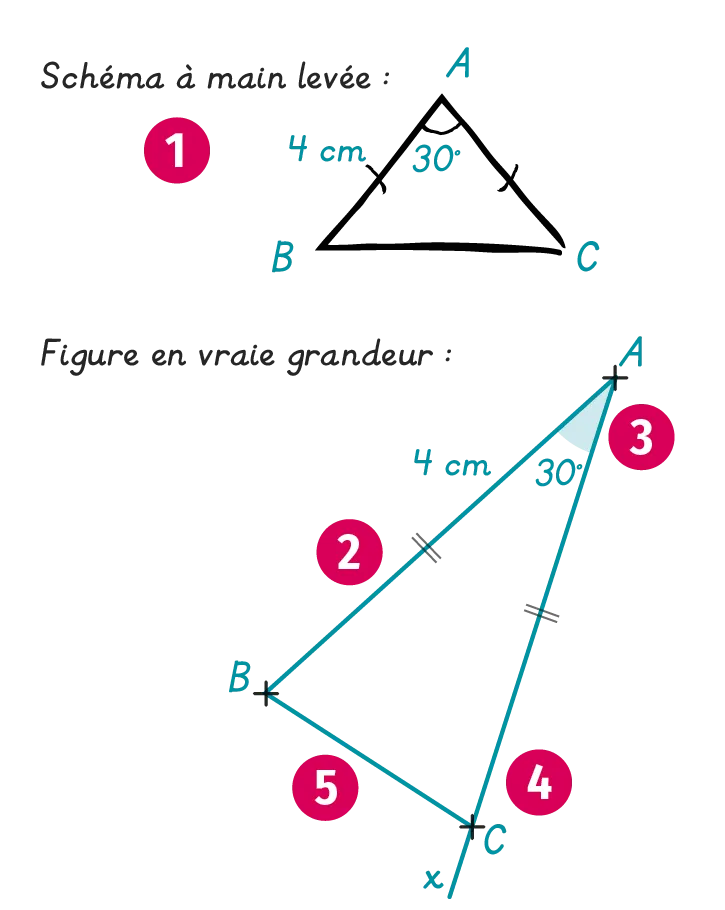
Construire le triangle \mathrm{ABC} isocèle en \mathrm{A}, sachant que \mathrm{AB}=4 \mathrm{~cm} et \widehat{\mathrm{BAC}}=30^{\circ}.Solution commentée

1
2
3
4
5
1. On commence par tracer un schéma complet
à main levée. On code les égalités de longueur
et d'angle dont on a besoin.
2. À l'aide d'une règle, on trace précisément un côté connu. Ici, on trace le segment [\mathrm{AB}] de longueur 4 cm.
3. À l'aide du rapporteur on trace une demi-droite [\mathrm{Ax}) de manière à tracer un angle de sommet \mathrm{A} et de mesure 30^{\circ}.
4. Le triangle étant isocèle en \mathrm{A}, le segment [\mathrm{AC}] mesure aussi 4 cm : on peut donc placer le point \mathrm{C}.
5. On trace le segment [\mathrm{BC}] afin de finir de tracer le triangle \mathrm{ABC}.
2. À l'aide d'une règle, on trace précisément un côté connu. Ici, on trace le segment [\mathrm{AB}] de longueur 4 cm.
3. À l'aide du rapporteur on trace une demi-droite [\mathrm{Ax}) de manière à tracer un angle de sommet \mathrm{A} et de mesure 30^{\circ}.
4. Le triangle étant isocèle en \mathrm{A}, le segment [\mathrm{AC}] mesure aussi 4 cm : on peut donc placer le point \mathrm{C}.
5. On trace le segment [\mathrm{BC}] afin de finir de tracer le triangle \mathrm{ABC}.
Supplément numérique
La méthode .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
À mon tour
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
14
Construire le triangle \mathrm{FER} isocèle en \mathrm{E}
tel que \mathrm{FE}=5 \mathrm{~cm} et \widehat{\mathrm{FER}}=120^{\circ}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15

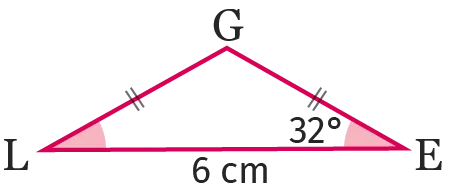
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16
Construire le triangle \mathrm{VAR} isocèle en \mathrm{R}
tel que \mathrm{VR}=6 \mathrm{~cm} et \widehat{\mathrm{VRA}}=43^{\circ}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17
Construire le triangle \mathrm{VAR} isocèle en \mathrm{A}
tel que \mathrm{VR}=6 \mathrm{~cm} et \widehat{\mathrm{VRA}}=43^{\circ}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18
Construire le triangle suivant.

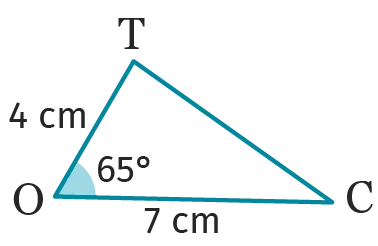
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19
Construire le triangle \mathrm{PLI}
tel que \mathrm{PI}=4 \mathrm{~cm}, \mathrm{LI}=5 \mathrm{~cm} et \widehat{\mathrm{PIL}}=50^{\circ}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20
Construire le triangle \mathrm{SAC}
tel que \mathrm{SA}=6,4 \mathrm{~cm}, \mathrm{AC}=5,3 \mathrm{~cm} et \widehat{\mathrm{CAS}}=110^{\circ}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21
Construire le triangle \mathrm{VOL}
tel que \mathrm{VO}=6,5 \mathrm{~cm}, \mathrm{OL}=5,2 \mathrm{~cm} et \widehat{\mathrm{VOL}}=40^{\circ}.
Cliquez pour accéder à GeoGebra
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

