Mathématiques 6e - 2025
Mes Pages
Chapitre 1
Nombres entiers
Chapitre 2
Notion de fraction
Chapitre 3
Opérations sur les fractions
Chapitre 4
Nombres décimaux
Chapitre 5
Demi-droites graduées
Chapitre 6
Addition, soustraction, multiplication
Chapitre 7
Divisions
Chapitre 8
Organisation et gestion de données
Chapitre 9
Proportionnalité
Chapitre 10
Durées
Chapitre 11
Probabilités
Chapitre 12
Droites et segments
Chapitre 13
Angles
Chapitre 14
Cercles et disques
Chapitre 15
Symétrie axiale
Chapitre 16
Triangles
Chapitre 17
Aires et volumes
Outils numériques
Chapitre 16
Entraînement
Triangles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Généralités sur les triangles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22
À l'oral
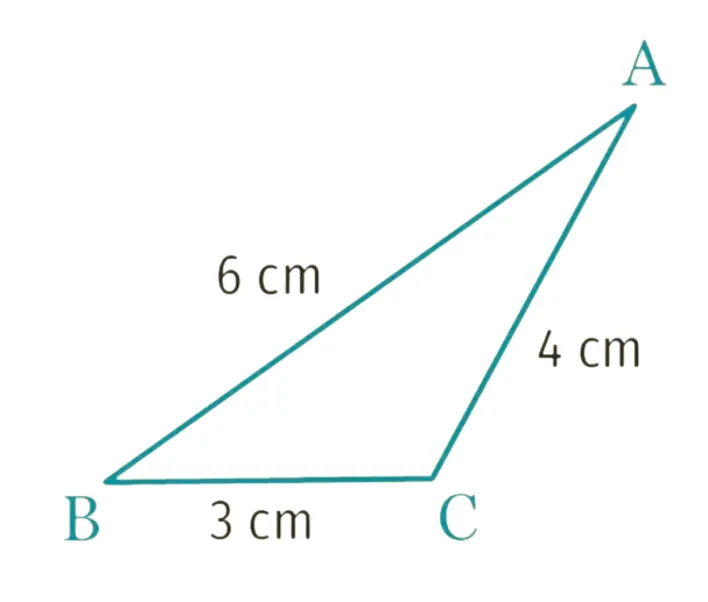
1. Quelle est la longueur du segment [\mathrm{AB}] ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
À l'oral
Dans chacun des cas suivants, dire
s'il est possible de construire le triangle
\mathrm{ABC}.
1. \mathrm{AB}=5 \mathrm{~cm} ; \mathrm{BC}=3 \mathrm{~cm} ; \mathrm{AC}=4 \mathrm{~cm}
2. \mathrm{AB}=6 \mathrm{~cm} ; \mathrm{BC}=6 \mathrm{~cm} ; \mathrm{AC}=6 \mathrm{~cm}
3. \mathrm{AB}=3 \mathrm{~cm} ; \mathrm{BC}=3 \mathrm{~cm} ; \mathrm{AC}=9 \mathrm{~cm}
4. \mathrm{AB}=4 \mathrm{~cm} ; \mathrm{BC}=5 \mathrm{~cm} ; \mathrm{AC}=0,5 \mathrm{~cm}
1. \mathrm{AB}=5 \mathrm{~cm} ; \mathrm{BC}=3 \mathrm{~cm} ; \mathrm{AC}=4 \mathrm{~cm}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
1. Ranger ces quatre étapes de
construction dans l'ordre chronologique.
2. Décrire par une phrase chaque étape.
2. Décrire par une phrase chaque étape.
a.
b.
b.
c.
d.
d.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25
Bilel trace le schéma à main levée
suivant.
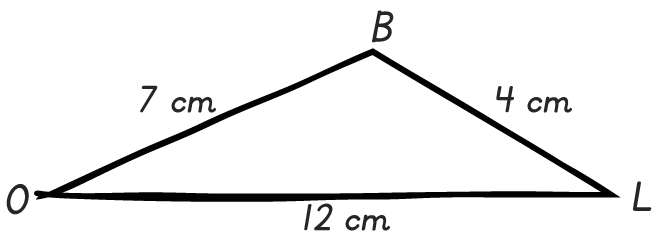Eve lui dit : « Tu n'arriveras jamais à
construire ce triangle en vraie grandeur. »
Pourquoi Eve peut-elle affirmer cela ?
Pourquoi Eve peut-elle affirmer cela ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26
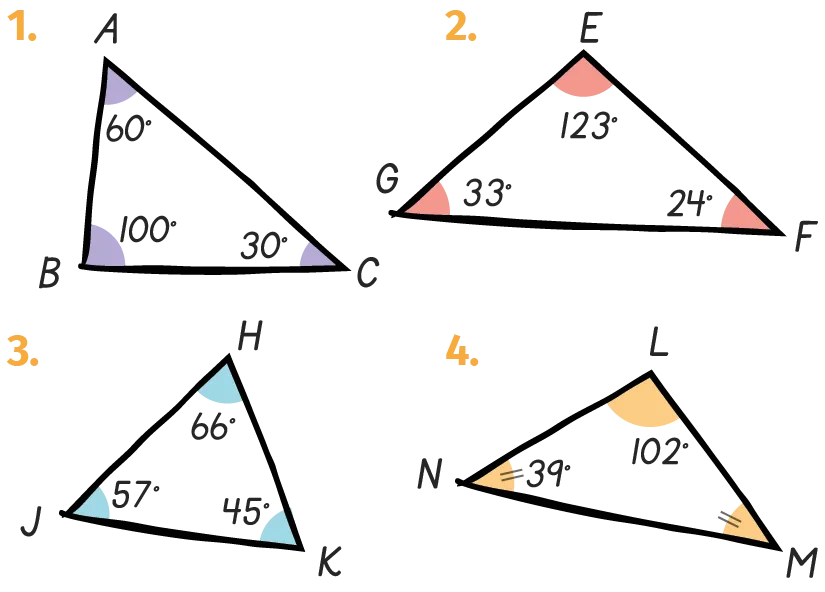
On considère le triangle \mathrm{ABC}. Recopier
et compléter le tableau suivant avec les
mesures d'angles manquantes.
| \widehat{\mathrm{ABC}} | \widehat{\mathrm{CBA}} | \widehat{\mathrm{ACB}} |
|---|---|---|
42^{\circ} | 67^{\circ} | |
24^{\circ} | 110^{\circ} | |
78^{\circ} | 53^{\circ} | |
39^{\circ} | 107^{\circ} |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27
Générateur d'exercices
Les triangles suivants sont dessinés à
main levée. Est-il possible de les construire ?
Justifier.
Triangle 1
Triangle 2
Triangle 3
Triangle 4
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28
Sophie demande à sa mère : « Est-ce
que tu peux me tracer un triangle avec deux
angles droits ? ».
Sa maman lui répond que c'est impossible. Pourquoi ?
Sa maman lui répond que c'est impossible. Pourquoi ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29
Dans le triangle \mathrm{NEZ} les angles \widehat{\mathrm{NEZ}}
et \widehat{\mathrm{NZE}} mesurent respectivement 53^{\circ} et 76^{\circ}.
Quelle est la mesure de l'angle \widehat{\mathrm{ENZ}} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30
Les points \mathrm{ A}, \mathrm{B} et \mathrm{D} sont-ils alignés ? Justifier.
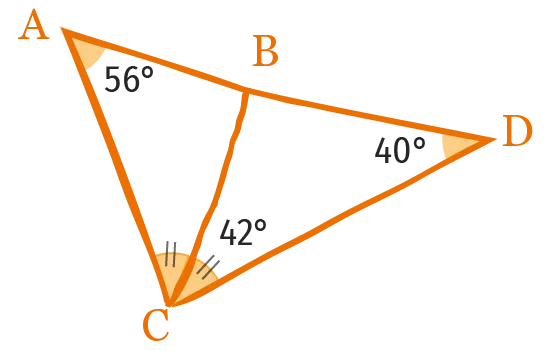
Ressource affichée de l'autre côté.
Faites d éfiler pour voir la suite.
Faites d éfiler pour voir la suite.
31
Construire les triangles suivants en vraie
grandeur.
1.
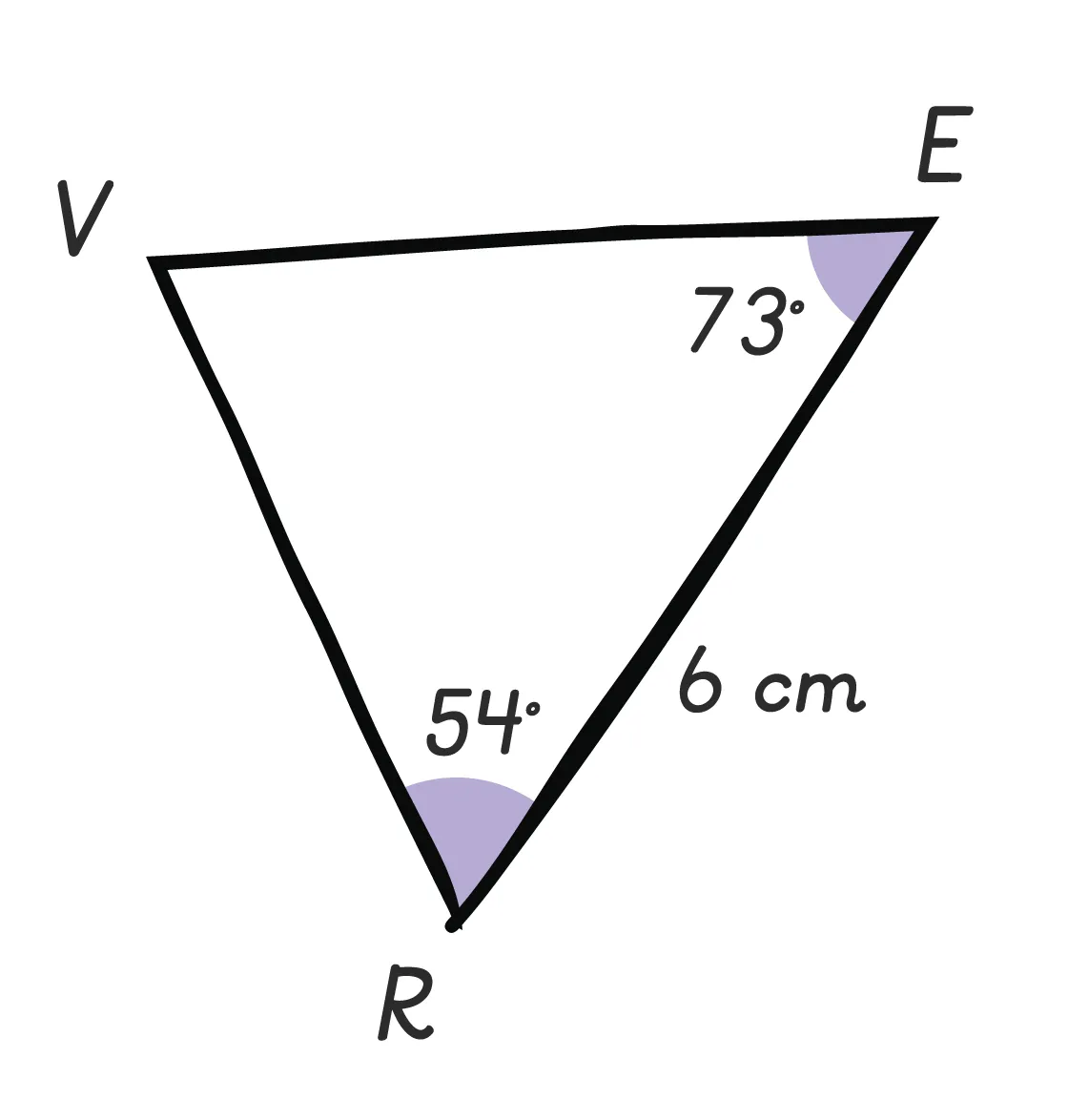
2.
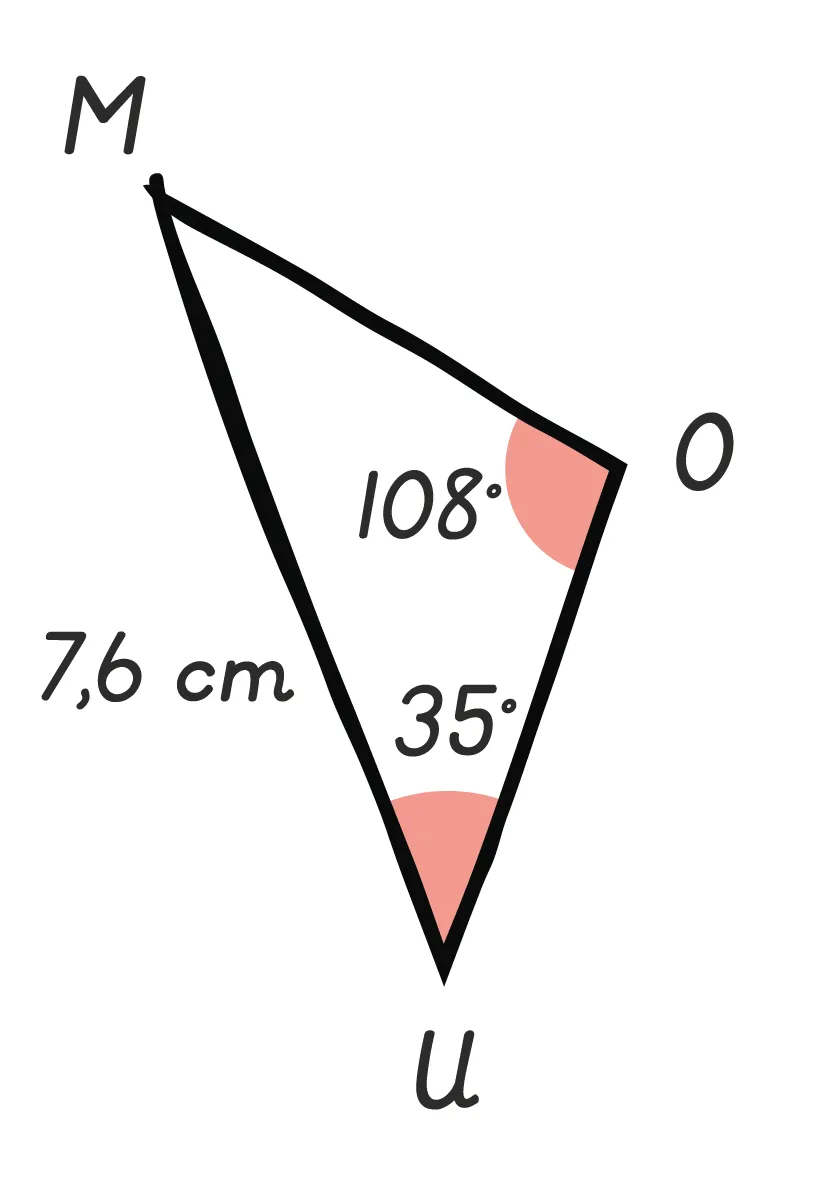
Cliquez pour accéder à GeoGebra
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32
1. Construire en vraie grandeur
le triangle \mathrm{JUS} tel que \mathrm{JU}=45 \mathrm{~mm},
\mathrm{US}=83 \mathrm{~mm} et \mathrm{JS}=59 \mathrm{~mm}.
2. Construire en vraie grandeur le triangle \mathrm{EAU} tel que \mathrm{EA}=7 \mathrm{~cm}, \mathrm{AC}=6,5 \mathrm{~cm} et \widehat{\mathrm{EAC}}=96^{\circ}.
3. Construire en vraie grandeur le triangle \mathrm{THE} tel que \mathrm{TH}=6,1 \mathrm{~cm}, \widehat{\mathrm{THE}}=36^{\circ} et \widehat{\mathrm{HTE}}=87^{\circ}.
2. Construire en vraie grandeur le triangle \mathrm{EAU} tel que \mathrm{EA}=7 \mathrm{~cm}, \mathrm{AC}=6,5 \mathrm{~cm} et \widehat{\mathrm{EAC}}=96^{\circ}.
3. Construire en vraie grandeur le triangle \mathrm{THE} tel que \mathrm{TH}=6,1 \mathrm{~cm}, \widehat{\mathrm{THE}}=36^{\circ} et \widehat{\mathrm{HTE}}=87^{\circ}.
Cliquez pour accéder à GeoGebra
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33
1. Construire le triangle \mathrm{PUR} tel que \mathrm{PU}=4,6 \mathrm{~cm},
\mathrm{UR}=7,2 \mathrm{~cm} et \mathrm{PR}=6,4 \mathrm{~cm}.
2. Tracer les médiatrices du triangle \mathrm{PUR}.
3. Tracer le cercle circonscrit au triangle \mathrm{PUR}.
2. Tracer les médiatrices du triangle \mathrm{PUR}.
3. Tracer le cercle circonscrit au triangle \mathrm{PUR}.
Cliquez pour accéder à GeoGebra
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
34
Pour chaque figure ci-après, dire en
justifiant si le cercle de centre \mathrm{D} est le cercle
circonscrit au triangle \mathrm{ABC}.
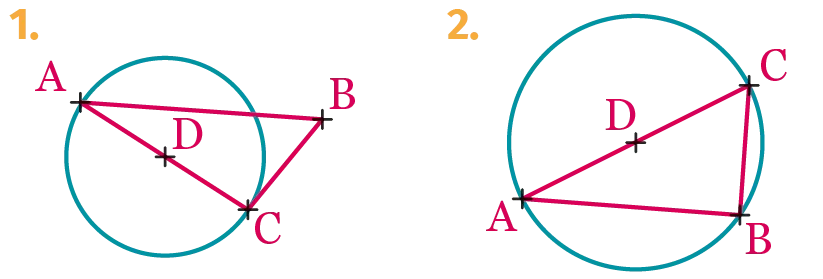
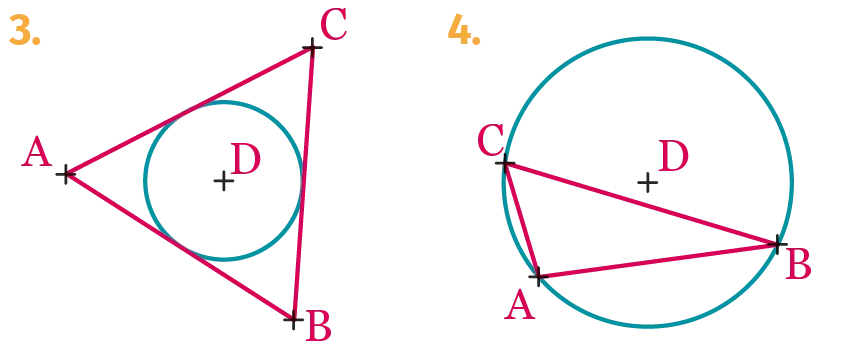
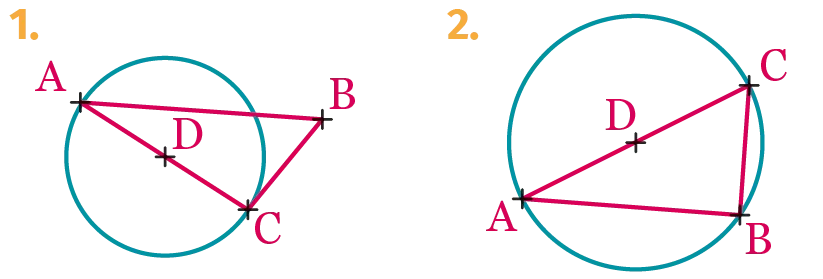
Figure 1
Figure 2
Figure 3
Figure 4
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35
On considère le triangle \mathrm{ABC}
ci-dessous. Le point \mathrm{D} est le point
d'intersection des droites \left(d_1\right), \left(d_2\right) et \left(d_1\right).
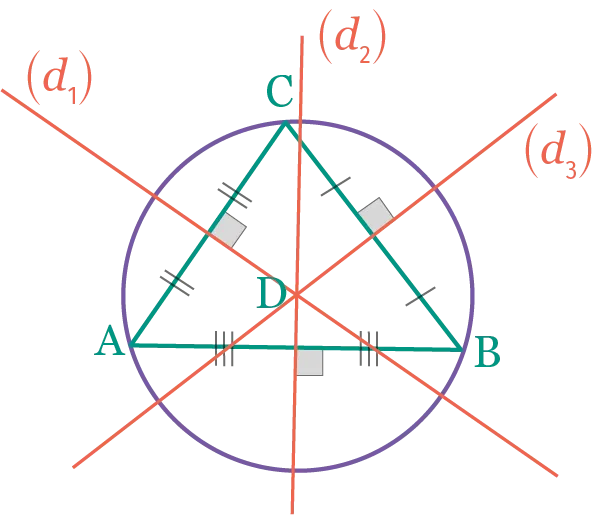
Que peut-on dire du cercle de centre \mathrm{D} passant par \mathrm{A} ? Justifier.
Que peut-on dire du cercle de centre \mathrm{D} passant par \mathrm{A} ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
36
Un château d'eau doit être construit à
égale distance de trois villages schématisés
ci-dessous par les points \mathrm{X}, \mathrm{Y} et \mathrm{Z}.
Reproduire la figure et placer précisément le château d'eau.
Reproduire la figure et placer précisément le château d'eau.
Cliquez ici pour avoir accès à un espace de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
37
TICE
1. En utilisant GeoGebra, construire un
triangle \mathrm{ABC} non plat et afficher la mesure
de chacun de ses angles.
2. Construire le cercle circonscrit au triangle \mathrm{ABC}.
3. Tester plusieurs positions du point \mathrm{A}. Dans quelles situations le centre du cercle circonscrit semble être à l'extérieur du triangle ? À l'intérieur ? Sur un côté ?
2. Construire le cercle circonscrit au triangle \mathrm{ABC}.
Cliquez pour accéder à GeoGebra
GeoGebra
3. Tester plusieurs positions du point \mathrm{A}. Dans quelles situations le centre du cercle circonscrit semble être à l'extérieur du triangle ? À l'intérieur ? Sur un côté ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Triangles rectangles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
38
À l'oral
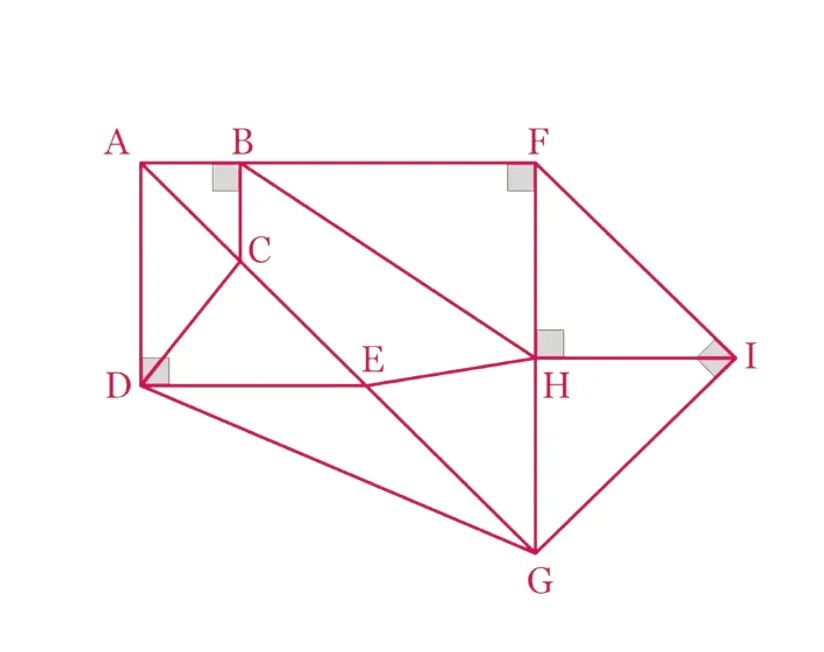
Les points \mathrm{A}, \mathrm{C}, \mathrm{E} et \mathrm{G} sont alignés ainsi que \mathrm{F}, \mathrm{H} et \mathrm{G}. À l'aide des codages, citer tous les triangles rectangles représentés sur cette figure.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
39
À l'oral
1. Dans le triangle \mathrm{RIZ} rectangle en
R, quel côté est l'hypoténuse ?
2. Dans le triangle \mathrm{TOP} rectangle en \mathrm{P},
quel est le nom de l'angle droit ?
3. Dans le triangle \mathrm{KIF} rectangle en \mathrm{F},
quel est le plus long côté ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
40
Pour éviter que la porte de sa salle de
classe ne claque, une enseignante décide
de fabriquer une petite cale. Pour cela, elle
découpe un morceau de bois dont une face
est un triangle rectangle.
Dans ce triangle, les deux côtés de l'angle droit mesurent 6 cm et 3 cm. Représenter cette face en vraie grandeur.
Dans ce triangle, les deux côtés de l'angle droit mesurent 6 cm et 3 cm. Représenter cette face en vraie grandeur.
Cliquez pour accéder à GeoGebra
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
41
Les deux triangles ci-dessous sont des
triangles rectangles. Déterminer la mesure
des angles manquants.
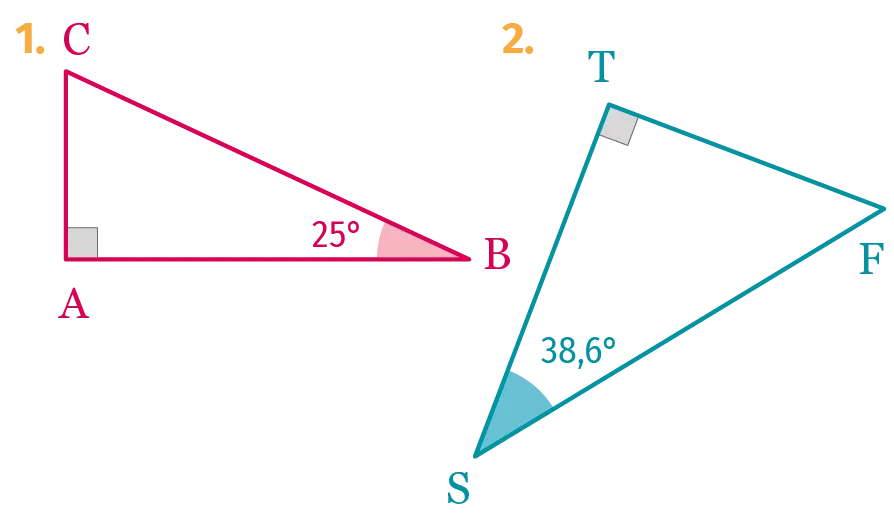
Triangle 1
Triangle 2
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
42
Générateur d'exercices
Dans le triangle \mathrm{OUI} rectangle en \mathrm{U},
l'angle \widehat{\mathrm{IOU}} mesure 72^{\circ}.
Calculer la mesure de l'angle \widehat{\mathrm{OIU}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
43
Dans le triangle \mathrm{YES} rectangle en \mathrm{S},
l'angle \widehat{\mathrm{YES}} mesure 34^{\circ}.
Calculer la mesure de l'angle \widehat{\mathrm{SYE}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
44
Dans le triangle \mathrm{IVA} rectangle en \mathrm{V},
l'angle \widehat{\mathrm{IAV}} mesure 18,73^{\circ}.
Calculer la mesure de l'angle \widehat{\mathrm{VIA}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
45
Dans un triangle rectangle, le plus grand
angle aigu mesure le triple de l'autre angle
aigu. Déterminer la mesure des trois angles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46
Déterminer la mesure de tous les angles
du triangle \mathrm{MFT} ci-dessous sachant que
la demi-droite [\mathrm{MC}) est la bissectrice de
l'angle \widehat{\mathrm{FMT}}.
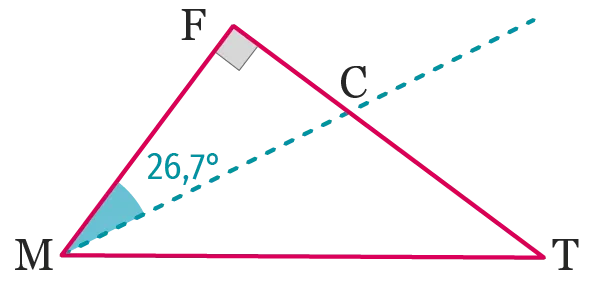
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Triangles isocèles et équilatéraux
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
47
À l'oral
Quel est le sommet principal du
triangle \mathrm{EAU} isocèle en \mathrm{U} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48
À l'oral
Quelle est la base du triangle \mathrm{THE}
isocèle en \mathrm{H} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49
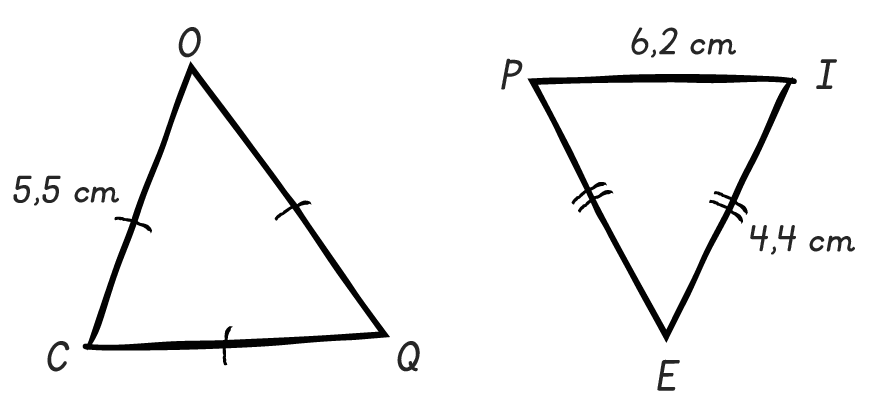
Donner, en justifiant, la nature de ces triangles, puis les construire en vraie grandeur.
Cliquez pour accéder à GeoGebra
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
50
Copie d'élève
Le professeur de Max lui demande
de tracer le triangle \mathrm{IPA} isocèle en \mathrm{P} tel que
\mathrm{PA}=6 \mathrm{~cm} et \mathrm{IA}=4 \mathrm{~cm}.
Voici la figure de Max.
Sa camarade Lia lui dit qu'il a fait une erreur. Expliquer quelle est cette erreur et construire la figure correcte.
Sa camarade Lia lui dit qu'il a fait une erreur. Expliquer quelle est cette erreur et construire la figure correcte.
Cliquez pour accéder à GeoGebra
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
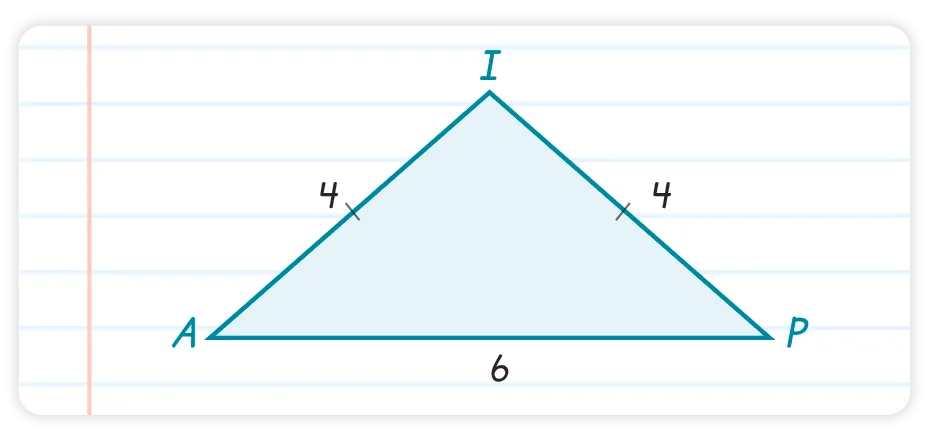
51
Les deux triangles ci-après sont des
triangles isocèles. Déterminer la mesure des
angles manquants.
Triangle 1
Triangle 2
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
52
Dans le triangle \mathrm{QUE} isocèle en \mathrm{E},
l'angle \widehat{\mathrm{EQU}} mesure 34,7^{\circ}.
Déterminer la mesure des deux autres angles
de ce triangle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
53
Générateur d'exercices
Dans le triangle \mathrm{QUE} isocèle en \mathrm{Q},
l'angle \widehat{\mathrm{EQU}} mesure 34,7^{\circ}.
Déterminer la mesure des deux autres angles
de ce triangle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
54
Exercice inversé
Donner la
consigne d'un
exercice dont la
solution serait de
tracer la figure suivante.
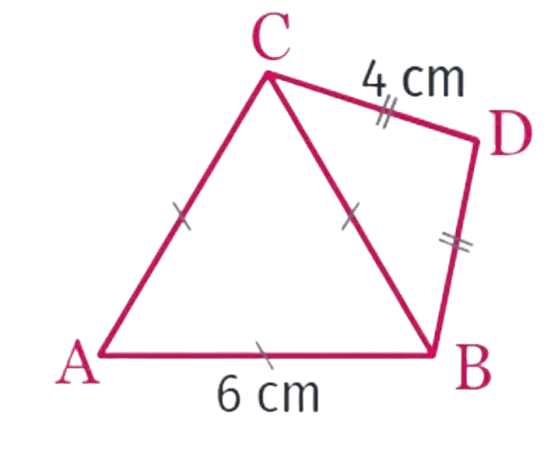
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
55
Environnement
Il est difficile d'observer
la Voie lactée en France
métropolitaine à cause de la
pollution lumineuse. Cependant, il existe
une zone, appelée le triangle noir du
Quercy, épargnée par les éclairages des
routes et des villes.
Les sommets de ce triangle sont les villes
de Livernon (L), Sauliac-sur-Célé (S) et
Labastide-Murat (M). C'est un triangle
isocèle en S. La distance à vol d'oiseau
entre Livernon et Sauliac-sur-Célé est de
17,4 \mathrm{km} et celle entre Livernon et
Labastide-Murat est de 21,9 \mathrm{km}.
1. Faire un schéma à main levée du triangle noir du Quercy.
2. Calculer le périmètre du triangle.
1. Faire un schéma à main levée du triangle noir du Quercy.
Cliquez ici pour avoir accès à un espace de dessin
2. Calculer le périmètre du triangle.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
